Spannungsbezogene Verzweigungslastfaktoren
Für eine rein analytische Ermittlung des kritischen Lastfaktors eines Beulfeldes wird in [1] folgende Gleichung (Kap. 10, Gl. 10.6) angegeben:
Daraus ist erkennbar, dass neben den Spannungsverhältnissen auch die Verzweigungslastfaktoren getrennt für die einzelnen Spannungskomponenten ermittelt oder bekannt sein müssen. Diese kritischen Lastfaktoren können über eine Rückrechnung aus den kritischen Plattenbeulspannungen ermittelt werden. Auf die Ermittlung dieser wurde bereits in diesem Fachbeitrag eingegangen:
Für die einzelnen Spannungskomponenten ergeben sich dadurch nun folgende Beziehungen:
Dieses Vorgehen eignet sich besonders für unversteifte beziehungsweise längsversteifte Beulfelder, für die entsprechende Beulwerte aus [2] oder [3] entnommen werden können.
Hilfsmittel FEM-Berechnung
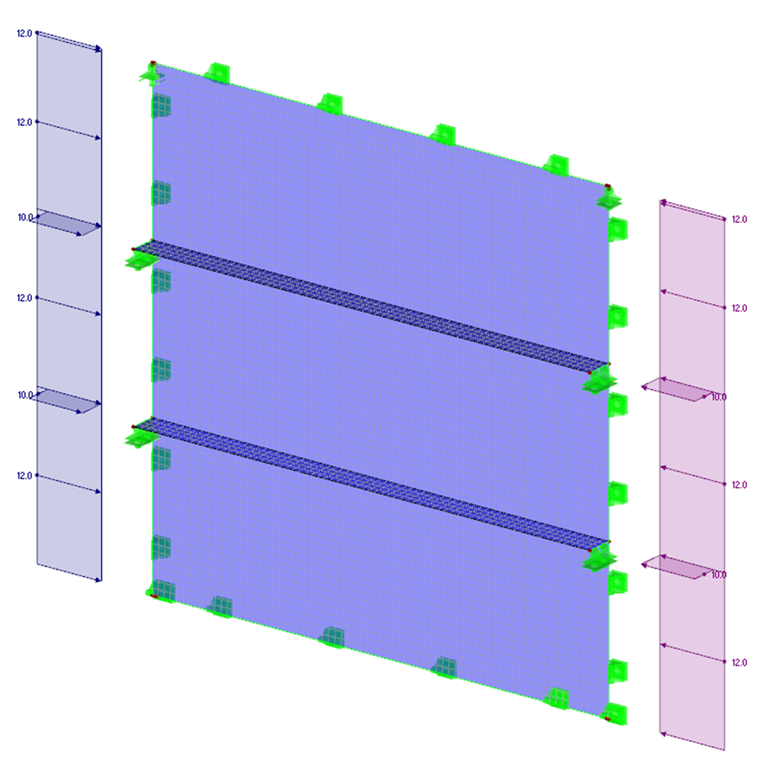
Sofern ein stark versteiftes Beulfeld mit Längs- und Quersteifen vorliegt, sollte die Ermittlung der Verzweigungslast am Gesamtsystem mittels FEM-Berechnung vorgenommen werden. Als Grundlage sollte hier ein Flächenmodell angestrebt werden und sämtliche Randbedingen (zum Beispiel Lagerung der Ränder, geometrische Lage und Belastung der Steifen sowie die Randspannungen) berücksichtigt werden. Für die Ermittlung nach LBA wird elastisches Materialverhalten angesetzt. Das folgende Beispiel zeigt die Modellierung eines längsversteiften Beulfeldes in RFEM.
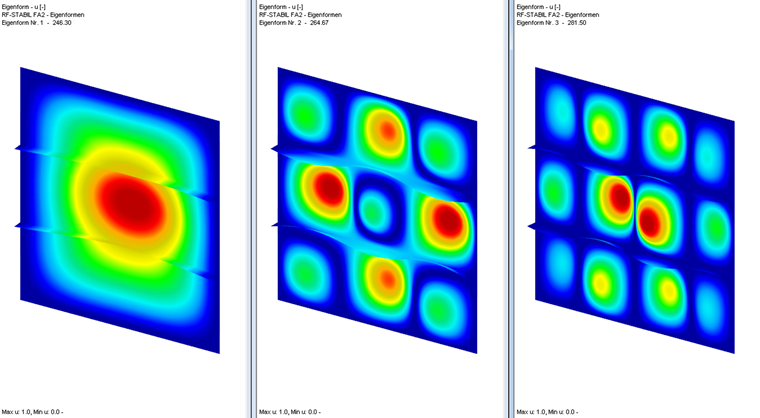
Für die Ermittlung des Verzweigungslastfaktors kommt das Zusatzmodul RF-STABIL zum Einsatz. Bei der Wahl der Eigenform ist auf ein globales Systemversagen zu achten.
Die 1. Eigenform in diesem Beispiel zeigt globales Beulen und ist daher als maßgebend anzusehen. In einigen Fällen können aber höhere Eigenformen bemessungsrelevant werden. Somit kann der Verzweigungslastfaktor sowohl für sämtliche Spannungskomponenten als auch getrennt (nur eine Spannungskomponente je Lastfall) berechnet werden.
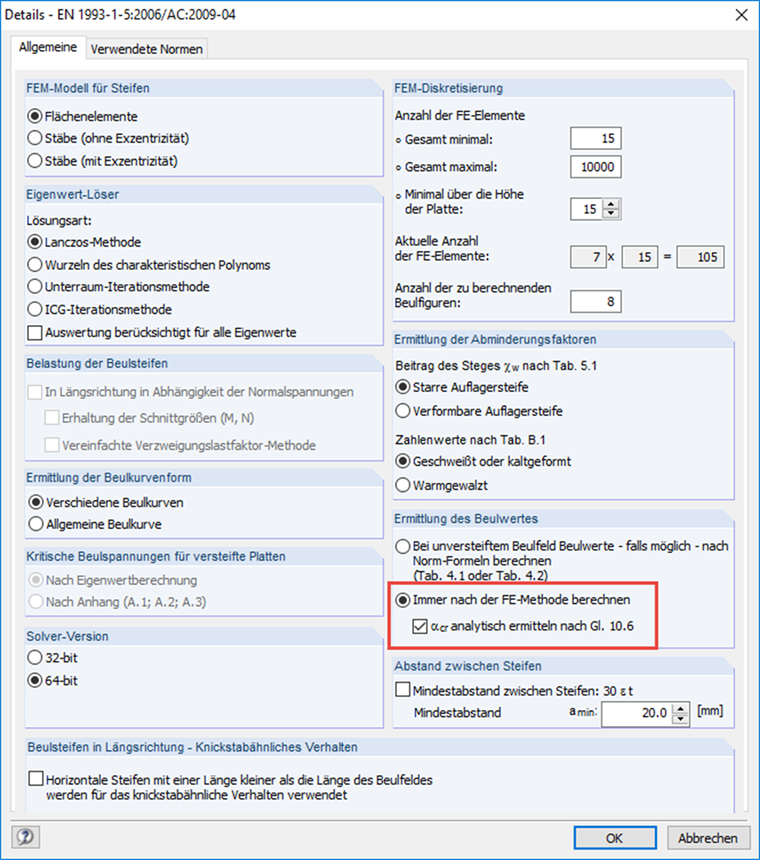
Einen vollständigen Beulnachweis nach der Methode der reduzierten Spannungen inklusive automatischer Eigenwertermittlung je Spannungskomponente bietet ebenfalls das Programm FE-BEUL.
Kritischer Lastfaktor im Beulnachweis
Es ergibt sich nun die Möglichkeit, entweder die einzelnen kritischen Lastfaktoren zu ermitteln und anschließend den gesamten Verzweigungslastfaktor mittels Gl. 10.6 aus [1] analytisch zu berechnen oder diesen direkt aus der FEM-Berechnung zu nutzen. In einigen Fällen ist die analytische Lösung als konservativ anzusehen. Daher bietet FE-BEUL optional folgende Auswahl.