7628x

001454

2017-06-19

Artykuł techniczny | Obliczanie współczynnika obciążenia krytycznego dla analizy wyboczenia liniowego

Analiza wyboczenia zgodnie z metodą szerokości efektywnej lub metodą zredukowanych naprężeń opiera się na określeniu obciążenia krytycznego układu, zwanej dalej LBA (liniowa analiza wyboczeniowa). W artykule tym wyjaśniono sposób obliczania współczynnika obciążenia krytycznego oraz zastosowanie metody elementów skończonych (MES).

Współczynniki obciążenia krytycznego odnoszące się do naprężeń

[1] udostępnia następujące równanie (s. 10, równ. 10.6) do czysto analitycznego wyznaczenia współczynnika obciążenia krytycznego panelu wyboczeniowego:

\frac{1}{α_{cr}} = \frac{1 ψ_{x}}{4 \cdot α_{cr, x}} \frac{1 ψ_{z}}{4 \cdot α_{cr, z}} {[{(\frac{1 ψ_{x}}{4 \cdot α_{cr, x}} \frac{1 ψ_{z}}{4 \cdot α_{cr, z}})}^{2} \frac{1 - ψ_{x}}{2 \cdot α_{cr, x}^{2}} \frac{1 - ψ_{z}}{2 \cdot α_{cr, z}^{2}} \frac{1}{α_{cr, τ}^{2}}]}^{1 / 2}

Wzór 1

Jak widać, stopnie wykorzystania oraz współczynniki obciążenia krytycznego są określane osobno dla poszczególnych składowych naprężeń lub muszą być znane. Współczynniki obciążenia krytycznego można określić, ponownie obliczając krytyczne naprężenia wyboczeniowe płyty. Określenie tego zostało już opisane w tym artykule technicznym:

KB 001345 │ Analiza wyboczenia płyt usztywnionych z wykorzystaniem PLATE-BUCKLING

Dla poszczególnych składowych naprężenia powstają zatem następujące zależności:

\begin{array}{l} α_{cr, x} = \frac{σ_{cr, p, x}}{σ_{x, Ed}} \\ α_{cr, z} = \frac{σ_{cr, p, z}}{σ_{z, Ed}} \\ α_{cr, τ} = \frac{τ_{cr, p}}{τ_{Ed}} \end{array}

Wzór 2

Metoda ta jest szczególnie odpowiednia dla paneli nieusztywnionych lub usztywnionych wzdłużnie dla wyboczenia, które mają odpowiednie wartości wyboczenia z [2] lub [3].

Obliczenia z wykorzystaniem analizy elementów skończonych

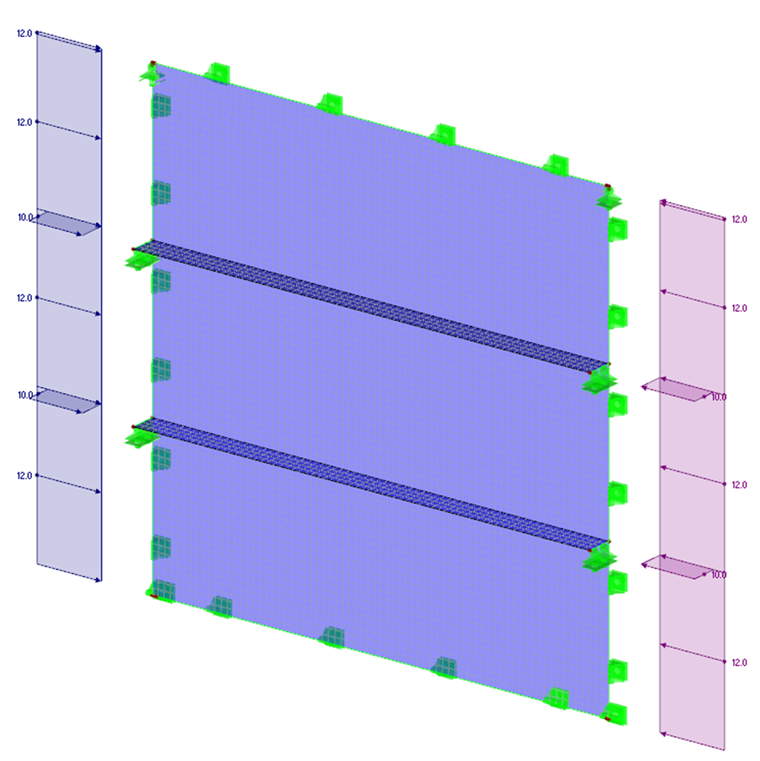
W przypadku silnie usztywnionego panelu z usztywnieniami podłużnymi i poprzecznymi, do określenia obciążenia krytycznego całej konstrukcji należy wykorzystać obliczenia MES. Jako podstawę należy zastosować model powierzchniowy i uwzględnić wszystkie warunki brzegowe (na przykład podpory na krawędziach, położenie geometryczne i obciążenia usztywnienia oraz naprężenia graniczne). W celu wyznaczenia materiału według LBA zastosowano sprężyste zachowanie się materiału. Poniższy przykład ilustruje modelowanie w programie RFEM płyty usztywnionej podłużnie.

FE-Modell eines längsversteiften Beulfeldes

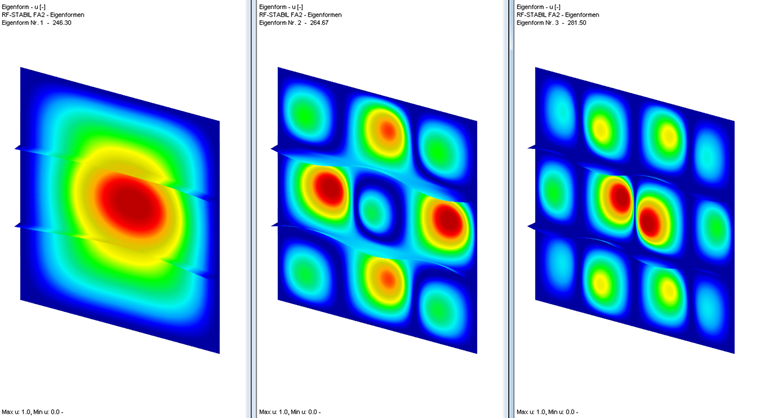
Do określenia współczynnika obciążenia krytycznego służy moduł dodatkowy RF-STABILITY. Przy wyborze postaci własnej należy uwzględnić globalną awarię układu.

Ergebnisse der Eigenformen

Pierwszy Postać własna w tym przykładzie przedstawia wyboczenie globalne, dlatego należy ją traktować jako decydującą. Jednak w niektórych przypadkach kształty wyższych drgań mogą być istotne dla obliczeń. Dzięki temu współczynnik obciążenia krytycznego można obliczyć dla wszystkich składowych naprężenia, a także osobno (tylko jedna składowa naprężenia na przypadek obciążenia).

Samodzielny program PLATE-BUCKLING umożliwia przeprowadzenie pełnej analizy wyboczenia metodą zredukowanych naprężeń wraz z automatycznym określeniem wartości własnych dla każdej składowej naprężenia.

Współczynnik obciążenia krytycznego w analizie wyboczenia

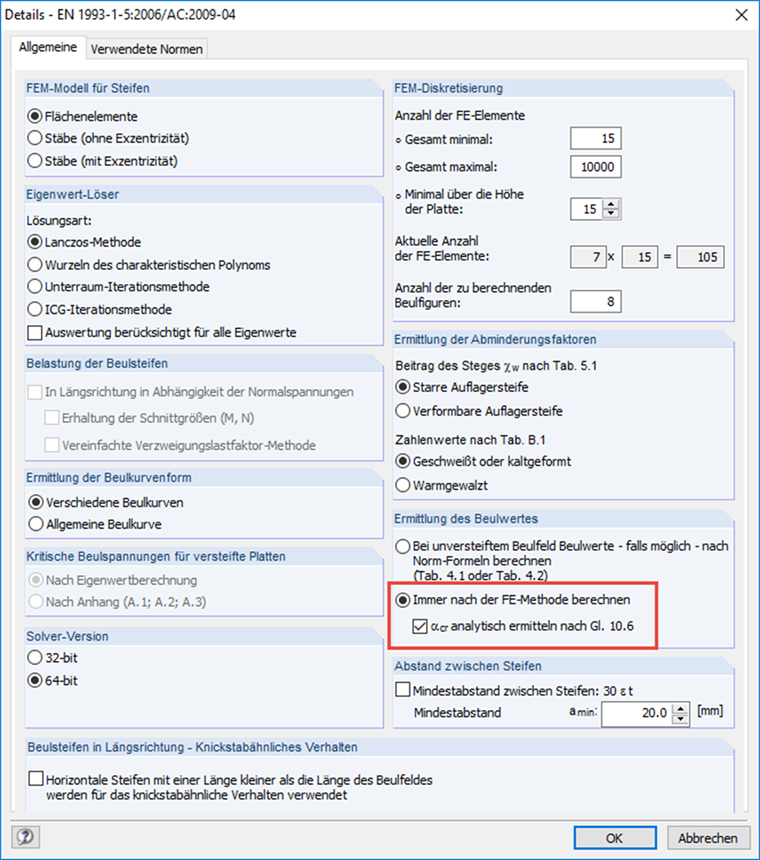
Teraz można określić poszczególne współczynniki obciążenia krytycznego i obliczyć całkowity współczynnik obciążenia krytycznego za pomocą równania. 10.6 w [1] lub wykorzystać je bezpośrednio z obliczeń MES. W niektórych przypadkach rozwiązanie analityczne można uznać za konserwatywne. Dlatego w PLATE-BUCKLING dostępne są następujące opcje.

Kritischen Lastfaktor analytisch berechnen oder aus FEM-Berechnung verwenden

Odnośniki

Oprogramowanie Dlubal Software do analizy stateczności

Odniesienia

Eurokod 3: Projektowanie konstrukcji stalowych - Część 1-5: Platerowane elementy konstrukcyjne. Wydawnictwo Beuth GmbH.
Kurta Klöppela i Joachima Scheera. Wartości wyboczenia usztywnionych płyt prostokątnych, objętości 1. Wilhelm Ernst & Sohn.
Kurda Klöppela i Karla Heinricha Möllera. Wartości wyboczenia usztywnionych płyt prostokątnych, tom 2. Wilhelm Ernst & Sohn, Berlin, 1968.

Pobrane

Plik modelu w RFEM

11,58 MB

;