与应力相关的临界荷载系数
[1] 提供以下公式(第 10 章中的公式 10.6),用于纯解析计算屈曲区段的临界荷载系数:
正如您所看到的,应力比和临界荷载系数对于各个应力部分必须单独确定,或者必须是已知的。 您可以通过重新计算临界板屈曲应力来确定临界荷载系数。 在这篇技术文章中已经介绍了如何确定这一点:
得出各应力分量之间的关系如下:
该方法特别适用于未加劲或纵向加劲扣件,其屈曲值取 [2] 或 [3] 中相应的屈曲值。
使用有限元分析进行计算
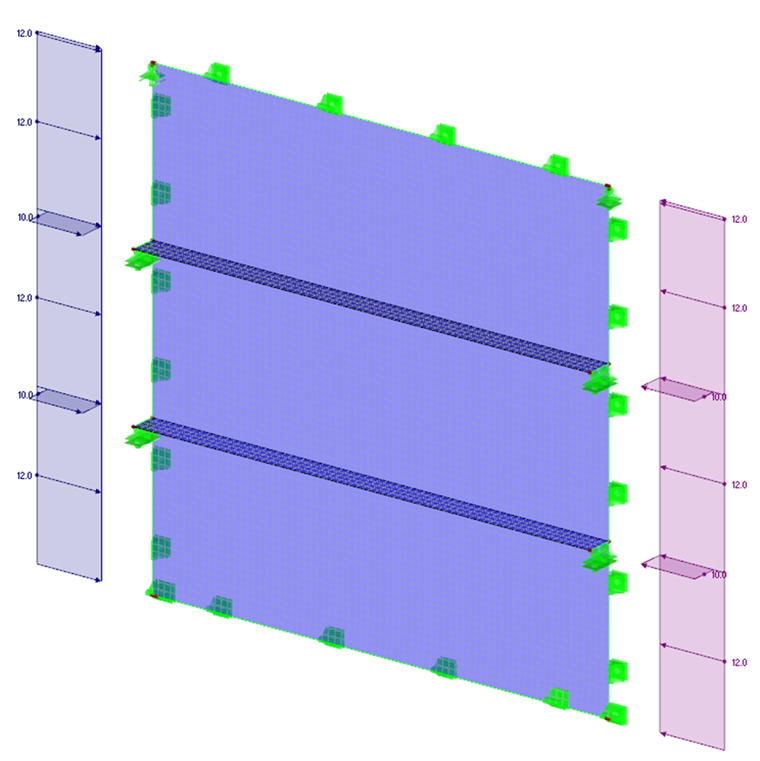
如果是带有纵向和横向加劲肋的屈曲区域,那么作用在整个结构上的临界荷载需要通过有限元方法进行计算。 首先是面模型,并考虑所有边界条件(例如边缘支座、几何位置、加劲肋荷载以及边界应力)。 按照 LBA 方法进行计算时应用弹性材料属性。 下面的示例显示在 RFEM 中对纵向加劲屈曲板建模。
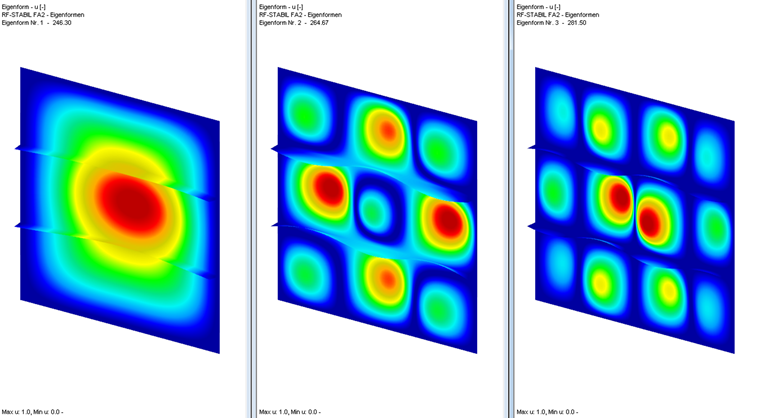
计算临界荷载系数可以在附加模块 RF-STABILITY 中找到。 在选择模态形状时必须考虑全局结构的崩溃。
第一个 本例中的模态显示出整体屈曲,因此应被认为是主导。 在某些情况下,更高的振型可能对设计有意义。 临界荷载系数可以包括所有的应力部分,以及分别计算(每个荷载工况和一个荷载工况只计算一个应力的部分)。
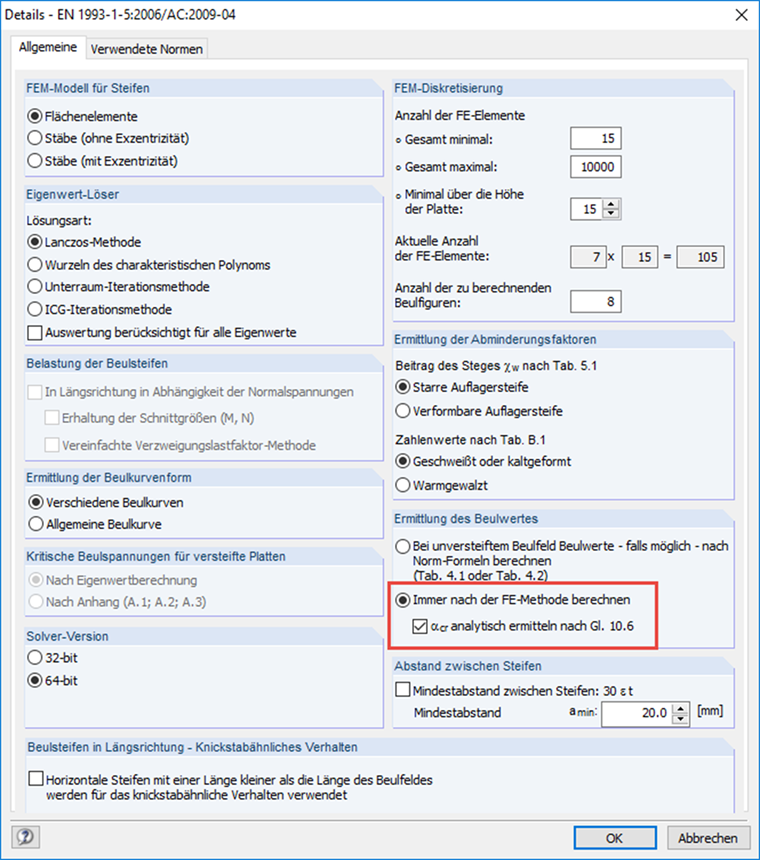
独立程序 PLATE-BUCKLING 可以使用折减应力法进行完整的翘曲分析,包括自动计算每个应力分量的特征值。
屈曲分析中的临界荷载系数
现在可以或者单独确定临界荷载系数,然后利用公式 12 解析计算总的临界荷载系数。 10.6,或者直接使用[1]中的有限元计算。 在某些情况下,解析解可能是保守的。 因此,PLATE-BUCKLING 模块提供以下选项。