Общие сведения
В архитектурном проектировании широко распространена работа с твердотельными моделями. Положение балок и колонн относительно друг друга учитывается посредством расширения сечения. В статическом расчете применяются упрощенные линейные модели, в которых центральные линии пересекаются в общем узле. In RFEM und RSTAB kann der Anwender dieses vereinfachte Modell ebenfalls gerendert darstellen. Часто пересечения отдельных элементов нарушают внешний вид модели и могут вызвать вопросы у заказчика. Для приближения визуализации конструктивной модели к архитектурной модели часто применяются эксцентриситеты стержней. В нашей технической статье для иллюстрации влияния эксцентриситета стержня на определение значений внутренних сил используются три очень простых модели.
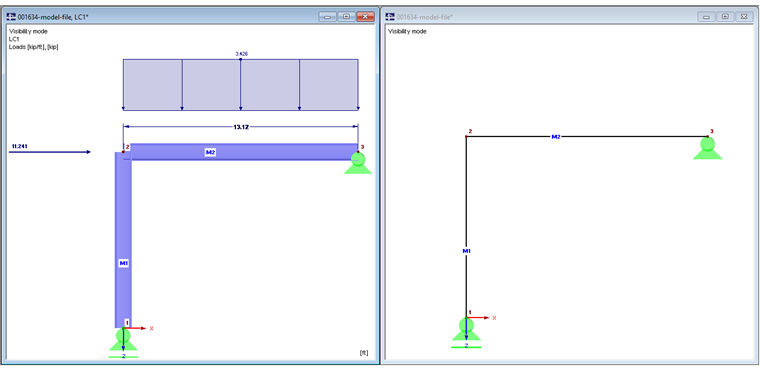
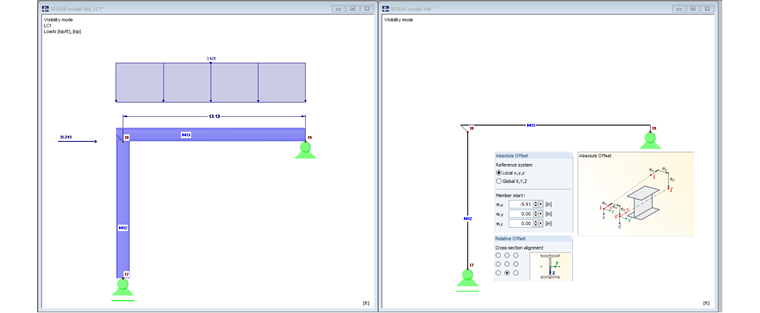
Модель 1 без эксцентриситетов стержней
Träger und Stütze treffen sich in Knoten Nr. 2. Es werden keine Stabexzentrizitäten verwendet.
На рисунке 01 слева показана визуализация модели. Балка доходит только до центральной линии колонны. Колонна также имеет длину до центральной линии балки.
На балку действует распределенная нагрузка, равная 50 кН/м, и нормальная сила, равная 50 кН. Собственный вес стержней для упрощения не учитывается.
Поскольку опорная часть колонны несвязанна в направлении X, то изгибающий момент и поперечная сила балки рассчитываются в данной модели также, как у однопролетной балки.
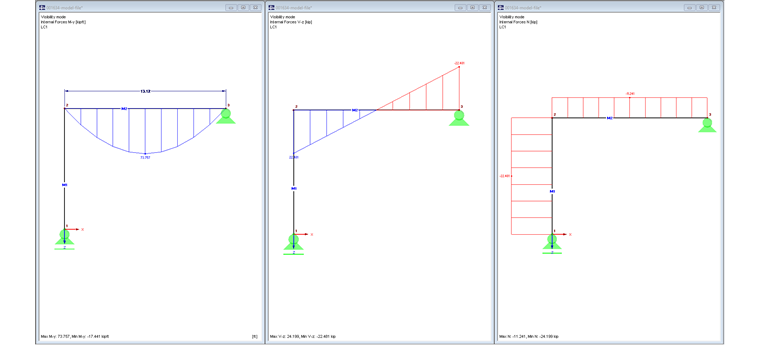
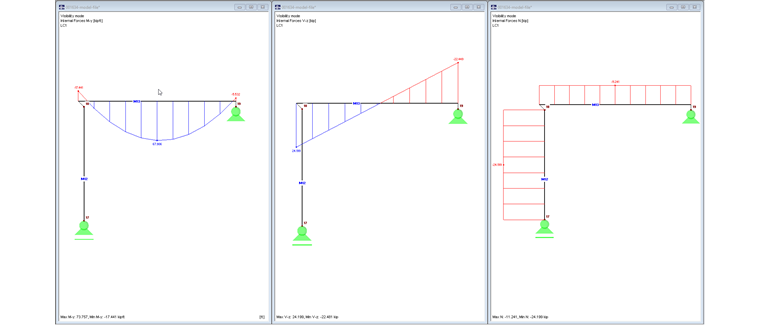
На рисунке 02 показаны внутренние силы My, Vz и N.
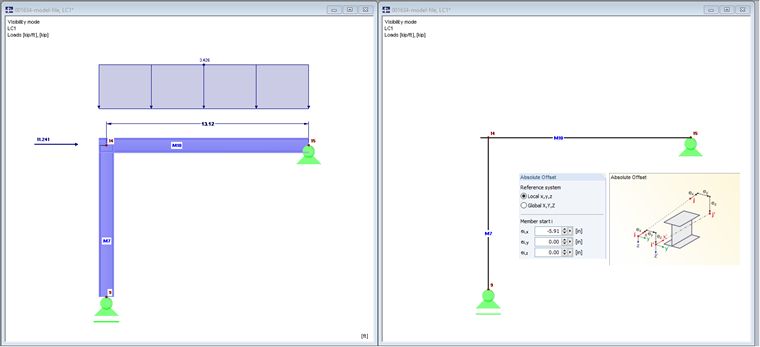
Модель 2 с эксцентриситетом стержня и осевым смещением
Der Stab Nr. 10 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. Такое удлинение поперечной балки увеличивает нагрузку.
На рисунке 03 слева показана визуализация модели.
На балку действует распределенная нагрузка, равная 50 кН/м, и нормальная сила, равная 50 кН. Если принять во внимание собственный вес, их значения также возрастут.
Осевое смещение приводит к удлинению стержня. Das freie Stabende ist dabei starr mit dem Knoten Nr. 14 verbunden.
Поперечное усилие, равное 107,64 кН и приложенное на краю балки, вызывает отрицательный изгибающий момент:
My = 107,64 кН ⋅ -0,15 м = -16,15 кНм
Увеличение вертикальной нагрузки равно 50 кН/м ⋅ 0,15 м = 7,50 кН.
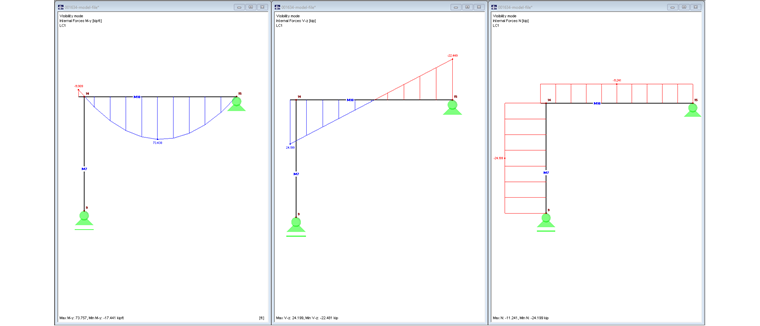
На рисунке 04 показаны внутренние силы My, Vz и N.
Модель 3 с эксцентриситетом стержня, осевым и поперечным смещением
Der Stab Nr. 13 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. Более того, благодаря относительному поперечному смещению данная балка своим нижним краем расположена на верхнем краю колонны.
Визуализация модели показана слева на Рисунке 05.
На балку действует распределенная нагрузка, равная 50 кН/м, и нормальная сила, равная 50 кН. Если принять во внимание собственный вес, их значения также возрастут.
Осевое смещение приводит к удлинению стержня. Das freie Stabende ist dabei starr mit dem Knoten Nr. 18 verbunden.
Поперечное усилие, равное 107,64 кН и приложенное на краю балки, вызывает отрицательный изгибающий момент:
My = 107,64 кН ⋅ -0,15 м = -16,15 кНм
Увеличение вертикальной нагрузки равно 50 кН/м ⋅ 0,15 м = 7,50 кН.
Вертикальное смещение размером 150 мм приводит при действующей нормальной силе размером 50 кН к дополнительному постоянному моменту:
My = 50 кН ⋅ -0,15 м = -7,50 кНм
Однако, вследствие применения эксцентриситета стержня увеличивается отрицательный угловой момент на:
My = -16,15 кНм + (-7,50 кНм) = -23,65 кНм
Внутренние силы My, Vz и N показаны на Рисунке 06.
Заключение
Правильно использованные эксцентриситеты стержней могут привести к более точным результатам расчета конструкций. Однако, на данных простых примерах хорошо видно, что эксцентриситеты могут, кроме прочего, привести к изменениям внутренних сил, причем в случае сложных конструкций может быть трудно проследить, до какой степени изменения связаны с эксцентриситетами.