基本
在建筑领域中经常需要使用实体模型。 Dabei werden die Lage von Trägern und Stützen zueinander über die Ausdehnung des Querschnittes berücksichtigt. In der Statik nutzt man vereinfachte Linienmodelle, bei denen die Mittellinien sich in einem Knoten treffen. In RFEM und RSTAB kann der Anwender dieses vereinfachte Modell ebenfalls gerendert darstellen. Oft stören dann die Verschneidungen der einzelnen Bauteile die Optik und können zu Fragen bei der Bauherrenschaft führen. Oft werden nun Stabexzentrizitäten verwendet, um die Darstellung des Statikmodells an die des Architekturmodells anzunähern. In diesem Fachbeitrag werden drei sehr einfache Modelle verwendet, um den Einfluss der Stabexzentrizität auf die Schnittgrößenermittlung zu verdeutlichen.
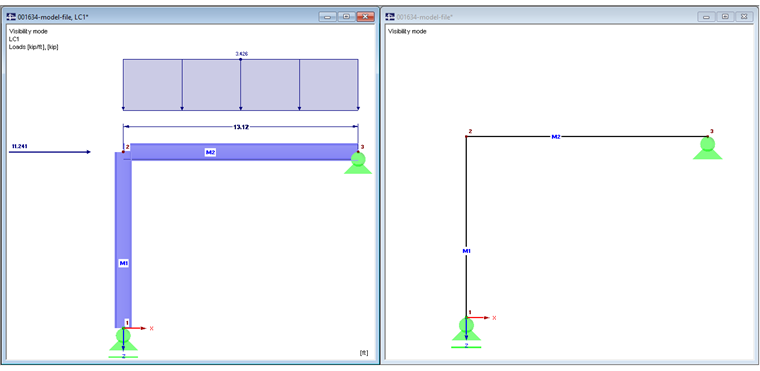
Modell 1 ohne Stabexzentrizitäten
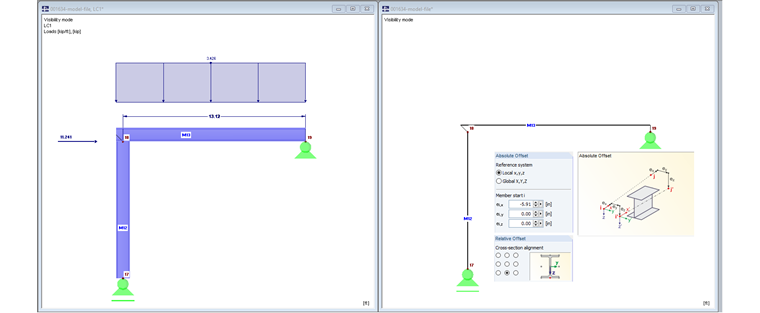
Träger und Stütze treffen sich in Knoten Nr. 2. Es werden keine Stabexzentrizitäten verwendet.
Bild 01 zeigt links das gerenderte Modell. Der Träger geht nur bis zur Mittellinie der Stütze. Die Stütze geht ebenfalls bis zur Mittellinie des Trägers.
Der Riegel ist mit einer Streckenlast von 50 kN/m und einer Normalkraft von 50 kN belastet. Das Eigengewicht der Stäbe wird zur Vereinfachung vernachlässigt.
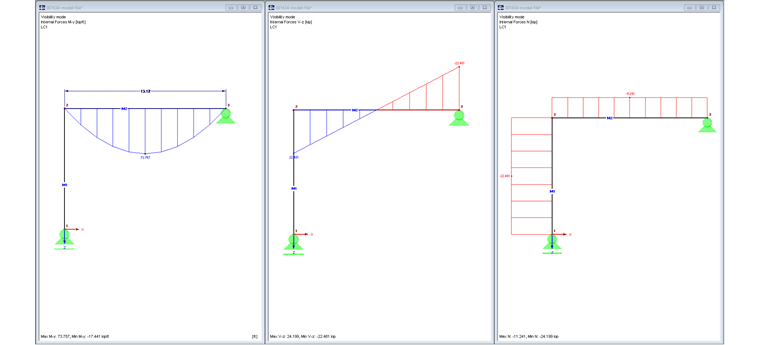
Da das Stützenauflager in X-Richtung frei ist, ergeben sich bei diesem Modell das Biegemoment und die Querkraft des Riegels wie für einen Einfeldträger.
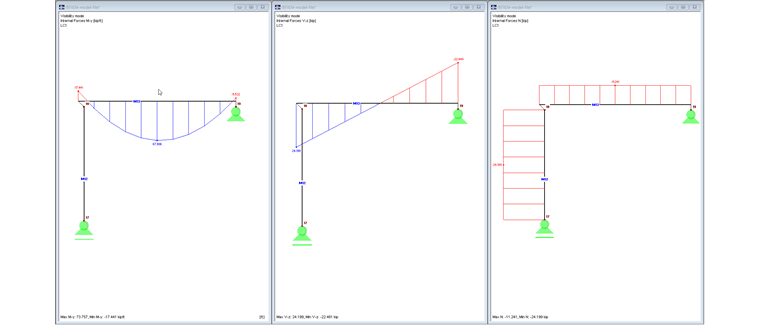
In Bild 02 werden die Schnittgrößen My, Vz und N dargestellt.
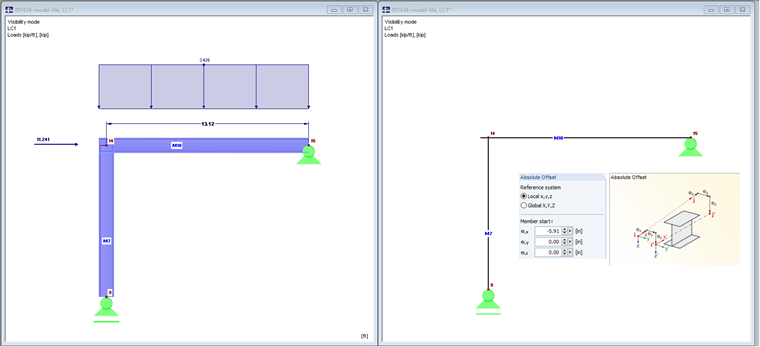
Modell 2 mit Stabexzentrizität, axialer Versatz
Der Stab Nr. 10 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. Durch diese Verlängerung des Riegels erhöht sich ebenfalls die Belastung.
Bild 03 zeigt links das gerenderte Modell.
Der Riegel ist mit einer Streckenlast von 50 kN/m und einer Normalkraft von 50 kN belastet. Würde man das Eigengewicht berücksichtigen, wäre dieses auch erhöht.
Der axiale Versatz führt zu einer Verlängerung des Stabes. Das freie Stabende ist dabei starr mit dem Knoten Nr. 14 verbunden.
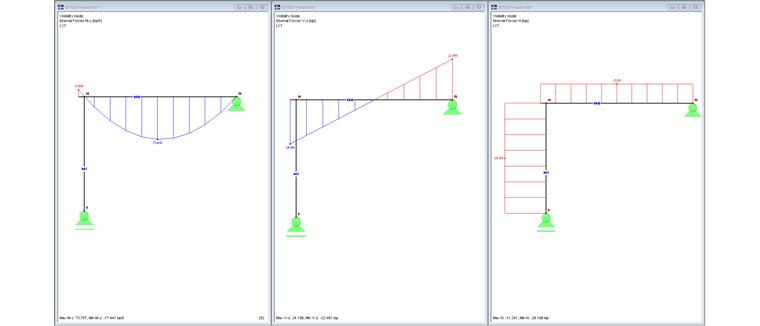
Die einwirkende Querkraft von 107,64 kN am Rand bewirkt ein negatives Biegemoment:
My = 107,64 kN ⋅ -0,15 m = -16,15 kNm
Die Erhöhung der Vertikallast beträgt 50 kN/m ⋅ 0,15 m = 7,50 kN.
In Bild 04 werden die Schnittgrößen My, Vz und N dargestellt.
Modell 3 mit Stabexzentrizität, axialer Versatz und Querversatz
Der Stab Nr. 13 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. Weiterhin wird durch einen relativen Querversatz der Träger mit seiner Unterkante auf der Oberkante der Stütze positioniert.
Bild 05 zeigt links das gerenderte Modell.
Der Riegel ist mit einer Streckenlast von 50 kN/m und einer Normalkraft von 50 kN belastet. Würde man das Eigengewicht berücksichtigen, wäre dieses auch erhöht.
Der axiale Versatz führt zu einer Verlängerung des Stabes. Das freie Stabende ist dabei starr mit dem Knoten Nr. 18 verbunden.
Die einwirkende Querkraft von 107,64 kN am Rand bewirkt ein negatives Biegemoment:
My = 107,64 kN ⋅ -0,15m = -16,15 kNm
Die Erhöhung der Vertikallast beträgt 50 kN/m ⋅ 0,15 m = 7,5 kN.
Der vertikale Querversatz von 150 mm führt durch die einwirkende Normalkraft von 50 kN zu einem zusätzlichen konstanten Moment:
My = 50 kN ⋅ -0,15m = -7,50 kNm
Das negative Eckmoment, allein aus der Verwendung der Stabexzentrizität erhöht sich dadurch:
My = -16,15 kNm + (-7,50 kNm) = -23,65 kNm
In Bild 06 werden die Schnittgrößen My, Vz und N dargestellt.
概述总结
Stabexzentrizitäten können, richtig eingesetzt, zu einem genaueren statischen System führen. Diese einfachen Beispiele verdeutlichen, dass Exzentrizitäten aber auch zu Änderungen in den Schnittgrößen führen und diese bei komplexen Systemen teilweise nur noch schwer auf die Anwendung der Stabexzentrizitäten zurückführbar sein können.