Ogólne informacje
Dla potrzeb architektonicznych powszechne jest stosowanie modeli bryłowych. Wzajemne położenie belek i słupów jest uwzględniane przez wyciągnięcie przekroju bryły. W analizie statycznej stosowane są uproszczone modele analityczne - pręty odwzorowane są przez linie środkowe elementów i stykają się we wspólnym węźle w miejscu ich przecięcia. W programach RFEM i RSTAB ten uproszczony model można wyświetlać również w postaci renderowanej. Przecięcia poszczególnych elementów często zakłócają ogólny wygląd i mogą prowadzić do pytań ze strony klienta. Mimośrody prętowe są często stosowane w celu przybliżenia reprezentacji modelu analitycznego w stosunku do modelu architektonicznego. W artykule tym wykorzystano trzy bardzo proste modele, aby zilustrować wpływ mimośrodu pręta na wyznaczone siły wewnętrzne.
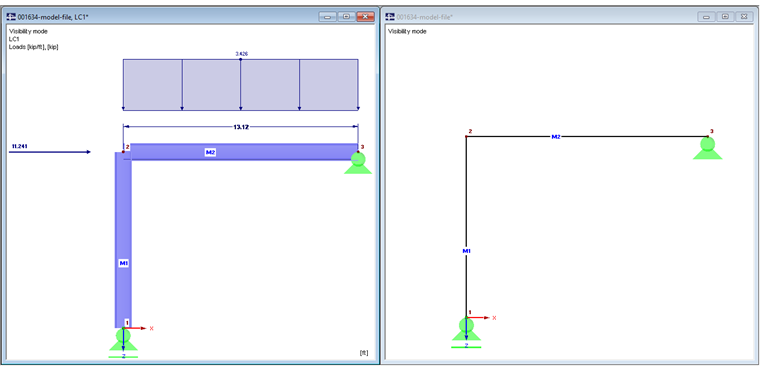
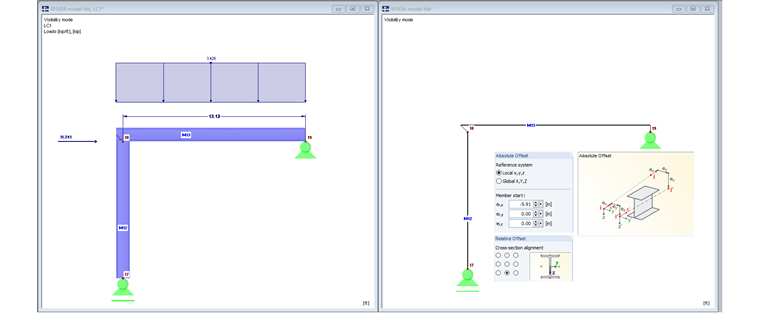
Model 1 bez mimośrodów prętowych
Belka i słup spotykają się w węźle 2. Es werden keine Stabexzentrizitäten verwendet.
Rysunek 01 przedstawia model renderowany po lewej stronie. Belka przebiega tylko do środkowej linii słupa. Słup przebiega również do środkowej linii belki.
Obciążenie belki to siła liniowa 50 kN/m oraz siła osiowa 50 kN. W celu uproszczenia pominięto ciężar własny prętów.
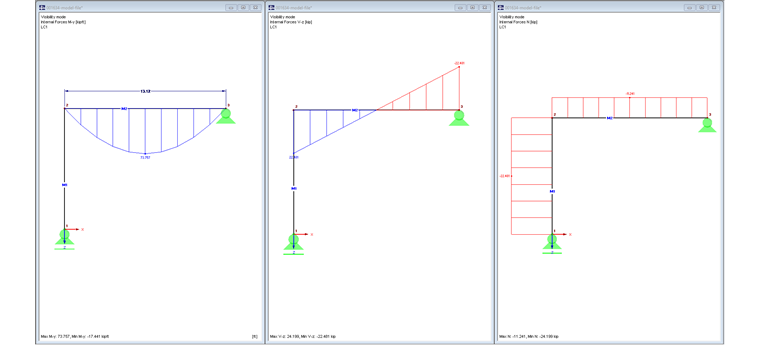
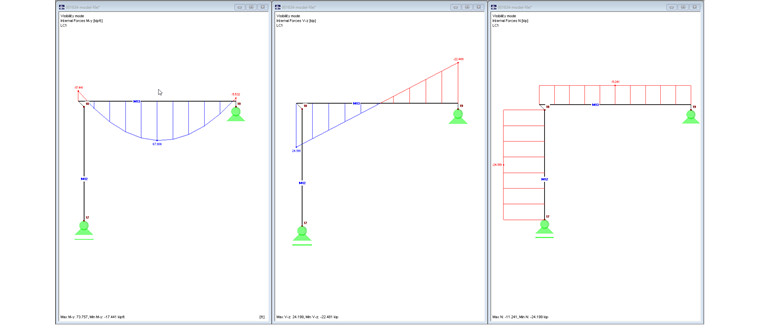
Ponieważ podpora słupa jest ma możliwość przesuwu w kierunku X, moment zginający i siła tnąca belki mają w tym modelu przebieg jak w przypadku belki jednoprzęsłowej.
Rysunek 02 przedstawia siły wewnętrzne My , Vz i N.
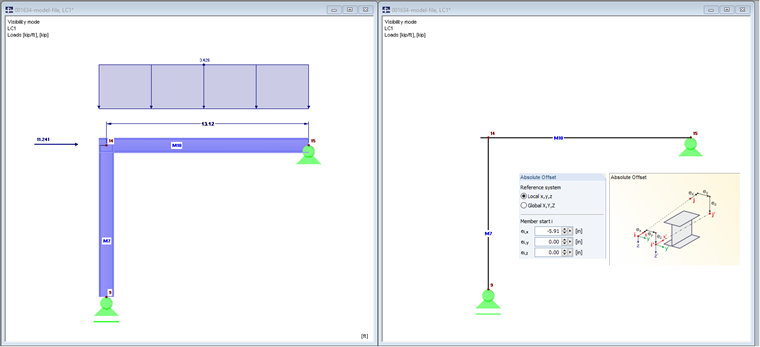
Model 2 z mimośrodem pręta, przesunięcie osiowe
Der Stab Nr. 10 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. To przedłużenie belki zwiększa również obciążenie.
Rysunek 03 przedstawia model renderowany po lewej stronie.
Obciążenie belki to siła liniowa 50 kN/m oraz siła osiowa 50 kN. Jeżeli uwzględniono by ciężar własny, również zostałby on zwiększony.
Przesunięcie osiowe powoduje wydłużenie pręta. Das freie Stabende ist dabei starr mit dem Knoten Nr. 14 verbunden.
Siła tnąca o wartości 107,64 kN działająca na krawędzi powoduje ujemny moment zginający:
My = 107,64 kN ⋅ -0,15 m = -16,15 kNm
Zwiększenie obciążenia pionowego wynosi 50 kN/m ⋅ 0,15 m = 7,50 kN.
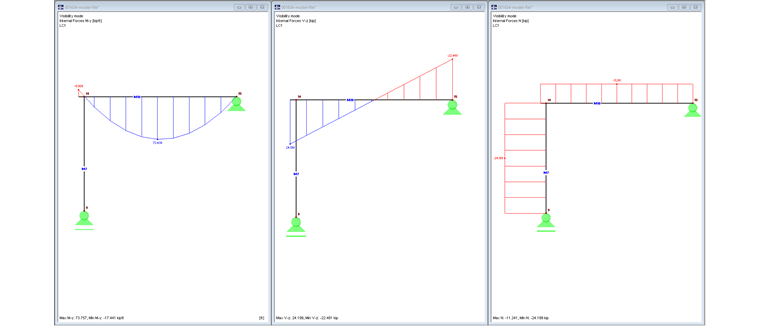
Rysunek 04 przedstawia siły wewnętrzne My , Vz i N.
Model 3 z mimośrodem pręta, przesunięcie osiowe i przesunięcie poprzeczne
Der Stab Nr. 13 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. Ponadto, belka zlicowana jest dolną krawędzią z górną krawędzią słupa o względne przesunięcie poprzeczne.
Rysunek 05 przedstawia model renderowany po lewej stronie.
Obciążenie belki to siła liniowa 50 kN/m oraz siła osiowa 50 kN. Jeżeli uwzględniono by ciężar własny, również zostałby on zwiększony.
Przesunięcie osiowe powoduje wydłużenie pręta. Das freie Stabende ist dabei starr mit dem Knoten Nr. 18 verbunden.
Siła tnąca o wartości 107,64 kN działająca na krawędzi powoduje ujemny moment zginający:
My = 107,64 kN ⋅ -0,15 m = -16,15 kNm
Zwiększenie obciążenia pionowego wynosi 50 kN/m ⋅ 0,15 m = 7,5 kN.
Pionowe przesunięcie poprzeczne wynoszące 150 mm powoduje powstanie dodatkowego momentu stałego, wywołanego działającą siłą osiową 50 kN:
My = 50 kN ⋅ -0,15m = -7,50 kNm
Ujemny moment zginający w narożu spowodowany zastosowaniem mimośrodu pręta zwiększa się o:
My = -16,15 kNm + (-7,50 kNm) = -23,65 kNm
Rysunek 06 pokazuje siły wewnętrzne My , Vz i N.
Uwagi końcowe
Właściwie zastosowane mimośrody pręta pozwalają na stworzenia dokładniejszego odwzorowania układu konstrukcyjnego. Te proste przykłady ilustrują jednak, że mimośrody prowadzą również do różnic w wyliczonych siłach wewnętrznych. Należy więc mieć to na uwadze w przypadku złożonych układów konstrukcyjnych gdzie prześledzenie wpływu mimośrodów prętowych może być czasem utrudnione.