Vliv excentricit prutu na výpočet vnitřních sil

Obecné

V architektonických modelech se běžně pracuje s tělesy. Vzájemnou polohu nosníků a sloupů lze přitom zohlednit rozměrem průřezu. Ve statickém modelu se používají zjednodušené liniové modely, v nichž se středové linie setkávají ve společném uzlu. V programech RFEM a RSTAB lze tento zjednodušený model zobrazit také v renderovacím režimu. Průniky jednotlivých konstrukčních prvků jsou pak rušivým elementem a mohou vyvolávat dotazy zákazníka. Pro přiblížení statického modelu architektonickému modelu se často používají excentricity prutů. V našem příspěvku si na třech velmi jednoduchých modelech ukážeme, jaký vliv má excentricita prutu na stanovení vnitřních sil.

Model 1 bez excentricit prutu

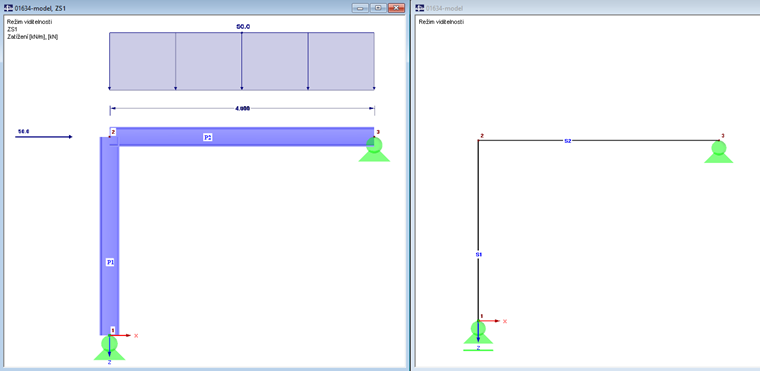
Nosník a sloup se setkávají v uzlu 2. Es werden keine Stabexzentrizitäten verwendet.

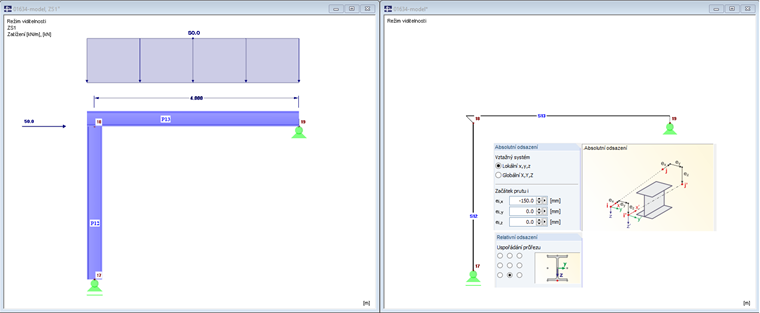
Na obr. 01 vlevo vidíme renderovaný model. Nosník sahá pouze ke střednici sloupu. Také sloup dosahuje ke střednici nosníku.

Na příčel působí spojité zatížení 50 kN/m a normálová síla 50 kN. Vlastní tíhu prutů pro zjednodušení zanedbáme.

1 Model 1 bez excentricit prutu

Protože je podpora sloupu volná ve směru X, jsou v tomto modelu ohybový moment a posouvající síla v příčli stejné jako u nosníku o jednom poli.

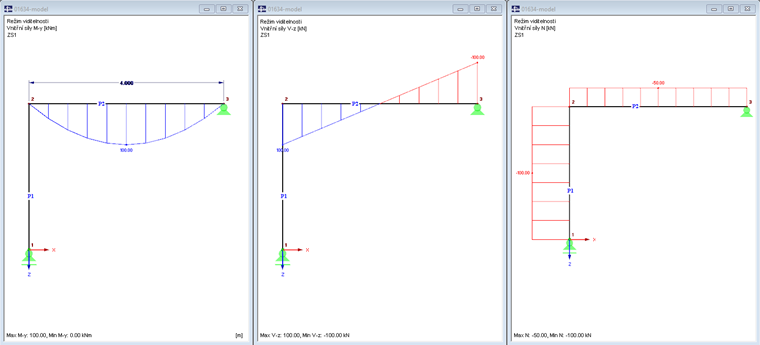
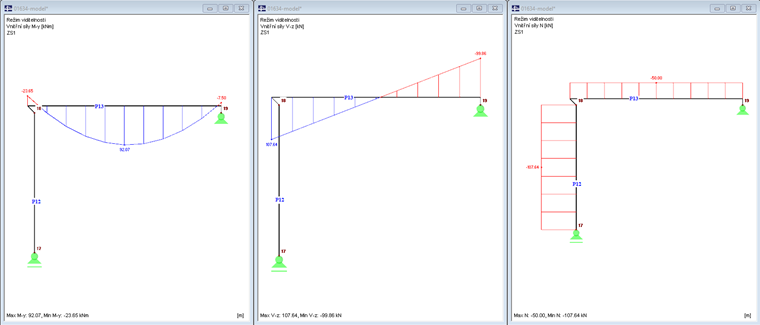
Na obr. 02 jsou znázorněny vnitřní síly M_y, V_z a N.

2 Průběh vnitřních sil u modelu 1

Model 2 s excentricitou prutu a axiálním odsazením

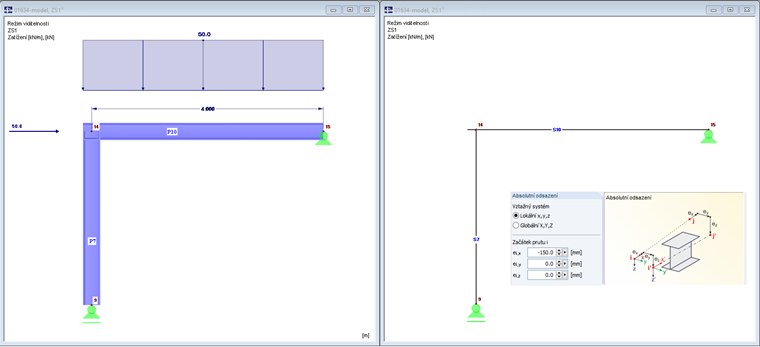
Der Stab Nr. 10 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. V důsledku prodloužení příčle se také zvyšuje zatížení.

Na obr. 03 vlevo je znázorněný renderovaný model.

Na příčel působí spojité zatížení 50 kN/m a normálová síla 50 kN. Pokud bychom uvažovali vlastní tíhu, byla by také vyšší.

3 Model 2 s excentricitou prutu a axiálním odsazením

Axiální odsazení vede k prodloužení prutu. Das freie Stabende ist dabei starr mit dem Knoten Nr. 14 verbunden.

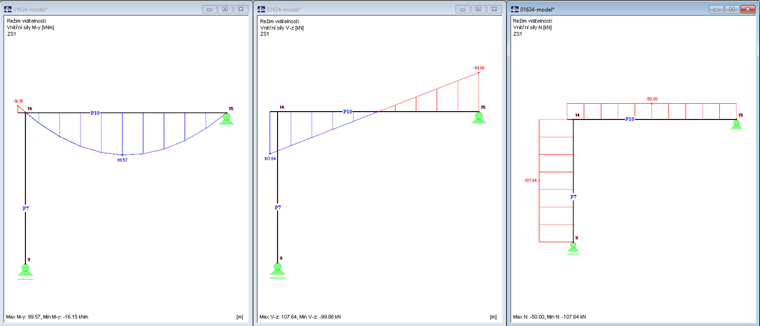
Posouvající síla 107,64 kN na okraji vyvolává záporný ohybový moment:
M_y = 107,64 kN ⋅ -0,15 m = -16,15 kNm

Zvýšení svislého zatížení činí 50 kN/m ⋅ 0,15 m = 7,50 kN.

Na obr. 04 jsou znázorněny vnitřní síly M_y , V_z a N.

4 Průběh vnitřních sil u modelu 2

Model 3 s excentricitou prutu, axiálním a příčným odsazením

Der Stab Nr. 13 wird über einen axialen Versatz von 150 mm bis an die Außenkante der Stütze geführt. Dále pak je poměrným příčným odsazením nosník svou spodní hranou umístěn na horní hranu sloupu.

Na obr. 05 vlevo vidíme renderovaný model.

Na příčel působí spojité zatížení 50 kN/m a normálová síla 50 kN. Pokud bychom uvažovali vlastní tíhu, byla by také vyšší.

5 Model 3 s excentricitou prutu, axiálním a příčným odsazením

Axiální odsazení vede k prodloužení prutu. Das freie Stabende ist dabei starr mit dem Knoten Nr. 18 verbunden.

Posouvající síla 107,64 kN na okraji vyvolává záporný ohybový moment:
M_y = 107,64 kN ⋅ -0,15m = -16,15 kNm

Zvýšení svislého zatížení činí 50 kN/m ⋅ 0,15 m = 7,50 kN.

Svislé příčné odsazení 150 mm vyvolává při působící normálové síle 50 kN přídavný konstantní moment:
M_y = 50 kN ⋅ -0,15m = -7,50 kNm

Záporný moment v rohu se tak čistě vlivem excentricity prutu zvyšuje:
M_y = -16,15 kNm + (-7,50 kNm) = -23,65 kNm

Na obr. 06 jsou znázorněny vnitřní síly M_y , V_z a N.

6 Průběh vnitřních sil u modelu 3

Závěr a výhled

Pokud se správně zohlední excentricity prutů, dosáhneme přesnějšího statického systému. Na těchto jednoduchých příkladech vidíme, že excentricity mohou ovšem také vést ke změnám vnitřních sil, a u složitých konstrukcí může být někdy obtížné vysledovat, do jaké míry je lze vztáhnout na excentricity prutů.