Dimensionamento de viga de madeira segundo a norma 2018 NDS

Análise de vigas de madeira

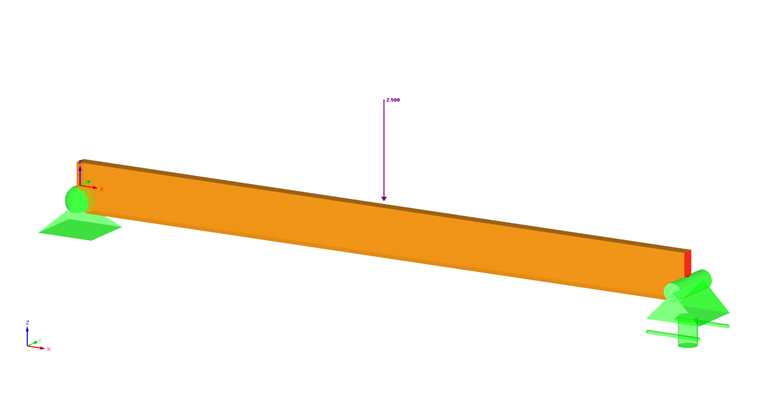
Será dimensionada uma viga estrutural selecionada de abeto de Douglas-Larch (norte) com 4,6 m ⋅ 14 polegadas de comprimento, com uma carga pontual a meio do vão de 2,500 kip. O objetivo desta análise é determinar os fatores de flexão ajustados e a capacidade de flexão da viga. É assumida uma duração de carga normal e suportes fixos em cada extremidade da barra. Os critérios de carregamento são simplificados para este exemplo. O critério de carregamento normal pode ser referenciado na secção 1.4.4 [1]. Na Figura 01, é apresentado um diagrama da viga simples com cargas e dimensões.

1 Carga da viga e detalhes dimensionais

Propriedades da viga

A secção utilizada neste exemplo é uma madeira de dimensão nominal de 4 polegadas ⋅ 14 polegadas. Os cálculos reais das propriedades da secção da viga de madeira podem ser consultados abaixo:

• b = 3,50 polegadas
• d = 13,25 polegadas
• L = 15 pés

• Área de secção bruta:
  $${\mathrm{A}}_{\mathrm{g}}= \mathrm{b} · \mathrm{d} = (3.50 \mathrm{in}) · (13.25 \mathrm{in}) = 46.38 {\mathrm{in}}^2$$

  área de secção bruta
• Módulo da secção:
  $${\mathrm{S}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^2}{6} = \frac{(3.50 \mathrm{in}) · {(13.25 \mathrm{in})}^2}{6} = 102.41 {\mathrm{in}}^3$$

  Módulo de rigidez
• Momento de inércia:
  $${\mathrm{I}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^3}{12} = \frac{(3.50 \mathrm{in}) · {(13.25 \mathrm{in})}^3}{12} = 678.48 {\mathrm{in}}^4$$

  momento de inércia

O material que será utilizado para este exemplo é "Select Structural Douglas Fir-Larch (North)". As propriedades do material são as seguintes:

• Valor de cálculo da flexão de referência: F_b = 1350 psi
• Módulo de elasticidade mínimo: E_mín = 690 000 psi

Fatores de ajuste da viga

Para o dimensionamento de barras de madeira de acordo com a norma NDS 2018 e o método ASD, têm de ser aplicados fatores de estabilidade (ou fatores de ajuste) ao valor de cálculo de flexão de referência (F_b). Isto irá providenciar o valor de cálculo da flexão ajustado (F'_b). O fator F'_b é determinado de acordo com a seguinte equação, dependendo em grande medida dos fatores de ajustamento apresentados na tabela 4.3.1 [1]:

Abaixo, é determinado cada fator de ajuste:

C_D

O fator de duração da carga é implementado para ter em consideração diferentes períodos de carregamento. A neve, o vento e os sismos são tidos em consideração com C_D. Este fator tem de ser multiplicado por todos os valores de dimensionamento de referência exceto o módulo de elasticidade (E), o módulo de elasticidade para a estabilidade de vigas e pilares (E_min) e as forças de compressão perpendiculares às fibras (F_c) baseadas na secção 4.3.2 [1]. C_D neste caso é definido como 1,00 de acordo com a secção 2.3.2 [1], assumindo uma duração normal de carga de 10 anos.

C_M

O fator de utilização em piso molhado refere os valores de dimensionamento para madeira estrutural serrada com base nas condições de utilização em humidade especificadas na secção 4.1.4 [1]. Neste caso, com base na secção 4.3.3 [1], C_M está definido como 1,00.

C_t

O fator de temperatura é controlado através da exposição prolongada de uma barra a temperaturas elevadas até 65,5 graus Celsius. Todos os valores de cálculo de referência serão multiplicados por C_t. Utilizando a tabela 2.3.3 [1], C_t é definido como 1,00 para todos os valores de dimensionamento de referência, assumindo que as temperaturas são inferiores ou iguais a 100 graus Fahrenheit.

C_F

O fator de tamanho para madeira serrada tem em consideração o facto de a madeira não ser um material homogéneo. O tamanho da viga e o tipo de madeira são tidos em consideração. Para este exemplo, a nossa viga tem uma largura entre 5 cm e 10 cm e uma altura nominal de 22 cm. Referenciando a tabela 4A com base no material e tamanho da viga, é aplicado um coeficiente de 1,00. Esta informação pode ser encontrada na secção 4.3.6.1 [1].

C_i

O fator de incisão é utilizado para ter em conta o tratamento de preservação que a madeira recebe para resistir à decomposição que pode causar o crescimento de fungos. Na maioria das vezes, isso envolve um tratamento por pressão, mas em alguns casos é necessário fazer uma incisão na madeira, aumentando a área de superfície para o recobrimento químico. Para este exemplo, assumimos que a madeira é incisada. Referindo a tabela 4.3.8 [1], é apresentada uma vista geral sobre quais os fatores que cada uma das propriedades da barra tem de ser multiplicada.

_r

O fator de barra repetitiva é utilizado nos casos em que várias barras de madeira serrada atuam de forma uniforme, levando a uma distribuição uniforme da carga entre as barras. Estas barras não podem ter um espaçamento superior a 24 polegadas do centro. Neste exemplo, assumiremos que a viga se encontra com um espaçamento reduzido e conectada por qualquer cobertura ou plataforma. Neste caso, o fator de barra repetitiva C_r é igual a 1,15 da secção 4.3.9 [1].

C_L

O fator de estabilidade da viga verifica que a encurvadura por torção ou deformação do eixo fraco não ocorre sobre os vãos mais longos sem apoio lateral. Isto é em referência à secção 5.3.4 [1] e será calculado abaixo.

C_fu

O fator de utilização plano é utilizado quando a carga de uma barra em madeira é aplicada ao eixo fraco versus ao eixo forte. Para este exemplo, irá-se aplicar o carregamento ao eixo forte, por isso, esse fator não será incluído nos nossos cálculos.

C_T

O fator de resistência à encurvadura é utilizado para ter em conta a madeira prensada que pode aumentar a resistência à encurvadura das vigas em compressão das treliça. Para este exemplo, assumiremos que não existe revestimento de madeira contraplacada, pelo que C_T é igual a 1,00.

Módulo de elasticidade ajustado

Os valores do módulo de elasticidade de referência (E e E_min ) também tem de ser ajustados. Os módulos de elasticidade ajustados (E' e E'_min ) são determinados a partir da tabela 4.3.1 [1] e o fator de incisão C_i é igual a 0.95 da tabela 4.3 .8 [1].

Fator de estabilidade da viga (C_L )

O fator de estabilidade da viga (C_L ) é necessário para calcular o valor de cálculo da flexão ajustada da viga e posteriormente para calcular a relação da flexão de cálculo. Os seguintes passos incluirão as equações e os valores necessários para determinar C_L.

O comprimento efetivo desta viga pode ser calculado através do comprimento lateral não apoiado (l_u ), que é o comprimento total da viga. O comprimento da barra convertido em polegadas é utilizado na equação de comprimento efetivo na tabela 3.3.3 [1].

Em seguida, vamos calcular a relação de esbelteza de barras fletidas (R_B) utilizando a secção. 3.3.3.6 [1] com a largura, profundidade e o comprimento do vão efetivo da viga.

Agora, o valor de cálculo da encurvadura crítico para as barras fletidas (F_be) é calculado com referência à secção. 3.3.3.8 [1]. O módulo de elasticidade para a estabilidade da viga (E'_min) é utilizado juntamente com a relação de esbelteza da flexão (R_B ) anteriormente calculada.

O fator de estabilidade da viga (C_L) pode agora ser calculado com referência à mesma secção acima.

O fator de incisão C_i é igual a 0,80 para F_b da tabela 4.3.8 [1]. Agora, todos os fatores de ajuste foram determinados a partir da tabela 4.3.1 [1]. Portanto, o valor de cálculo da flexão ajustado (F'_b) pode ser calculado.

Relação de cálculo da viga

O objetivo final deste exemplo é obter a relação de cálculo para esta viga simples. Isto determinará se o tamanho da viga é adequado para a carga dada ou se deve ser otimizado ainda mais. O cálculo da relação de cálculo requer o momento de flexão máximo e a tensão de flexão real.

O momento máximo sobre o eixo x (M_máx ) é encontrado através da seguinte forma.

De seguida, a tensão de flexão real (f_b) é calculada ligando M_máx e S dos cálculos anteriores. Isto pode ser visto abaixo, utilizando a secção 3.3.2.1 [1].

Por fim, a relação de cálculo (η) de acordo com a secção 3.3.1 pode agora ser calculada.

Aplicação no RFEM

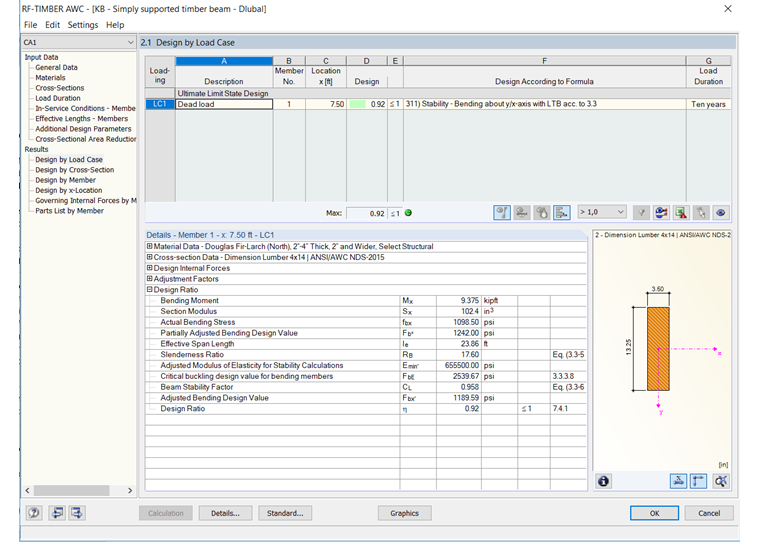
Para o dimensionamento de madeira de acordo com a norma NDS 2018 no RFEM, o módulo adicional RF-TIMBER AWC analisa e otimiza secções com base nos critérios de carga e na capacidade para uma única barra ou um conjunto de barras. Isto encontra-se disponível para os métodos de dimensionamento LRFD ou ASD. Ao modelar e dimensionar o exemplo de viga acima no RF-TIMBER AWC, os resultados podem ser comparados.

• Visualizador 3D
• Visualizador 3D | Babylon
• Realidade virtual

2 Modelo RFEM

Na tabela dos Dados gerais do módulo adicional RF-TIMBER AWC são selecionadas a barra, as condições de carregamento e os métodos de dimensionamento. O material e as secções são definidas a partir do RFEM e a duração da carga é definida para dez anos. A condição de utilização de humidade está definida como Seco e a temperatura é igual ou inferior a 100 graus Fahrenheit. A encurvadura por flexão-torção é definida de acordo com a tabela 3.3.3 [1]. Os cálculos do módulo produzem uma tensão de flexão real (f_b) de 1098,50 psi e um valor de cálculo de flexão ajustado (f'_b) de 1189,59 psi. Uma relação de cálculo (η) de 0,92 é determinada a partir destes valores, alinhando-se bem com os cálculos analíticos manuais apresentados acima.

3 módulo adicional RF-TIMBER AWC