Пункт 8.4.1 [1] перечисляет требования по устойчивости, которые конструктивное проектирование должно учитывать, используя любой из методов. Эти требования включают деформации, влияющие на структуру, эффекты второго порядка, включая P-Δ и P-δ, глобальные и элементные геометрические несовершенства, уменьшение жесткости с учетом текучести элементов и остаточных напряжений, и, наконец, неопределенность в жесткости и прочности структуры.
Пункт 8.4.3 – Упрощенный метод анализа устойчивости
При использовании упрощенного метода анализа устойчивости, указанного в 8.4.3 [1], приведено всего несколько требований.
Геометрическая нелинейность
Первым требованием являются эффекты второго порядка на элементы, или P-Δ, которые можно непосредственно учесть в анализе. Метод расчета анализа второго порядка наиболее распространен во многих современных программах структурного анализа. Альтернативой является усиление всех осевых нагрузок на элементы и изгибающих моментов, полученных из анализа первого порядка, коэффициентом U2, определенным в 8.4.3.2(b) [1]. Этот подход может быть предпочтительным для ручных расчетов или если программа структурного анализа не включает эффекты P-Δ автоматически.
Геометрические несовершенства
Условные горизонтальные нагрузки — это второй элемент, указанный в упрощенном методе в пункте 8.4.3.3 [1]. Эта приложенная нагрузка равна 0,005 от общей фактической гравитационной нагрузки на рассматриваемом уровне и должна быть распределена аналогично гравитационной нагрузке. Условные нагрузки всегда прикладываются в направлении, создающем наибольший дестабилизирующий эффект. Это означает, что такие нагрузки должны быть приложены в том же направлении, что и боковая ветровая нагрузка, чтобы создать наибольшие деформации и внутренние силы в конструкции.
Приложение O.2 – Эффекты устойчивости в упругом анализе
Как альтернатива упрощенному подходу анализа устойчивости, инженеры могут использовать Приложение O.2 для выполнения требований по устойчивости, изложенных в пункте 8.4.1 [1]. Этот подход был добавлен в стандарт 2019 года и имеет много общего с Методом прямого анализа US steel design manual AISC 360-16 Ch. C.
Геометрическая нелинейность
Геометрические нелинейности, или эффекты второго порядка, рассматриваются в O.2.2 [1]. Как и в упрощенном методе, анализ второго порядка можно провести напрямую, включая эффекты нагрузок, действующих в смещенных точках пересечения элементов (эффекты P-Δ). Кроме того, должны быть учтены эффекты осевых нагрузок, действующих на деформированную форму элемента по его длине (P-δ). В O.2.2 [1] даны положения, когда P-δ можно полностью пренебречь. С другой стороны, если P-δ включены напрямую в анализ, коэффициент U1 может быть установлен на уровне 1.0, используемом в пункте 13.8 - Проектирование элементов на осевое сжатие и изгиб [1].
Геометрические несовершенства
Геометрические несовершенства элементов, такие как неоднородность или локальные геометрические несовершенства типа кривизны элементов, не нужно учитывать при проектировании в соответствии с пунктом O.2 [1]. Однако глобальные геометрические несовершенства должны быть учтены с использованием прямого моделирования или условных горизонтальных нагрузок. Есть исключение, когда эти глобальные геометрические несовершенства могут быть пренебрежены для боковых сочетаний нагрузок только при выполнении требований, изложенных в пункте O.2.3.1 [1]. Требования включают то, что гравитационные нагрузки структуры поддерживаются в первую очередь вертикальными структурными элементами, и соотношение между максимальным прогибом второго порядка и прогибом первого порядка с использованием уменьшенной жесткости элемента в соответствии с пунктом O.2.4 [1] не превышает 1,7 на любом уровне этажа.
Если инженер не может пренебречь этими несовершенствами, может быть использован первый метод прямого моделирования. Точки пересечения элементов должны быть смещены по сравнению с их первоначальными местоположениями. Амплитуда этого начального смещения указана в пункте 29.3 [1] и приложена в направлении наибольшего дестабилизирующего эффекта, который для большинства строительных структур составляет отклонение 1/500 для косо стоящих колонн. Значительная проблема этого метода заключается в большом количестве сценариев моделирования, которые необходимо учитывать. Теоретически требуется четыре смещения в четырех разных направлениях на каждом уровне этажа. Если также учесть эффекты кривизны элементов вместе с косостью колонн, это добавляет много дополнительных сценариев моделирования для учета наибольшего дестабилизирующего эффекта.
Альтернативный и предпочтительный метод для глобальных геометрических несовершенств — это применение условных горизонтальных нагрузок. Этот метод разрешен только в том случае, если гравитационные нагрузки в основном поддерживаются вертикальными структурными элементами. Условные горизонтальные нагрузки рассматривались ранее в этой статье и применяются аналогично упрощенному анализу устойчивости в пункте 8.4.3.2 [1]. Однако амплитуда уменьшена с 0.005 до 0.002 от фактической гравитационной нагрузки на соответствующем уровне. Снижение величины разрешено в пункте O.2.3.3, так как эти условные нагрузки учитывают только глобальные геометрические несовершенства, тогда как условные нагрузки в пункте 8.4.3.2 [1] также учитывают эффекты неупругости и другие неопределенности.
Эффекты неупругости
Чтобы учесть эффекты неупругости и также учесть начальные несовершенства элементов или локальные геометрические несовершенства, а также неопределенность в жесткости и прочности, уменьшенная осевая и изгибная жесткость элементов в соответствии с следующими уравнениями в пункте O.2.4 [1] должна быть применена к элементам, вносящим вклад в боковую устойчивость.
(E A)r = 0.8 τb E A (E I)r = 0.8 τb E I Где, Cf / Cy < 0.5 ; τb = 1.0 Cf / Cy > 0.5 ; τb = 4 Cf / Cy (1 - Cf / Cy)
Чтобы избежать локальных искажений, стандарт предлагает применить это снижение жесткости ко всем элементам. Более того, если жесткость на сдвиг (GA) и кручение (GJ) значительно влияют на боковую устойчивость, следует учитывать снижение жесткости. Снижение жесткости не должно использоваться при анализе прогибов, деформаций, вибраций или собственных вибраций.
Применение приложения O.2 в RFEM
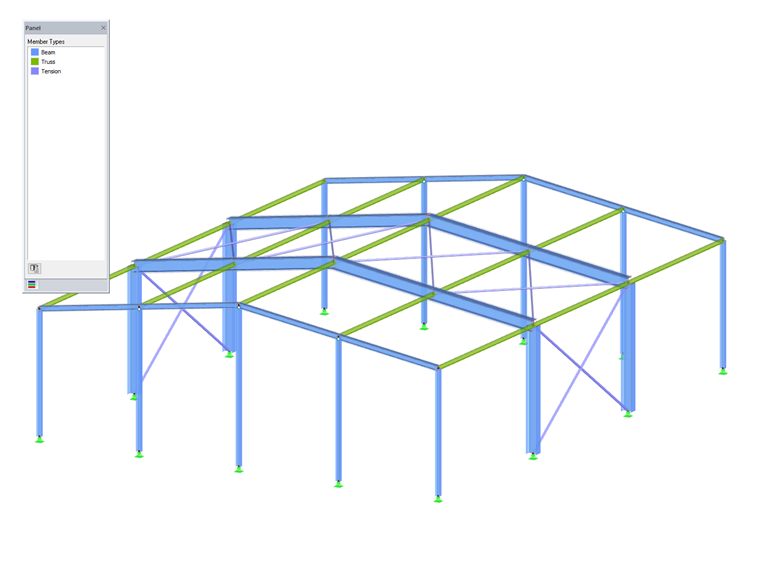
Программа FEA RFEM включила последние требования устойчивости стандарта CSA S16:19 в соответствии с новыми положениями Приложения O.2.
Геометрическая нелинейность
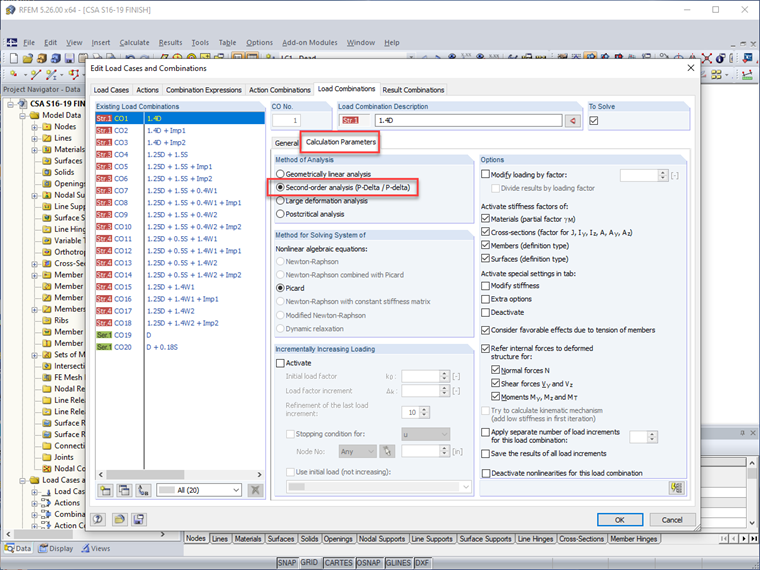
Эффекты второго порядка, установленные в пункте O.2.2 [1], учитываются напрямую для каждого случая или комбинации нагрузки, когда метод расчета настроен на "анализ второго порядка".
Не только эффекты P-Delta включены в анализ элементов, но также учитываются и P-δ. Поэтому коэффициент U1 может быть установлен на 1.0, как указано в пункте 13.8 непосредственно в модуле проектирования элементов RF-/STEEL CSA.
Геометрические несовершенства
Пользователь RFEM имеет возможность напрямую моделировать глобальные геометрические несовершенства путем смещения точек или узлов пересечения элементов. Однако, чтобы этот метод создавал наибольший дестабилизирующий эффект, потребуется проведение множества моделей с различными сценариями. Это достаточно трудоемко и громоздко.
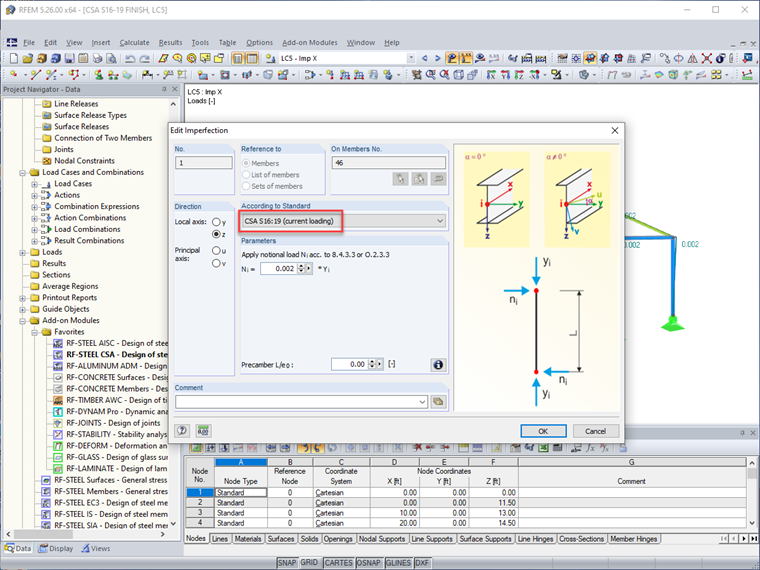
Альтернативный подход заключается в применении условных нагрузок с импершвенным параметрами в RFEM. Этот диалог теперь включает CSA S16:19 в выпадающем списке параметров. Условная нагрузка применяется к концу элемента (т.е. верх колонны) с величиной, равной 0.002 (или 0.005, если используется упрощенный метод устойчивости), умноженной на осевую силу элемента (приложенная гравитационная нагрузка элемента). Равная и противоположная сила применяется внутренне на противоположный конец элемента, чтобы избежать нереалистичных базовых сдвигов структуры.
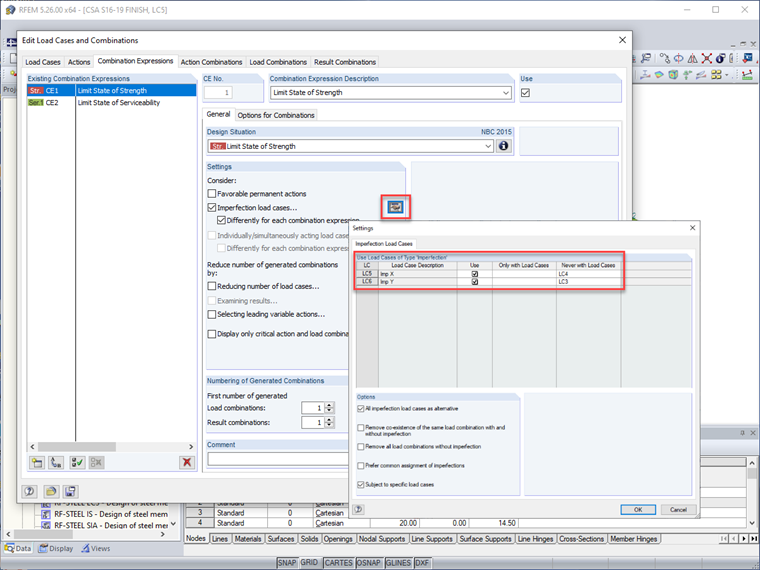
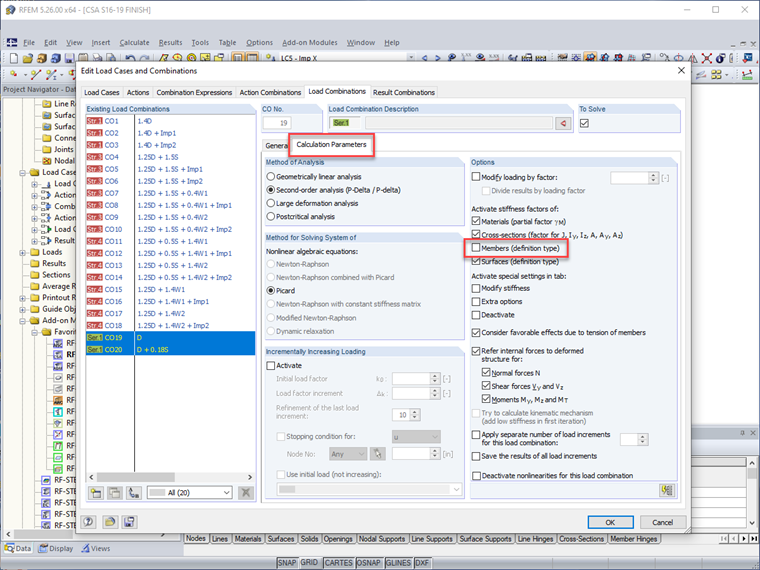
Эти случаи нагрузок несовершенства могут быть применены в RFEM с конкретными случаями боковых нагрузок для обеспечения наибольшего дестабилизирующего действия, избегая при этом генерации сочетаний нагрузок, которые не будут управляющими и увеличат время расчета (т.е. условные нагрузки в направлении X должны применяться только с ветровыми нагрузками в направлении X). Кроме того, несовершенства можно полностью отключить для выражений комбинации нагрузок, таких как эксплуатационная пригодность, при этом они остаются активными для прочностных комбинаций.
Эффекты неупругости
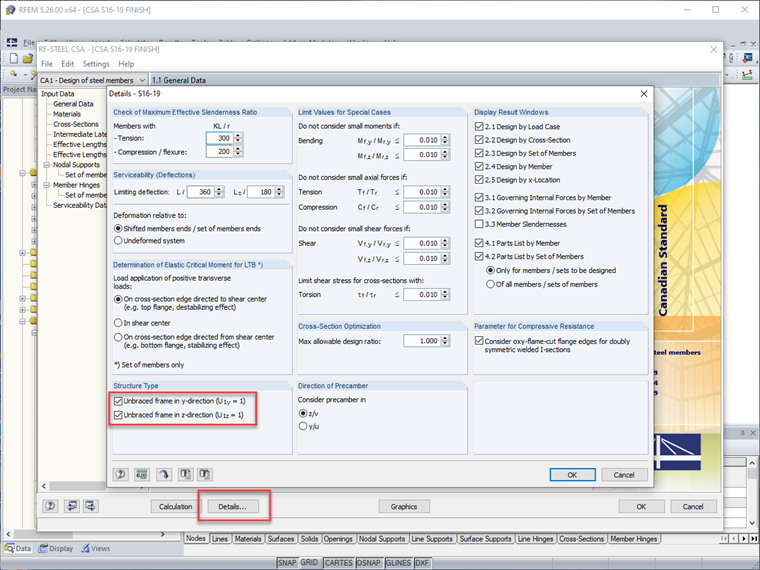
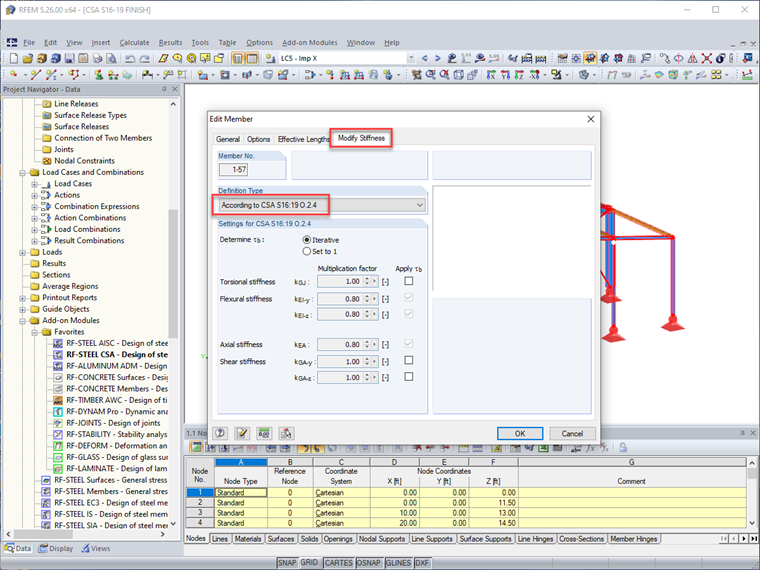
Вкладка изменения жесткости для элементов теперь включает стандарт CSA S16:19. Когда этот параметр выбран, модификационный коэффициент 0.8 и вычисленный τb фактор применяется непосредственно к изгибной и осевой жесткости элемента. Пользователи также имеют возможность дополнительно применить эти сокращения к крутильной и сдвиговой жесткости элемента.
Поскольку снижение жесткости элементов не должно учитываться при проектировании на эксплуатационную пригодность (т.е. прогибы), RFEM позволяет пользователям отключить все модификации жесткости элементов для сочетаний нагрузок на эксплуатационную пригодность, оставляя это активным для сочетаний нагрузок на прочность.
Резюме
Значительные обновления проектирования устойчивости в соответствии с Приложением O.2 в последнем канадском руководстве по проектированию стальных конструкций CSA S16:19 теперь полностью включены в рабочий процесс анализа RFEM. Эти обновления в значительной степени включают возможность учитывать условные нагрузки как несовершенства, а также уменьшенную жесткость элементов в соответствии с CSA S16:19. Для просмотра этих новых обновлений, показанных в детальном видео-примере, ознакомьтесь с вебинаром CSA S16:19 Steel Design в RFEM.