Clause 8.4.1 [1] lists the stability requirements which the structural design should address using either method. These include deformations contributing to the structure, second-order effects including P-Δ and P-δ, global and member geometric imperfections, stiffness reduction accounting for member yielding and residual stresses, and lastly, uncertainty in the structure's stiffness and strength.
Clause 8.4.3 – Simplified Stability Analysis Method
With the simplified stability analysis method given in 8.4.3 [1], only a couple of requirements are listed.
Geometric Nonlinearities
The first includes member second-order effects, or P-Δ, which can be directly considered in the analysis. A second-order analysis calculation method is most common with many structural analysis software programs today. The alternative is to amplify all member axial loads and bending moments obtained from a first-order analysis by the factor U2 defined in 8.4.3.2(b) [1]. This approach may be better suited for hand calculations, or if the structural analysis software does not include P-Δ effects automatically.
Geometric Imperfections
Notional lateral loads are the second item listed under the simplified method in Clause 8.4.3.3 [1]. This applied load is equal to 0.005 times the total factored gravity load at the considered story and should be distributed similarly to the gravity load. Notional loads are always applied in the direction which generates the greatest destabilizing effect. This means such loads should be applied in the same direction as a lateral wind load to generate the highest deformations and internal forces on the structure.
Annex O.2 – Stability Effects in Elastic Analysis
As an alternative to the simplified stability analysis approach above, engineers can utilize Annex O.2 to satisfy the stability requirements set forth in Clause 8.4.1 [1]. This approach was added to the 2019 standard and has many similarities to the US steel design manual AISC 360-16 Ch. C Direct Analysis Method.
Geometric Nonlinearities
Geometric nonlinearities, or second-order effects, are addressed in O.2.2 [1]. Like the simplified method, a second-order analysis can be carried out directly, which includes the effects of loads acting at members' displaced points of intersections (P-Δ effects). Additionally, the effects of axial loads acting on the deflected member shape along the length should be considered (P-δ). Provisions are given in O.2.2 [1] where P-δ can be neglected entirely. On the other hand, if P-δ is included directly in the analysis, the factor U1 can be set to 1.0 used in Clause 13.8 - Axial compression and bending member design [1].
Geometric Imperfections
Member geometric imperfections such as member out-of-straightness or local geometric imperfections such as element out-of-straightness for members do not need to be considered when designing to Clause O.2 [1]. However, global geometric imperfections should be considered with direct modeling or with the use of notional lateral loads. There is the exception, though, that these global geometric imperfections can be neglected for lateral load combinations only if they meet the requirements set forth in Clause O.2.3.1 [1]. The requirements include that the structure's gravity loads are supported primarily by vertical structural elements and the ratio between maximum 2nd-order story drift to 1st-order story drift using reduced member stiffness according to Clause O.2.4 [1] does not exceed 1.7 at any story level.
When the engineer cannot neglect these imperfections, the first method of direct modeling can be used. Member points of intersection should be displaced from their original locations. The amplitude of this initial displacement is set forth in Clause 29.3 [1] and applied in the greatest destabilizing direction, which for most building structures is a 1/500 tolerance for column out-of-plumbness. The significant problem with this method is the high number of model scenarios that must be considered. Theoretically, four displacements are needed in the four different directions at each story level. If member out-of-straightness effects are also coupled with column out-of-plumbness, this adds many more modeling scenarios to be considered to meet the greatest destabilizing effect.
The alternative and preferred method for global geometric imperfections is to apply notional lateral loads. This method is only permitted when the gravity loads are primarily supported by vertical structural elements. Notional lateral loads were covered earlier in this article and are applied in the same manner as the simplified stability analysis in Clause 8.4.3.2 [1]. However, the amplitude is reduced from 0.005 to 0.002 times the factored gravity load at the relevant story. The reduction in magnitude is permitted in Clause O.2.3.3, as these notional loads account for global geometric imperfections only, whereas notional loads in Clause 8.4.3.2 [1] are also accounting for inelasticity effects and other uncertainties.
Inelasticity Effects
To account for inelasticity effects and to also give consideration for initial member or local geometric imperfections as well as uncertainty in stiffness and strength, reduced member axial and flexural stiffness according to the following equations in Clause O.2.4 [1] should be applied to members contributing to the lateral stability.
(E A)r = 0.8 τb E A
(E I)r = 0.8 τb E I
Where,
Cf / Cy < 0.5 ; τb = 1.0
Cf / Cy > 0.5 ; τb = 4
Cf / Cy (1 - Cf / Cy)
To avoid localized distortions, the standard suggests applying this stiffness reduction to all members. Furthermore, when the shear stiffness (GA) and torsional stiffness (GJ) contribute significantly to the lateral stability, stiffness reduction should be considered. Stiffness reduction should not be used when analyzing drifts, deflections, vibrations, or natural vibrations.
Annex O.2 Application in RFEM
The FEA program RFEM has incorporated the latest stability requirements of the CSA S16:19 standard according to the new Annex O.2 provisions.
Geometric Nonlinearities
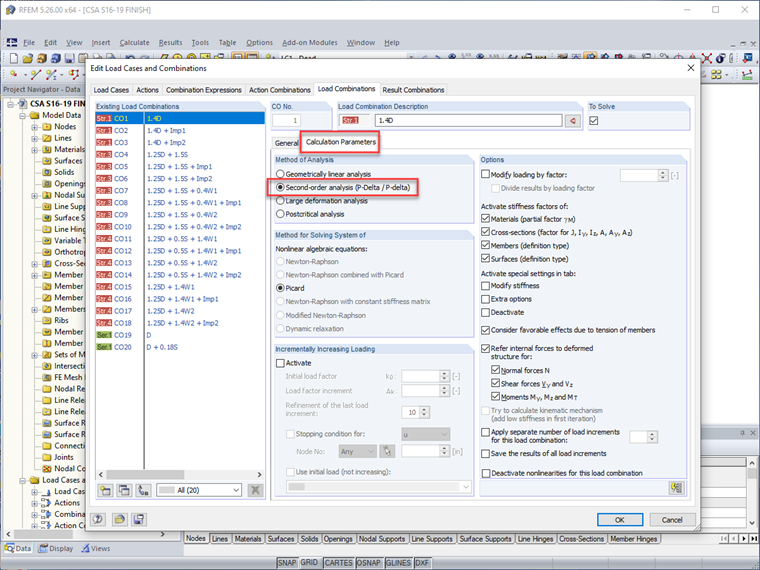
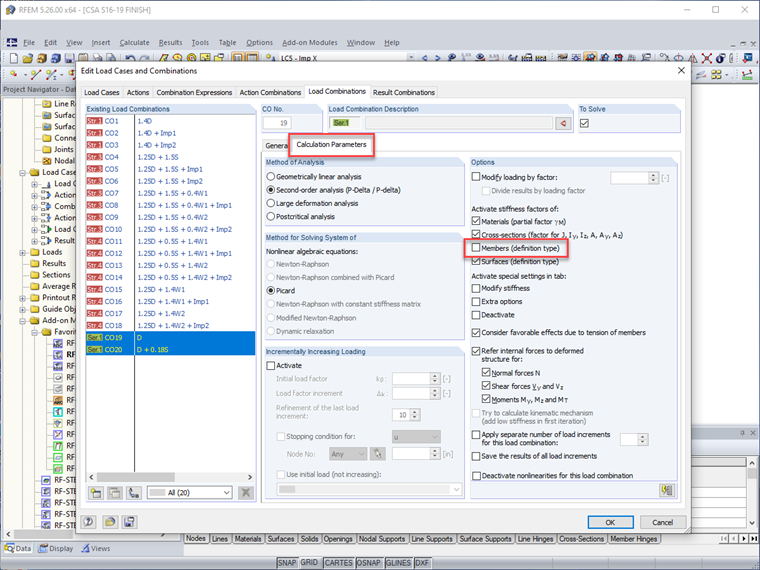
Second-order effects set forth in Clause O.2.2 [1] are directly considered for every load case or load combination when the calculation method is set to "second-order analysis".
Not only are P-Delta effects included for the member analysis, but P-δ are also considered. Therefore, the factor U1 can be set to 1.0 specified in Clause 13.8 directly in the RF-/STEEL CSA member design module.
Geometric Imperfections
The RFEM user has the option to directly model global geometric imperfections by displacing points or nodes of member intersections. However, to ensure this method creates the greatest destabilizing effect, multiple models with various scenarios will need to be carried out. This is rather time-consuming and cumbersome.
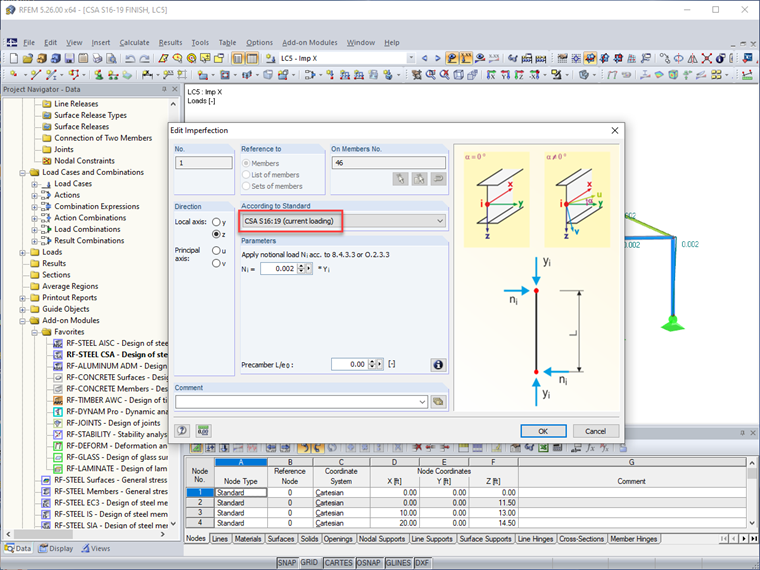
The alternative approach is to apply notional loads with the imperfection options within RFEM. This dialog box now includes the CSA S16:19 in the dropdown options. The notional load is applied to the member end (that is, top of column) with a magnitude equal to 0.002 (or 0.005 if using the simplified stability method) multiplied by the member's axial force (applied member gravity load). An equal and opposite force is internally applied at the opposite member end to avoid unrealistic base shears of the structure.
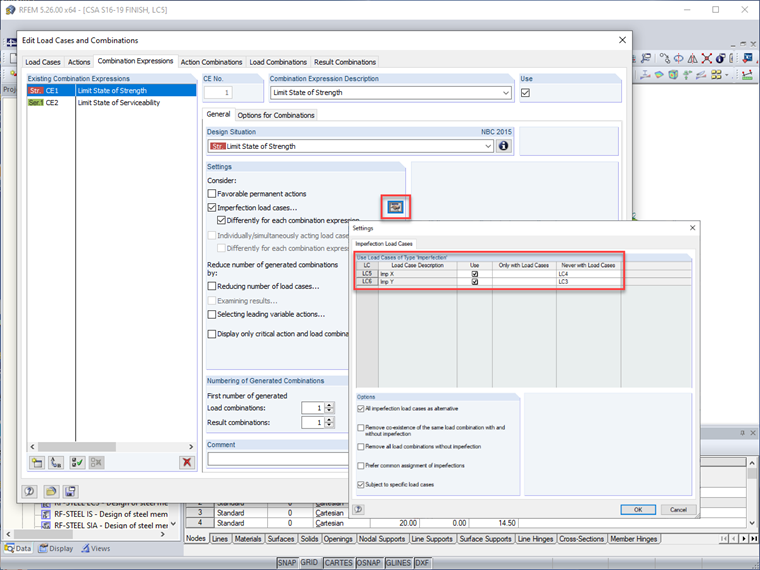
These imperfection load cases can be applied in RFEM with specific lateral load cases to produce the greatest destabilizing action while avoiding the generation of load combinations which will not be controlling and will further increase calculation time (that is, notional loads in the X-direction should only be applied with wind loads in the X-direction). Additionally, imperfections can be turned off completely for load combination expressions such as serviceability while still applied to strength combinations.
Inelasticity Effects
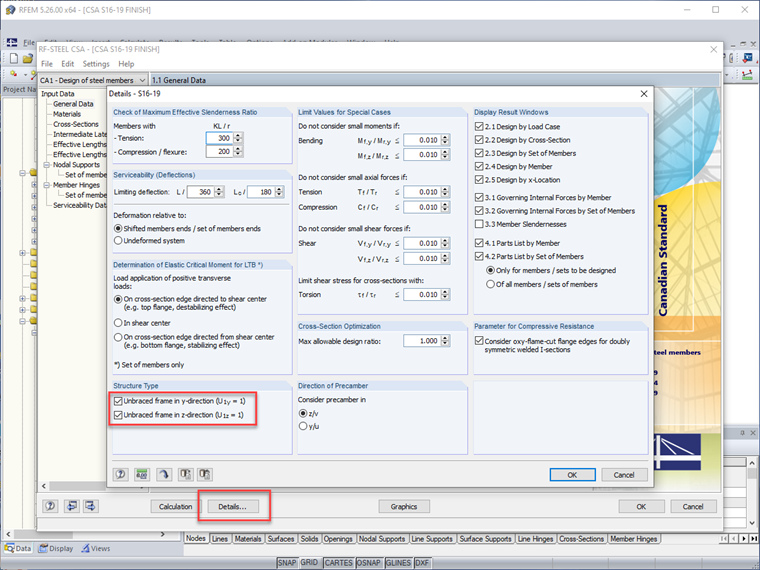
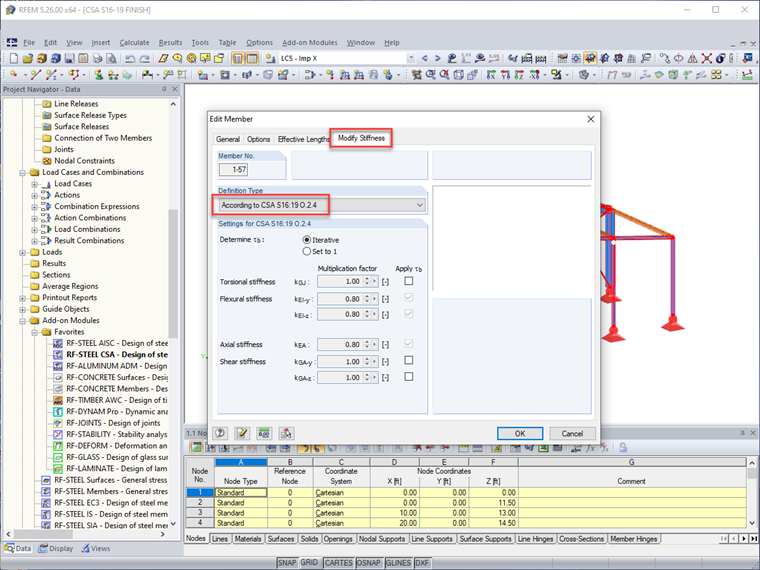
The modify stiffness tab for members now includes the CSA S16:19 standard. When this option is selected, the modification factor 0.8 and the calculated τb factor is applied directly to the member's flexural and axial stiffness. Users also have the option to further apply these reductions to the member's torsional and shear stiffness.
Because member stiffness reduction should not be considered for serviceability design (that is, deflections), RFEM allows users to turn off all member stiffness modifications for serviceability load combinations while leaving this active for strength load combinations.
Summary
Significant stability design updates according to Annex O.2 in the latest Canadian steel design manual CSA S16:19 are now fully incorporated in the RFEM analysis workflow. These updates most significantly include the ability to consider notional loads as imperfections, as well as reduced member stiffnesses according to the CSA S16:19. To see these new updates demonstrated in a detailed example video, check out the webinar CSA S16:19 Steel Design in RFEM.