In Abschnitt 8.4.1 werden die Stabilitätsanforderungen aufgeführt, die bei der Tragwerksplanung unter Verwendung einer der beiden Methoden berücksichtigt werden sollten. Dazu gehören Verformungen, die zur Struktur beitragen, sowie Einflüsse aus Theorie II. Ordnung einschließlich P-Δ und P-δ, globale und geometrische Imperfektionen von Stäben, Steifigkeitsreduktion unter Berücksichtigung von Stabfließen und Restspannungen sowie Unsicherheiten hinsichtlich der Steifigkeit und Festigkeit der Struktur.
Abschnitt 8.4.3 – Vereinfachte Stabilitätsanalyse
Mit der in 8.4.3 [1] angegebenen vereinfachten Stabilitätsanalyse-Methode werden nur einige wenige Anforderungen aufgeführt.
Geometrische Nichtlinearitäten
Die erste umfasst die Einflüsse aus Theorie II. Diese Ordnung für Stäbe oder P-Δ kann direkt in der Analyse berücksichtigt werden. Eine Berechnungsmethode nach Theorie II. Ordnung ist heute bei vielen Statikprogrammen am weitesten verbreitet. Eine Alternative besteht darin, alle axialen Lasten und Biegemomente der Stäbe, die aus einer Analyse nach Theorie I. Ordnung gewonnen wurden, mit dem in 8.4.3.2(b) definierten Faktor U₂ zu verstärken. Dieser Ansatz eignet sich möglicherweise besser für Handberechnungen oder wenn die statische Berechnung die P-Δ-Einflüsse nicht automatisch berücksichtigt.
Geometrische Imperfektionen
Fiktive seitliche Lasten sind der zweite Punkt, der unter der vereinfachten Methode in Abschnitt 8.4.3.3 aufgeführt ist. Diese aufgebrachte Last entspricht dem 0,005-fachen der gesamten, in dem betreffenden Geschoss berücksichtigten Schwerkraftlast und sollte ähnlich wie diese verteilt werden. Fiktive Lasten werden immer in der Richtung aufgebracht, die den größten destabilisierenden Effekt erzeugt. Das bedeutet, dass sie in derselben Richtung wie eine seitliche Windlast aufgebracht werden sollten, um die größten Verformungen und inneren Kräfte in der Struktur zu erzeugen.
Anhang O.2 – Stabilitätswirkungen in der elastischen Analyse
Als Alternative zum oben beschriebenen vereinfachten Ansatz zur Stabilitätsanalyse können Ingenieure Anhang O.2 verwenden, um die in Abschnitt 8.4.1 [1] festgelegten Stabilitätsanforderungen zu erfüllen. Dieser Ansatz wurde 2019 in die Norm aufgenommen und weist viele Ähnlichkeiten mit der Kap. C "Direct Analysis Method" aus dem amerikanischen Stahlkonstruktionshandbuch AISC 360-16 auf.
Geometrische Nichtlinearitäten
Geometrische Nichtlinearitäten oder Einflüsse aus Theorie II. Ordnung werden in O.2.2 [1] behandelt. Wie bei der vereinfachten Methode kann eine Analyse nach Theorie II. Ordnung direkt durchgeführt werden, wobei die Auswirkungen von Lasten berücksichtigt werden, die an den verschobenen Schnittpunkten der Stäbe wirken (P-Δ-Einflüsse). Zusätzlich sollten die Auswirkungen von Axialkräften berücksichtigt werden, die auf die durchgebogene Bauteilform entlang ihrer Länge wirken (P-δ). In O.2.2 [1] sind Bestimmungen enthalten, nach denen P-δ ganz vernachlässigt werden kann. Wird P-δ hingegen direkt in die Analyse einbezogen, kann der Faktor U1 auf 1,0 gesetzt werden, wie in Abschnitt 13.8 – Bemessung von Stäben für axiale Druck- und Biegebelastungen [1] verwendet.
Geometrische Imperfektionen
Geometrische Imperfektionen von Stäben, wie z. B. die Schiefheit von Stäben, oder lokale geometrische Imperfektionen, wie z. B. die Schiefheit von Elementen für Stäbe, müssen bei der Bemessung gemäß Abschnitt O.2 [1] nicht berücksichtigt werden. Globale geometrische Imperfektionen sollten jedoch bei der direkten Modellierung oder unter Verwendung von fiktiven Querkräften berücksichtigt werden. Es gibt jedoch eine Ausnahme: Diese globalen geometrischen Imperfektionen können bei seitlichen Lastkombinationen nur dann vernachlässigt werden, wenn sie die in Abschnitt O.2.3.1 [1] festgelegten Anforderungen erfüllen. Zu den Anforderungen gehört, dass die Schwerkraftlasten der Struktur in erster Linie von vertikalen Stäben getragen werden und das Verhältnis zwischen der maximalen Verschiebung des Geschosses nach Theorie II. Ordnung und der Verschiebung des Geschosses nach Theorie I. Ordnung unter Verwendung der reduzierten Stabsteifigkeit gemäß Abschnitt O.2.4 [1] in keinem Geschoss den Wert 1,7 überschreitet.
Wenn der Ingenieur diese Imperfektionen nicht vernachlässigen kann, kann die erste Methode der direkten Modellierung verwendet werden. Die Schnittpunkte der Stäbe sollten von ihren ursprünglichen Positionen verschoben werden. Die Amplitude dieser anfänglichen Verschiebung ist in Abschnitt 29.3 [1] festgelegt und wird in der Richtung mit der größten Destabilisierung angewendet. Für die meisten Gebäude bedeutet dies eine Toleranz von 1/500 für die Schieflage von Stützen. Das wesentliche Problem bei dieser Methode ist die hohe Anzahl von Modellszenarien, die berücksichtigt werden müssen. Theoretisch sind auf jedem Geschoss vier Verschiebungen in vier verschiedenen Richtungen erforderlich. Gehen die Auswirkungen der Schieflage der Stäbe mit einer Schieflage der Stützen einher, müssen viele weitere Modellierungsszenarien berücksichtigt werden, um den destabilisierenden Effekt zu maximieren.
Die alternative und bevorzugte Methode für globale geometrische Imperfektionen ist die Anwendung von fiktiven Querlasten. Diese Methode ist nur zulässig, wenn die Schwerkraftlasten hauptsächlich von vertikalen Strukturelementen getragen werden. Fiktive Querlasten wurden bereits weiter oben in diesem Artikel behandelt und werden auf die gleiche Weise wie bei der vereinfachten Stabilitätsanalyse in Abschnitt 8.4.3.2 [1] angewendet. Die Amplitude wird jedoch von 0,005 auf das 0,002-fache der faktorisierten Schwerkraftlast im entsprechenden Geschoss reduziert. Die Reduzierung der Größe ist gemäß Abschnitt O.2.3.3 zulässig, da diese fiktiven Lasten nur globale geometrische Imperfektionen berücksichtigen, während fiktive Lasten gemäß Abschnitt 8.4.3.2 [1] auch Auswirkungen der Nichtelastizität und andere Unbestimmtheiten berücksichtigen.
Auswirkungen der Nichtelastizität
Um die Auswirkungen der Nichtelastizität sowie anfängliche oder lokale geometrische Imperfektionen der Stäbe und Unbestimmtheiten bezüglich Steifigkeit und Festigkeit zu berücksichtigen, sollte für Stäbe, die zur seitlichen Stabilität beitragen, eine reduzierte axiale Steifigkeit und Biegesteifigkeit gemäß den in Abschnitt O.2.4 [1] aufgeführten Gleichungen verwendet werden.
(E A)r = 0.8 τb E A
(E I)r = 0.8 τb E I
Wobei,
Cf / Cy < 0.5 ; τb = 1.0
Cf / Cy > 0.5 ; τb = 4
Cf / Cy (1 - Cf / Cy)
Um lokale Verformungen zu vermeiden, empfiehlt die Norm, diese Steifigkeitsreduzierung auf alle Stäbe anzuwenden. Wenn die Schubsteifigkeit (GA) und die Torsionssteifigkeit (GJ) erheblich zur seitlichen Stabilität beitragen, sollte eine Steifigkeitsreduzierung in Betracht gezogen werden. Bei der Analyse von Verschiebungen, Durchbiegungen, Schwingungen oder Eigenfrequenzen sollte keine Steifigkeitsreduzierung angewendet werden.
Anhang O.2 Anwendung in RFEM
Das FEA-Programm RFEM hat die neuesten Stabilitätsanforderungen der Norm CSA S16:19 gemäß den neuen Bestimmungen des Anhangs O.2 integriert.
Geometrische Nichtlinearitäten
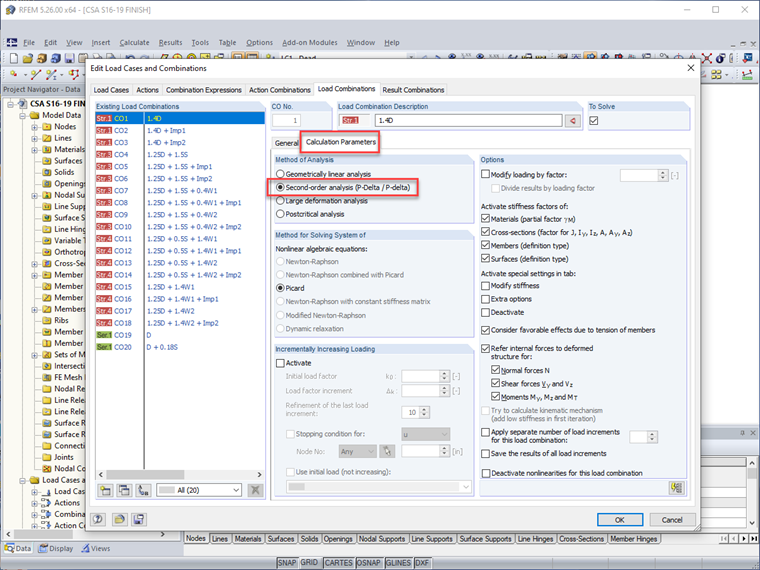
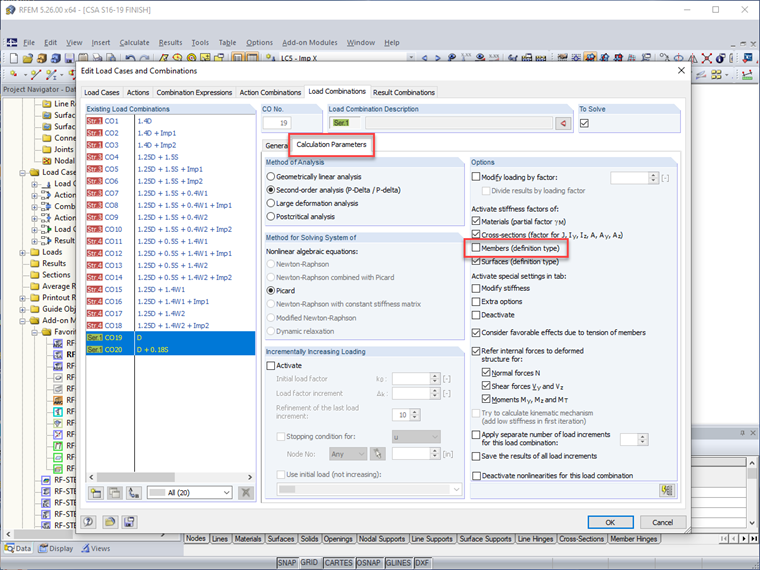
Die in Abschnitt O.2.2 [1] dargelegten Einflüsse aus Theorie II. Ordnung werden für jeden Lastfall oder jede Lastkombination direkt berücksichtigt, wenn die Berechnungsmethode auf "Theorie II. Ordnung" eingestellt ist.
Für die Stabberechnung werden nicht nur P-Delta-Effekte, sondern auch P-δ berücksichtigt. Daher kann der Faktor U1 im Modul RF-/STEEL CSA für die Stabbemessung gemäß Abschnitt 13.8 direkt auf 1,0 gesetzt werden.
Geometrische Imperfektionen
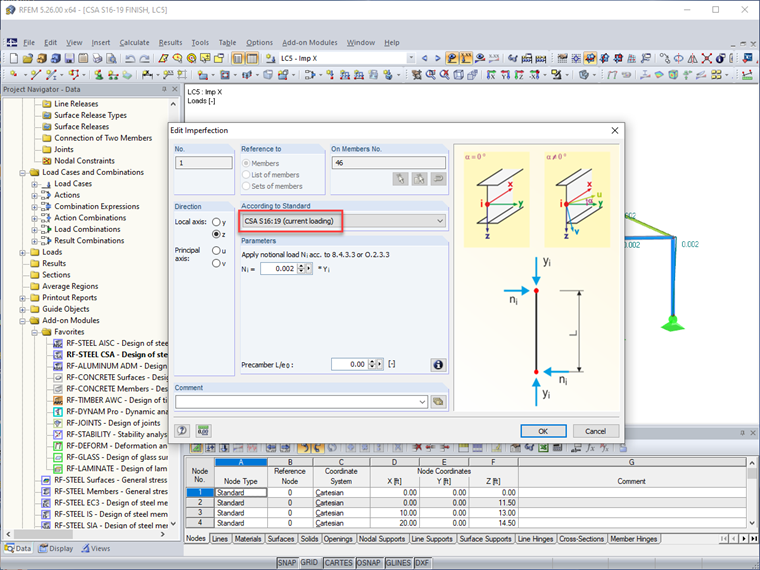
RFEM-Anwender haben die Möglichkeit, globale geometrische Imperfektionen direkt zu modellieren, indem sie Punkte oder Knoten von Stabschnittstellen verschieben. Um jedoch sicherzustellen, dass diese Methode den größten destabilisierenden Effekt erzielt, müssen mehrere Modelle mit verschiedenen Szenarien erstellt werden. Dies ist jedoch ziemlich zeitaufwändig und umständlich.
Eine alternative Vorgehensweise besteht darin, fiktive Lasten mit den Imperfektionsoptionen in RFEM anzuwenden. In den Dropdown-Optionen dieses Dialogfelds ist nun CSA S16:19 enthalten. Die fiktive Last wird mit einer Größe von 0,002 (bzw. 0,005 bei Verwendung der vereinfachten Stabilitätsmethode) auf das Stabende (d. h. die Oberseite der Stütze) aufgebracht, und zwar multipliziert mit der Normalkraft des Stabs (d. h. der angewandten Schwerkraftlast des Stabs). Um unrealistische Basisschubkräfte der Struktur zu vermeiden, wird eine gleiche und entgegengesetzte Kraft intern am gegenüberliegenden Stabende aufgebracht.
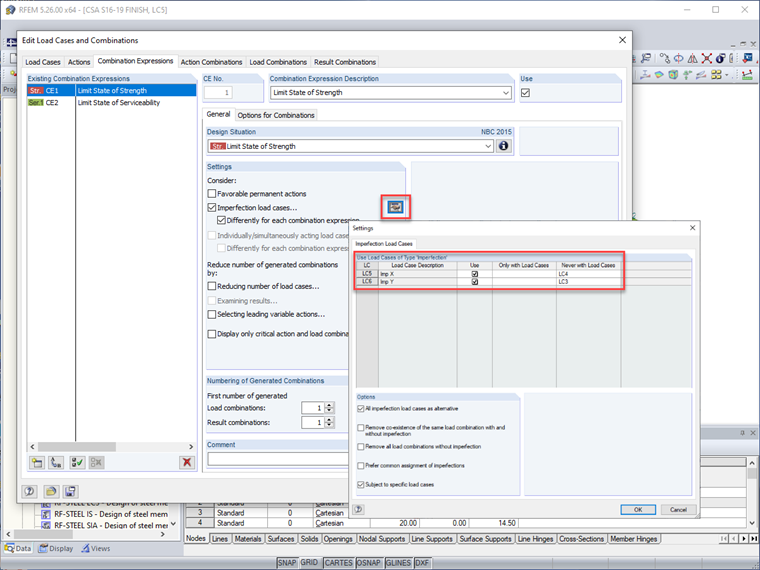
Diese Lastfälle für Imperfektionen können in RFEM mit spezifischen seitlichen Lastfällen angewendet werden, um die größte destabilisierende Wirkung zu erzeugen. Gleichzeitig wird die Generierung von nicht maßgeblichen Lastkombinationen vermieden, die die Berechnungszeit unnötig verlängern würden (d. h. fiktive Lasten in X-Richtung sollten nur mit Windlasten in X-Richtung angewendet werden). Darüber hinaus können Imperfektionen für Ausdrücke von Lastkombinationen, beispielsweise für die Gebrauchstauglichkeit, vollständig deaktiviert werden, während sie für Festigkeitskombinationen weiterhin angewendet werden.
Auswirkungen der Nichtelastizität
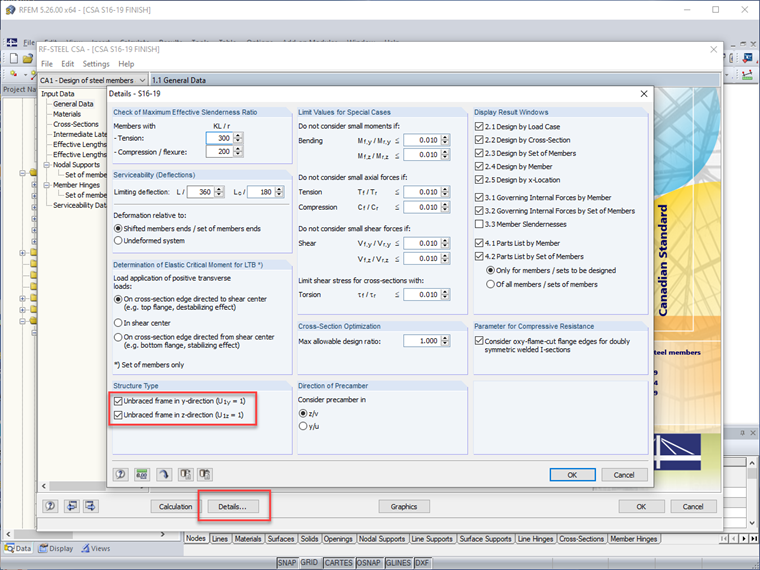
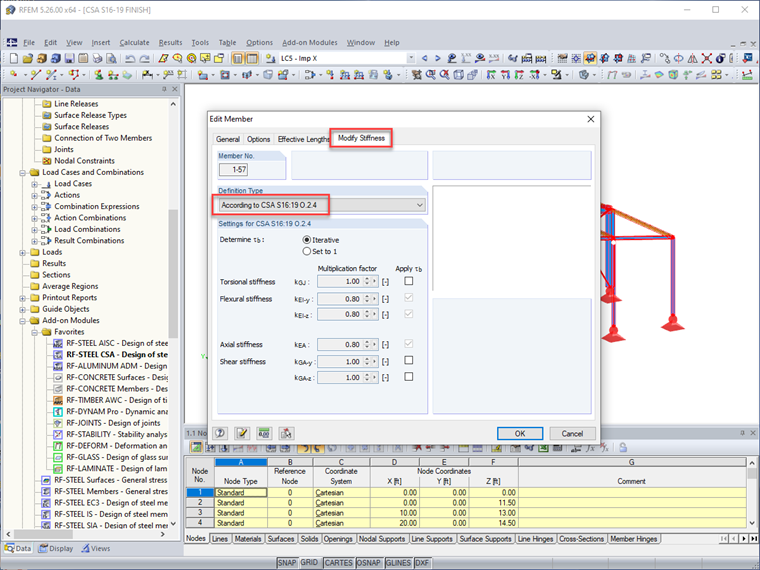
Die Option "Steifigkeit ändern" für Stäbe enthält nun die Norm CSA S16:19. Ist diese Option ausgewählt, werden der Modifikationsfaktor 0,8 und der berechnete τb-Faktor direkt auf die Biege- und Axialsteifigkeit des Stabs angewendet. Benutzer haben außerdem die Möglichkeit, diese Reduzierungen zusätzlich auf die Torsions- und Schubsteifigkeit des Stabs anzuwenden.
Da die Reduzierung der Stabsteifigkeit bei der Bemessung der Gebrauchstauglichkeit (d. h. der Durchbiegungen) keine Rolle spielt, bietet RFEM die Möglichkeit, alle Änderungen der Stabsteifigkeit für die Lastkombinationen der Gebrauchstauglichkeit zu deaktivieren. Für die Lastkombinationen der Tragfähigkeit bleiben diese Änderungen hingegen aktiv.
Fazit
Die wichtigen Aktualisierungen der Stabilitätsbemessung gemäß Anhang O.2 der neuesten kanadischen Norm für Stahlbemessung CSA S16:19 sind nun vollständig in den Arbeitsablauf der RFEM-Analyse integriert. Zu diesen Aktualisierungen gehört vor allem die Möglichkeit, fiktive Lasten als Imperfektionen sowie reduzierte Stabsteifigkeiten gemäß CSA S16:19 zu berücksichtigen. Um diese neuen Aktualisierungen in einem detaillierten Beispielvideo zu sehen, schauen Sie sich das Webinar CSA S16:19 Stahlbemessung in RFEM an.