A cláusula 8.4.1 [1] lista os requisitos de estabilidade que o dimensionamento estrutural deve abordar usando qualquer um dos métodos. Estes incluem deformações que contribuem para a estrutura, efeitos de segunda ordem, incluindo P-Δ e P-δ, imperfeições geométricas globais e de barras, redução de rigidez considerando a cedência da barra e tensões residuais, e por fim, incerteza na rigidez e resistência da estrutura.
Cláusula 8.4.3 – Método de análise de estabilidade simplificado
Com o método de análise de estabilidade simplificado dado em 8.4.3 [1], apenas alguns requisitos são listados.
Não-linearidades geométricas
A primeira inclui efeitos de segunda ordem das barras, ou P-Δ, que podem ser considerados diretamente na análise. O método de cálculo de análise de segunda ordem é mais comum com muitos dos programas de análise estrutural hoje em dia. A alternativa é amplificar todas as cargas axiais e momentos fletores das barras obtidos a partir de uma análise de primeira ordem pelo fator U2 definido em 8.4.3.2(b) [1]. Esta abordagem pode ser mais apropriada para cálculos manuais ou se o software de análise estrutural não incluir automaticamente os efeitos de P-Δ.
Imperfeições geométricas
Cargas laterais fictícias são o segundo item listado sob o método simplificado na Cláusula 8.4.3.3 [1]. Esta carga aplicada é igual a 0,005 vezes a sobrecarga total fatorizada no andar considerado e deve ser distribuída de forma similar à sobrecarga. Cargas fictícias são sempre aplicadas na direção que gera o maior efeito desestabilizador. Isso significa que tais cargas devem ser aplicadas na mesma direção de uma carga de vento lateral para gerar as maiores deformações e forças internas na estrutura.
Anexo O.2 – Efeitos de estabilidade na análise elástica
Como alternativa à abordagem da análise de estabilidade simplificada acima, engenheiros podem utilizar o Anexo O.2 para cumprir os requisitos de estabilidade estabelecidos na Cláusula 8.4.1 [1]. Esta abordagem foi adicionada à norma de 2019 e tem muitas semelhanças com o manual de dimensionamento de aço dos EUA AISC 360-16 Cap. C Método de Análise Direta.
Não-linearidades geométricas
Não-linearidades geométricas, ou efeitos de segunda ordem, são abordados em O.2.2 [1]. Como o método simplificado, uma análise de segunda ordem pode ser realizada diretamente, o que inclui os efeitos de cargas que atuam nos pontos de interseção deslocados das barras (efeitos de P-Δ). Adicionalmente, devem ser considerados os efeitos das cargas axiais atuando na forma da barra deslocada ao longo do seu comprimento (P-δ). As disposições são dadas em O.2.2 [1] onde P-δ pode ser totalmente negligenciado. Por outro lado, se P-δ estiver incluído diretamente na análise, o fator U1 pode ser definido como 1,0 usado na Cláusula 13.8 - Dimensionamento da barra de compressão axial e flexão [1].
Imperfeições geométricas
As imperfeições geométricas das barras, como a curvatura ou imperfeições geométricas locais para barras, não precisam ser consideradas ao dimensionar segundo a Cláusula O.2 [1]. Entretanto, as imperfeições geométricas globais devem ser consideradas com a modelação direta ou com o uso de cargas laterais fictícias. Há a exceção, contudo, de que essas imperfeições geométricas globais podem ser negligenciadas para combinações de carga lateral apenas se cumprirem os requisitos estabelecidos na Cláusula O.2.3.1 [1]. Os requisitos incluem que sobrecarga da estrutura são suportadas principalmente por elementos estruturais verticais e a proporção entre o máximo deslocamento de segunda ordem e o deslocamento de primeira ordem usando a rigidez reduzida das barras de acordo com a Cláusula O.2.4 [1] não excede 1,7 em qualquer andar.
Quando o engenheiro não pode negligenciar essas imperfeições, pode ser utilizado o primeiro método de modelação direta. Os pontos de interseção das barras devem ser deslocados de suas localizações originais. A amplitude desse deslocamento inicial é estabelecida na Cláusula 29.3 [1] e aplicada na direção de maior desestabilização, que para a maioria das estruturas de edifícios é uma tolerância de 1/500 para a inclinação dos pilares. O principal problema com este método é o elevado número de cenários de modelo que devem ser considerados. Teoricamente, são necessários quatro deslocamentos nas quatro diferentes direções em cada andar. Se os efeitos da inclinação das barras também forem combinados com a inclinação dos pilares, isso adiciona muitos mais cenários de modelação a serem considerados para atingir o maior efeito desestabilizador.
O método alternativo e preferido para as imperfeições geométricas globais é aplicar cargas laterais fictícias. Este método é permitido apenas quando as sobrecargas são suportadas principalmente por elementos estruturais verticais. As cargas laterais fictícias foram abordadas anteriormente neste artigo e são aplicadas da mesma maneira como para a análise de estabilidade simplificada na Cláusula 8.4.3.2 [1]. No entanto, a amplitude é reduzida de 0,005 para 0,002 vezes a sobrecarga fatorizada no andar relevante. A redução na magnitude é permitida na Cláusula O.2.3.3, já que essas cargas fictícias consideram apenas para imperfeições geométricas globais, enquanto as cargas fictícias na Cláusula 8.4.3.2 [1] também contabilizam os efeitos de inelasticidade e outras incertezas.
Efeitos de inelasticidade
Para considerar os efeitos de inelasticidade e também considerar as imperfeições geométricas iniciais das barras ou locais, bem como a incerteza na rigidez e resistência, rigidez axial e de flexão reduzida das barras de acordo com as seguintes equações na Cláusula O.2.4 [1] deve ser aplicada às barras que contribuem para a estabilidade lateral.
(E A)r = 0,8 τb E A
(E I)r = 0,8 τb E I
Onde,
Cf / Cy < 0,5 ; τb = 1,0
Cf / Cy > 0,5 ; τb = 4
Cf / Cy (1 - Cf / Cy)
Para evitar distorções localizadas, a norma sugere aplicar essa redução de rigidez a todos as barras. Além disso, quando a rigidez de corte (GA) e a rigidez à torção (GJ) contribuem significativamente para a estabilidade lateral, deve ser considerada a redução de rigidez. A redução de rigidez não deve ser usada ao analisar desvios, deformações, vibrações ou vibrações naturais.
Aplicação do anexo O.2 no RFEM
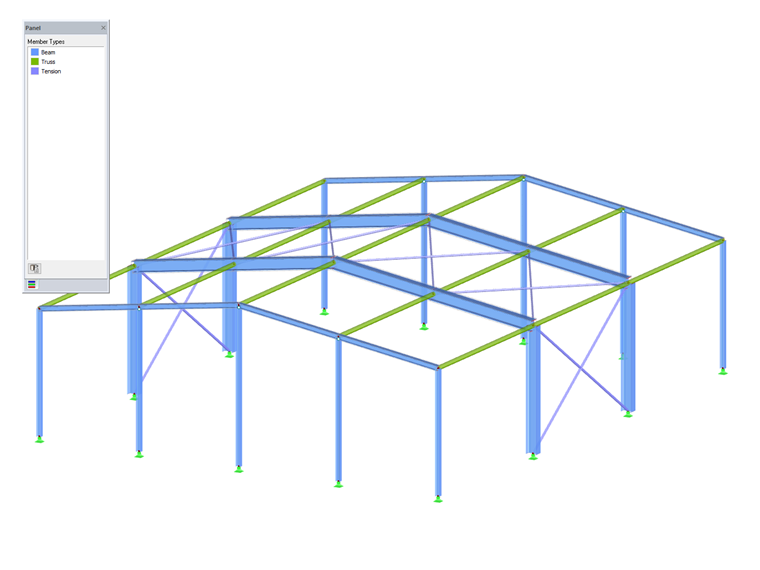
O programa FEA RFEM incorporou os últimos requisitos de estabilidade da norma CSA S16:19 de acordo com as novas disposições do Anexo O.2.
Não-linearidades geométricas
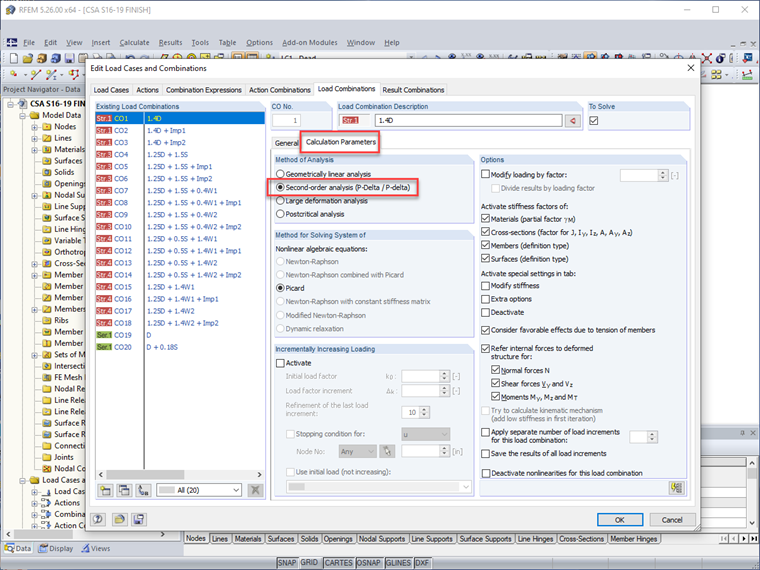
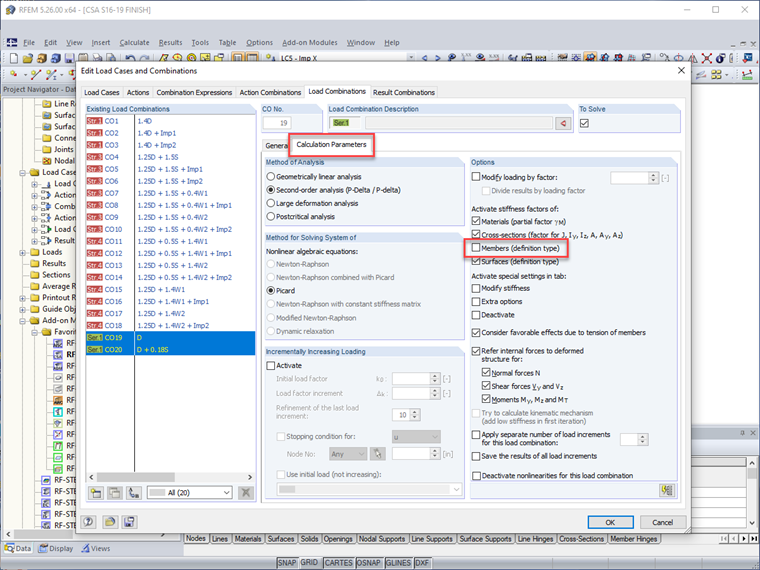
Os efeitos de segunda ordem estabelecidos na Cláusula O.2.2 [1] são considerados diretamente para cada caso de carga ou combinação de carga quando o método de cálculo é configurado para a "análise de segunda ordem".
Não apenas os efeitos P-Delta estão incluídos para a análise das barras, mas também são considerados P-δ. Portanto, o fator U1 pode ser definido como 1,0 especificado na Cláusula 13.8 diretamente no módulo de dimensionamento de barras RF-/STEEL CSA.
Imperfeições geométricas
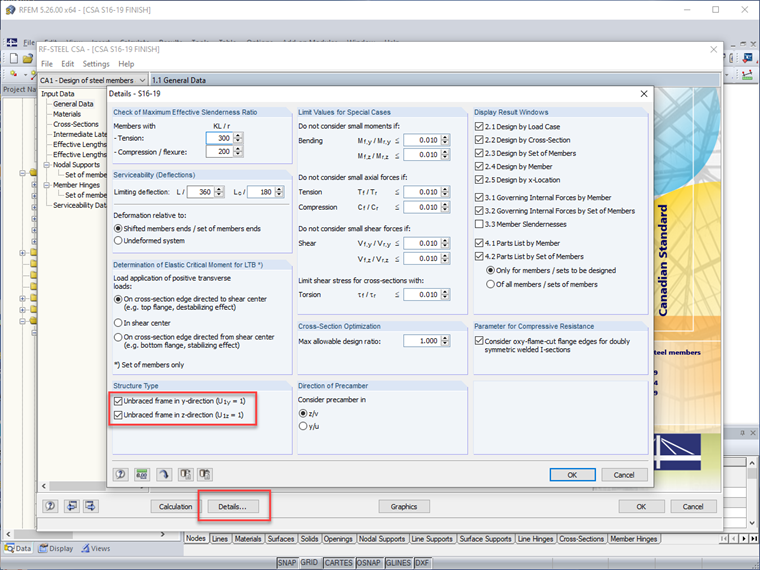
O utilizador do RFEM tem a opção de modelar diretamente imperfeições geométricas globais através do deslocando pontos ou nós das interseções das barras. No entanto, para garantir que este método crie o maior efeito desestabilizador, são realizados múltiplos modelos com vários cenários precisarão. Este processo é bastante demorado e complicado.
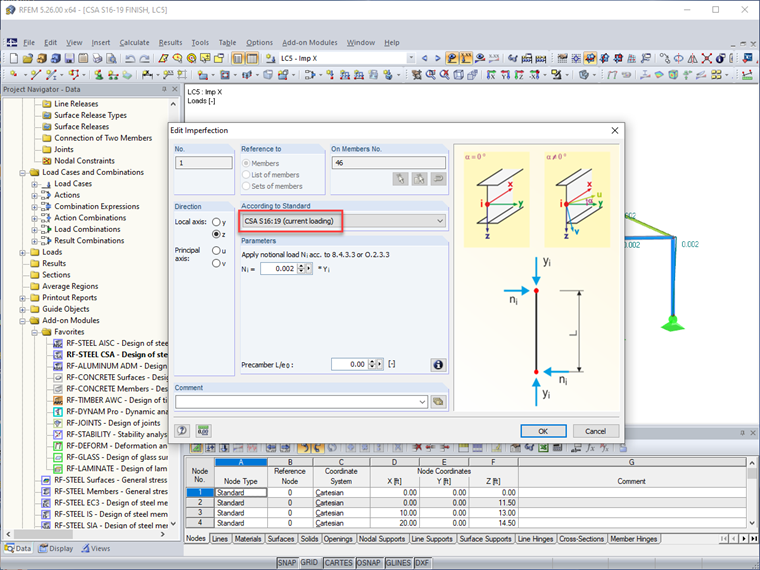
A abordagem alternativa é aplicar cargas fictícias com as opções de imperfeição dentro do RFEM. Esta caixa de diálogo agora inclui a CSA S16:19 nas opções do menu suspenso. A carga fictícia é aplicada à extremidade da barra (ou seja, topo do pilar) com uma magnitude igual a 0,002 (ou 0,005 se utilizar o método de estabilidade simplificado) multiplicada pela força axial da barra (sobrecarga aplicada à barra). Uma força igual e oposta é internamente aplicada na extremidade oposta da barra para evitar forças de corte de base irrealistas da estrutura.
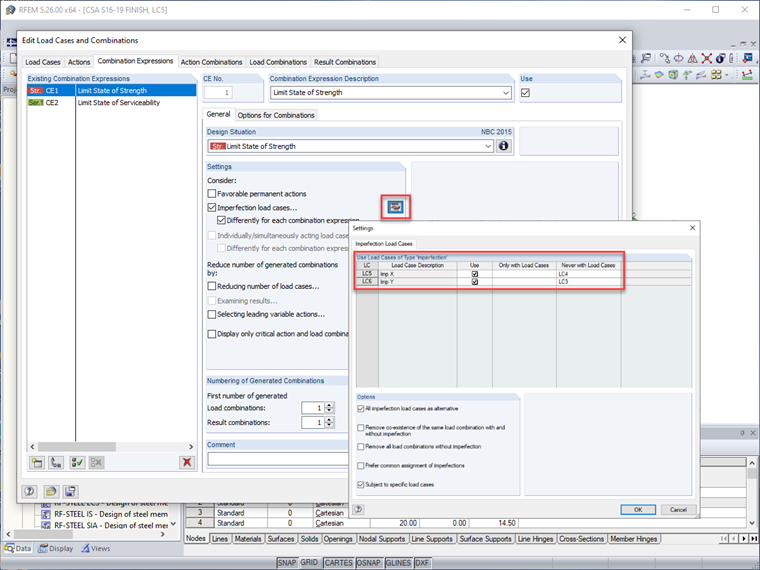
Esses casos de carga de imperfeição podem ser aplicados no RFEM com casos de carga lateral específicos para produzir a maior ação desestabilizadora enquanto evita a geração de combinações de carga que não serão controladoras e aumentarão ainda mais o tempo de cálculo (ou seja, as cargas fictícias na direção X devem ser aplicadas apenas com cargas de vento na direção X). Além disso, as imperfeições podem ser completamente desativadas para as regras de combinação de carga como a utilização, enquanto ainda são aplicadas para as combinações de resistência.
Efeitos de inelasticidade
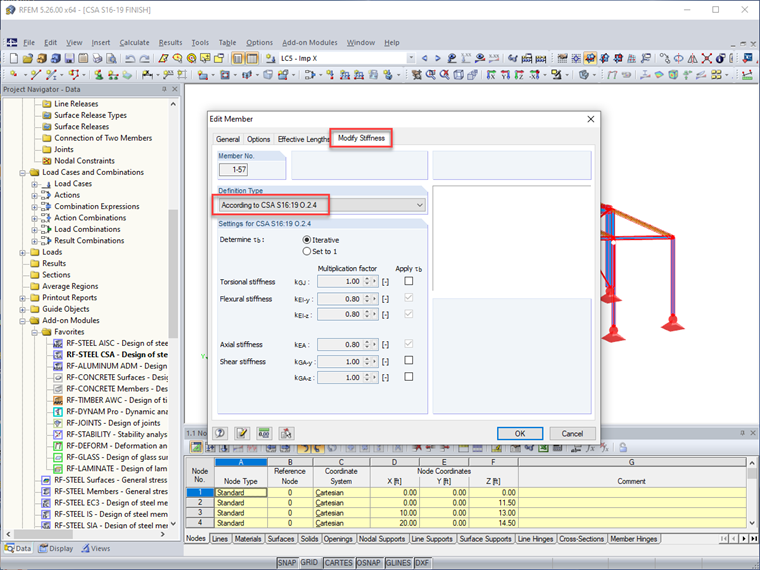
O separador de modificar a rigidez para barras agora inclui a norma CSA S16:19. Quando esta opção é selecionada, o fator de modificação de 0,8 e o fator τb calculado são aplicados diretamente à rigidez de flexão e axial da barra. Os utilizadores também têm a opção de aplicar ainda mais essas reduções à rigidez à torção e ao corte da barra.
Porque a redução de rigidez da barra não deve ser considerada para a verificação ao estado limite de utilização (ou seja, deformações), o RFEM permite aos utilizadores desativar todas as modificações de rigidez das barras para as combinações de carga de para a utilização enquanto deixa isso ativo para combinações de carga de resistência.
Resumo
As significativas atualizações do dimensionamento de estabilidade de acordo com o Anexo O.2 no último manual de dimensionamento de aço canadiano CSA S16:19 encontram-se agora totalmente incorporadas no fluxo de trabalho de análise RFEM. Essas atualizações incluem principalmente a capacidade de considerar cargas fictícias como imperfeições, bem como rigidezes de barras reduzida de acordo com o CSA S16:19. Para ver essas novas atualizações demonstradas num exemplo em vídeo detalhado, consulte o webinar CSA S16:19 Dimensionamento de Aço no RFEM.