Clause 8.4.1 [1] énumère les exigences de stabilité que la conception structurelle doit aborder en utilisant l'une ou l'autre méthode. Celles-ci incluent les déformations contribuant à la structure, les effets du second ordre incluant P-Δ et P-δ, les imperfections géométriques globales et des éléments, la réduction de la rigidité tenant compte de la plastification des éléments et des contraintes résiduelles, et enfin, l'incertitude dans la rigidité et la résistance de la structure.
Clause 8.4.3 – Méthode d'Analyse Simplifiée de Stabilité
Avec la méthode d'analyse simplifiée de stabilité donnée dans 8.4.3 [1], seules quelques exigences sont listées.
Non-linéarités Géométriques
La première inclut les effets du second ordre des éléments, ou P-Δ, qui peuvent être directement pris en compte dans l'analyse. Une méthode de calcul d'analyse de second ordre est la plus courante avec de nombreux programmes de calcul structurel aujourd'hui. L'alternative est d'amplifier toutes les charges axiales des éléments et les moments de flexion obtenus à partir d'une analyse de premier ordre par le facteur U2 défini dans 8.4.3.2(b) [1]. Cette approche peut être mieux adaptée aux calculs manuels, ou si le logiciel de calcul structurel n'inclut pas automatiquement les effets P-Δ.
Imperfections Géométriques
Les charges latérales notionnelles sont le deuxième élément listé dans la méthode simplifiée à la Clause 8.4.3.3 [1]. Cette charge appliquée est égale à 0,005 fois la charge gravitaire totale pondérée à l'étage considéré et doit être distribuée de manière similaire à la charge gravitaire. Les charges notionnelles sont toujours appliquées dans la direction qui génère le plus grand effet déstabilisant. Cela signifie que ces charges doivent être appliquées dans la même direction qu'une charge de vent latérale pour générer les plus grandes déformations et forces internes sur la structure.
Annexe O.2 – Effets de Stabilité dans l'Analyse Élastique
Comme alternative à l'approche d'analyse simplifiée de stabilité ci-dessus, les ingénieurs peuvent utiliser l'Annexe O.2 pour satisfaire aux exigences de stabilité définies à la Clause 8.4.1 [1]. Cette approche a été ajoutée à la norme de 2019 et présente de nombreuses similitudes avec le manuel de conception en acier des États-Unis AISC 360-16 Ch. C Méthode d'Analyse Directe.
Non-linéarités Géométriques
Les non-linéarités géométriques, ou effets du second ordre, sont abordées dans O.2.2 [1]. Comme la méthode simplifiée, une analyse de second ordre peut être réalisée directement, ce qui inclut les effets des charges agissant aux points de rencontre déplacés des éléments (effets P-Δ). De plus, les effets des charges axiales agissant sur la forme déformée de l'élément sur toute sa longueur doivent être pris en compte (P-δ). Des dispositions sont données dans O.2.2 [1] où P-δ peut être complètement négligé. D'autre part, si P-δ est inclus directement dans l'analyse, le facteur U1 peut être réglé sur 1.0 utilisé à la Clause 13.8 - Conception des éléments en compression axiale et en flexion [1].
Imperfections Géométriques
Les imperfections géométriques des éléments telles que le gauchissement d'un élément ou les imperfections géométriques locales comme le gauchissement d'un élément pour des éléments ne doivent pas être prises en compte lors de la conception selon la Clause O.2 [1]. Cependant, les imperfections géométriques globales doivent être prises en compte par la modélisation directe ou par l'utilisation de charges latérales notionnelles. Il existe cependant une exception, ces imperfections géométriques globales peuvent être négligées pour les seules combinaisons de charges latérales si elles remplissent les exigences définies à la Clause O.2.3.1 [1]. Les exigences incluent que les charges gravitaires de la structure sont principalement supportées par des éléments structurels verticaux et que le rapport entre la dérive d'étage de second ordre maximale et la dérive d'étage de premier ordre en utilisant la rigidité réduite des éléments selon la Clause O.2.4 [1] ne dépasse pas 1,7 à aucun niveau d'étage.
Lorsque l'ingénieur ne peut pas négliger ces imperfections, la première méthode de modélisation directe peut être utilisée. Les points d'intersection des éléments doivent être déplacés de leurs emplacements d'origine. L'amplitude de ce déplacement initial est définie à la Clause 29.3 [1] et appliquée dans la direction la plus déstabilisante, ce qui pour la plupart des structures de bâtiment correspond à une tolérance de 1/500 pour le déséquilibre des colonnes. Le problème significatif avec cette méthode est le nombre élevé de scénarios de modélisation qui doivent être considérés. Théoriquement, quatre déplacements sont nécessaires dans les quatre directions différentes à chaque niveau d'étage. Si les effets de gauchissement d'un élément sont également couplés avec le déséquilibre des colonnes, cela ajoute bien plus de scénarios de modélisation à considérer pour atteindre le plus grand effet déstabilisant.
L'alternative et méthode préférée pour les imperfections géométriques globales est d'appliquer des charges latérales notionnelles. Cette méthode est uniquement autorisée lorsque les charges gravitaires sont principalement supportées par des éléments structurels verticaux. Les charges latérales notionnelles ont été abordées plus tôt dans cet article et sont appliquées de la même manière que l'analyse simplifiée de stabilité à la Clause 8.4.3.2 [1]. Cependant, l'amplitude est réduite de 0,005 à 0,002 fois la charge gravitaire pondérée à l'étage pertinent. La réduction en amplitude est permise dans la Clause O.2.3.3, car ces charges notionnelles prennent en compte uniquement les imperfections géométriques globales, tandis que les charges notionnelles à la Clause 8.4.3.2 [1] tiennent également compte des effets d'inhomogénéité et d'autres incertitudes.
Effets d'Inhomogénéité
Pour tenir compte des effets d'inhomogénéité et également pour considérer les imperfections initiales des éléments ou imperfections géométriques locales ainsi que l'incertitude dans la rigidité et la résistance, la rigidité axiale et en flexion réduite des éléments selon les équations suivantes dans la Clause O.2.4 [1] doit être appliquée aux éléments contribuant à la stabilité latérale.
(E A)r = 0.8 τb E A (E I)r = 0.8 τb E I Où, Cf / Cy < 0.5 ; τb = 1.0 Cf / Cy > 0.5 ; τb = 4 Cf / Cy (1 - Cf / Cy)
Pour éviter les distorsions localisées, la norme suggère d'appliquer cette réduction de rigidité à tous les éléments. En outre, lorsque la rigidité en cisaillement (GA) et la rigidité à la torsion (GJ) contribuent de manière significative à la stabilité latérale, il convient de considérer la réduction de rigidité. La réduction de rigidité ne doit pas être utilisée lors de l'analyse des dérives, des déformations, des vibrations ou des vibrations naturelles.
Application de l'Annexe O.2 dans RFEM
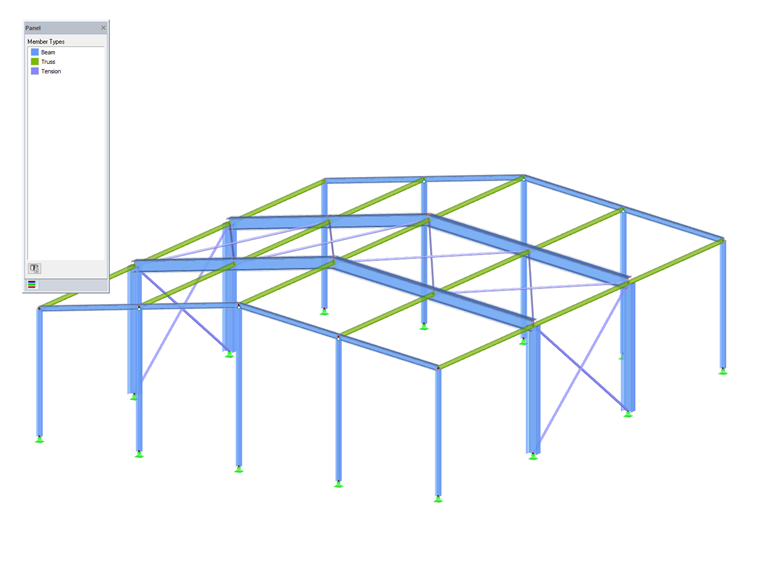
Le programme EF RFEM a intégré les dernières exigences de stabilité de la norme CSA S16:19 selon les nouvelles dispositions de l'Annexe O.2.
Non-linéarités Géométriques
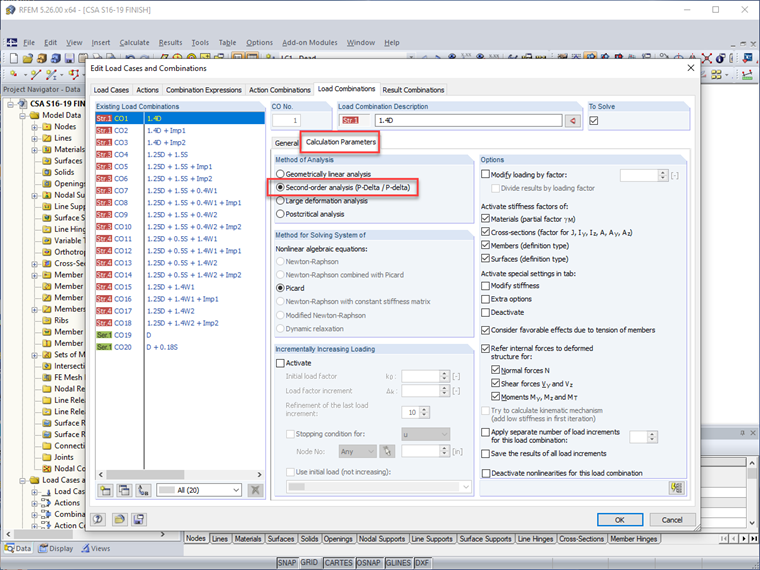
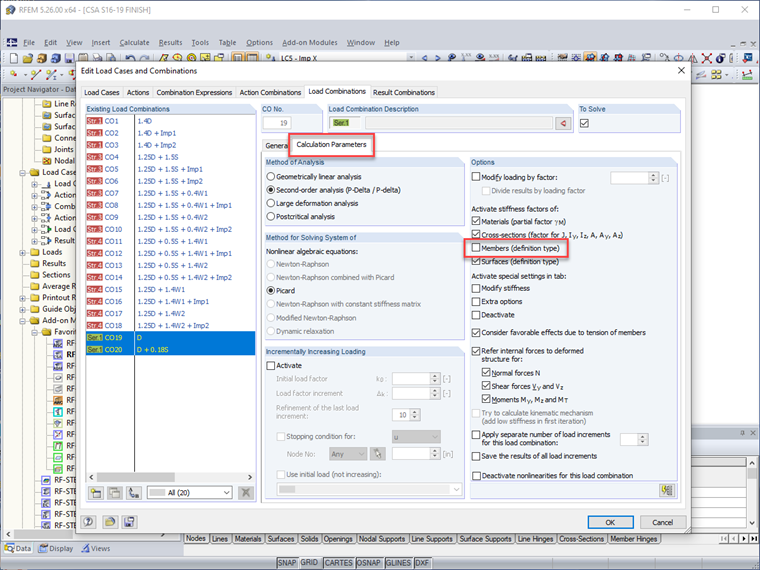
Les effets de second ordre définis à la Clause O.2.2 [1] sont directement pris en compte pour chaque cas de charge ou combinaison de charges lorsque la méthode de calcul est définie sur "analyse de second ordre".
Non seulement les effets P-Delta sont inclus pour l'analyse des éléments, mais P-δ est aussi pris en compte. Par conséquent, le facteur U1 peut être réglé sur 1.0 spécifié à la Clause 13.8 directement dans le module de conception des éléments RF-/STEEL CSA.
Imperfections Géométriques
L'utilisateur de RFEM a la possibilité de modéliser directement les imperfections géométriques globales en déplaçant des points ou des nœuds d'intersections d'éléments. Cependant, pour garantir que cette méthode crée le plus grand effet déstabilisant, plusieurs modèles avec divers scénarios devront être réalisés. Cela est assez chronophage et fastidieux.
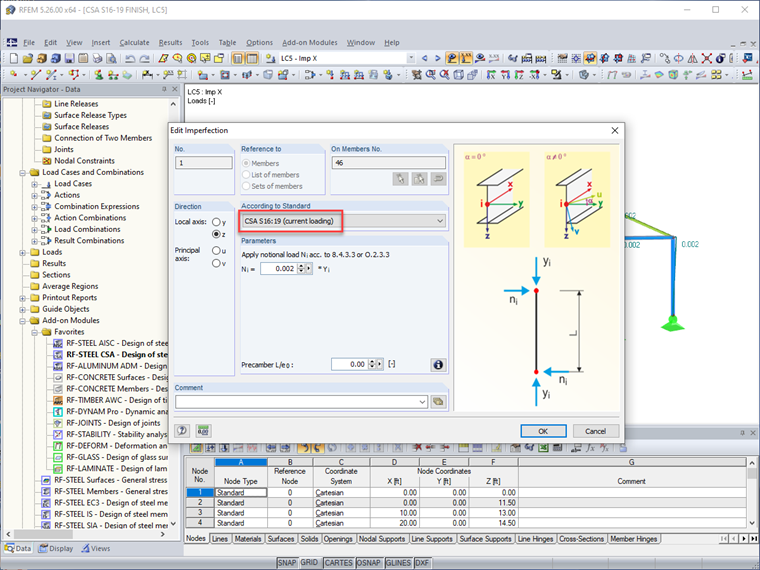
L'approche alternative est d'appliquer des charges notionnelles avec les options d'imperfections dans RFEM. Cette boîte de dialogue inclut maintenant la CSA S16:19 dans les options déroulantes. La charge notionnelle est appliquée à l'extrémité de l'élément (c'est-à-dire en haut de colonne) avec une amplitude égale à 0.002 (ou 0.005 si utilisant la méthode simplifiée de stabilité) multipliée par la force axiale de l'élément (charge gravitaire appliquée). Une force égale et opposée est appliquée en interne à l'extrémité opposée de l'élément pour éviter des cisaillements de base irréalistes de la structure.
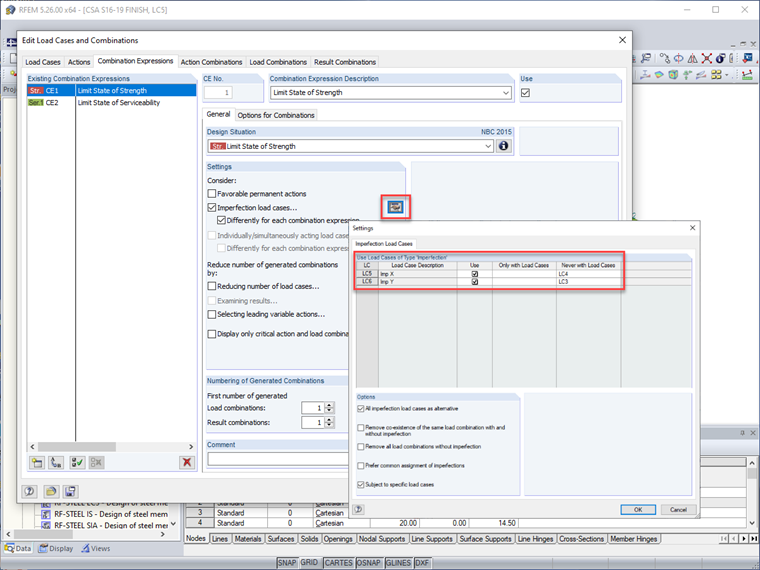
Ces cas de charge d'imperfection peuvent être appliqués dans RFEM avec des cas de charge latéraux spécifiques pour produire la plus grande action déstabilisante tout en évitant la génération de combinaisons de charges qui ne seront pas dirigeantes et qui augmenteront encore le temps de calcul (c'est-à-dire que les charges notionnelles dans la direction X ne doivent être appliquées qu'avec des charges de vent dans la direction X). De plus, les imperfections peuvent être complètement désactivées pour les expressions de combinaison de charges de service tout en étant toujours appliquées aux combinaisons de résistance.
Effets d'Inhomogénéité
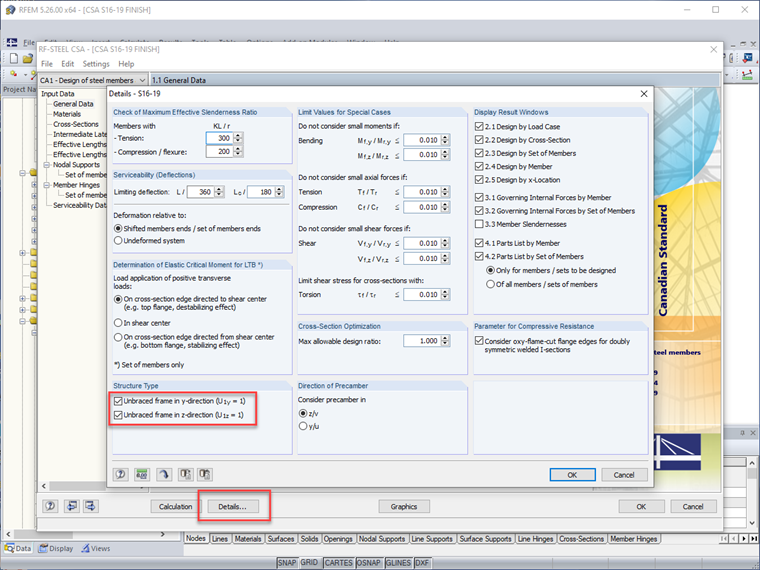
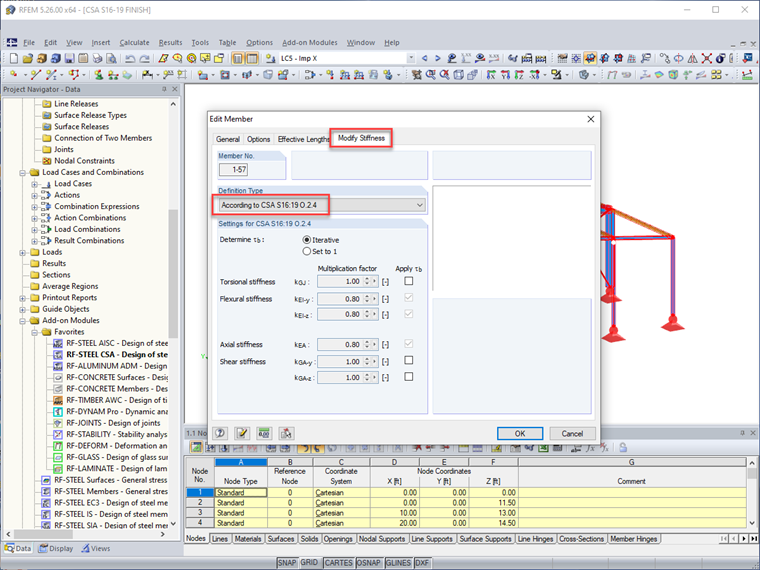
L'onglet de modification de la rigidité pour les membres inclut maintenant la norme CSA S16:19. Lorsque cette option est sélectionnée, le facteur de modification 0.8 et le facteur τb calculé sont appliqués directement à la rigidité en flexion et axiale du membre. Les utilisateurs ont également l'option d'appliquer davantage ces réductions à la rigidité à la torsion et en cisaillement de l'élément.
Parce que la réduction de rigidité des éléments ne doit pas être considérée pour la conception de service (c'est-à-dire, les déformations), RFEM permet aux utilisateurs de désactiver toutes les modifications de rigidité des éléments pour les combinaisons de charges de service tout en laissant ceci actif pour les combinaisons de charges de résistance.
Résumé
Des mises à jour significatives de la conception de la stabilité selon l'Annexe O.2 dans le dernier manuel de conception en acier canadien CSA S16:19 sont maintenant entièrement intégrées dans le flux de travail d'analyse RFEM. Ces mises à jour incluent de manière significative la capacité de considérer les charges notionnelles comme des imperfections, ainsi que des rigidités réduites pour les éléments selon la CSA S16:19. Pour voir ces nouvelles mises à jour démontrées dans une vidéo d'exemple détaillée, consultez le webinaire Conception en Acier CSA S16:19 dans RFEM.