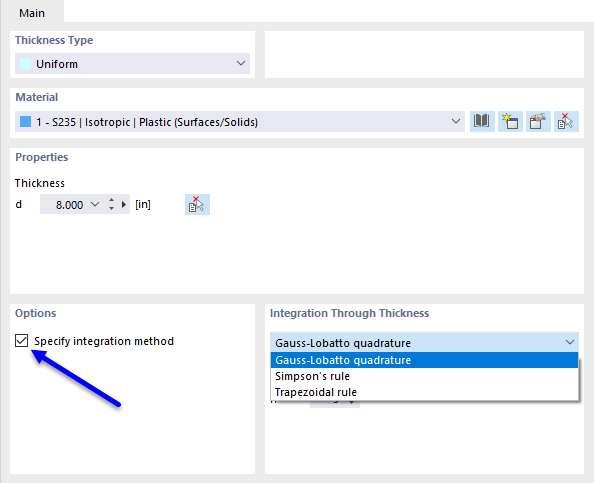
Как объясняется в технической статье "Пользовательский метод интеграции для определения внутренних сил в железобетонных плитах в программе RFEM 6", внутренние силы и моменты в плитах являются результатом численного интегрирования напряжений по толщине плиты (со статьей можно ознакомиться здесь) КБ 001817 ). В случае, когда используется нелинейный материал, в RFEM 6 можно выбрать между квадратурой Гаусса-Лобатто, правилом трапеций и правилом Симпсона. Кроме того, можно указать количество точек интегрирования от 3 до 99.
Теория методов интеграции объясняется в руководстве по многослойным поверхностям: Теория: Методы интеграции. Там же вы найдёте похожий пример трёхслойной плиты с точечным опиранием: Примеры расчета: Методы интеграции.
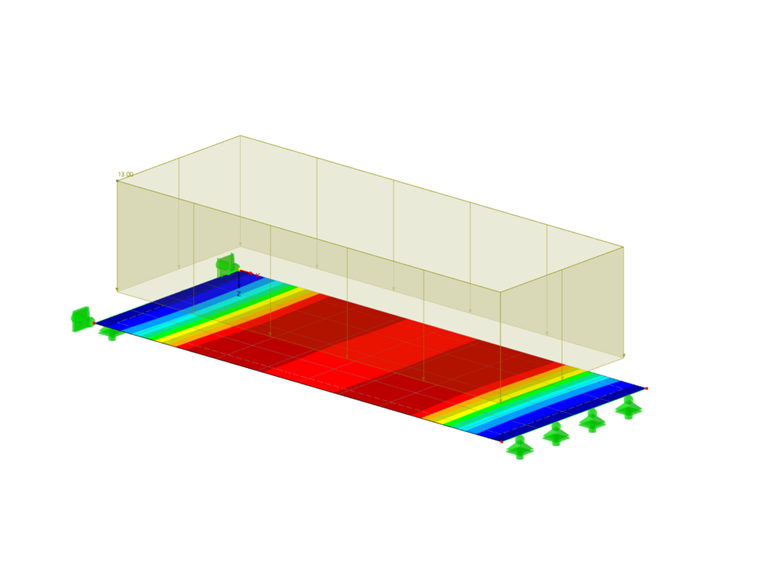
На этом примере, описывающем сталефибробетонную плиту, мы хотим показать, каким образом применением различных методов интегрирования и различного количества точек интегрирования влияет на результат расчета. Для этого возьмем плиту длиной 5 м, шириной 2 м и толщиной 30 см, для которой будет задана модель материала изотропного повреждения. Действующая нагрузка 13 кН/м², шаг сетки 0,5 м.
Метод интегрирования, а также количество точек интегрирования можно задать в основных данных для толщины плиты.
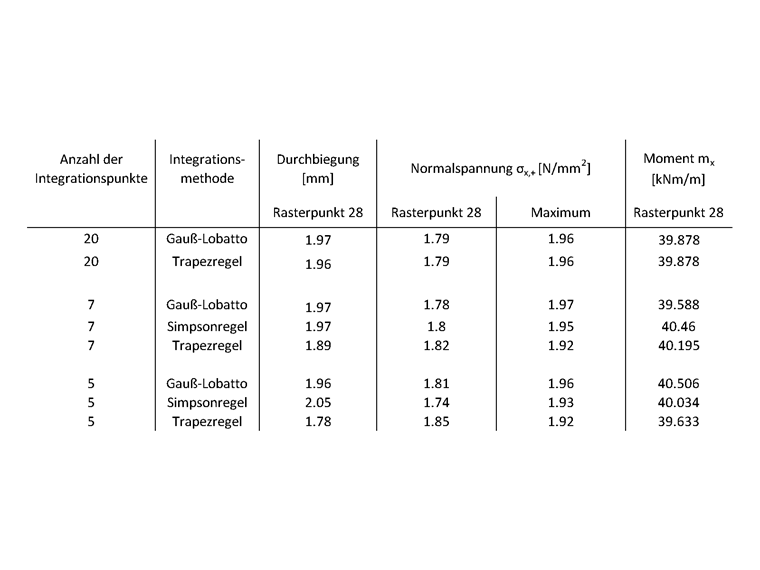
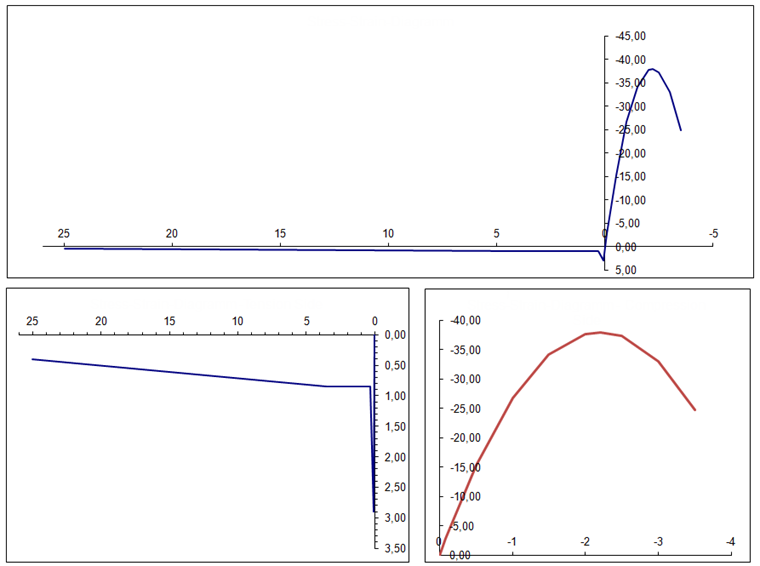
Расчет дает следующие результаты, в особенности учитывается центр пластины (точка решетки № 28).
При небольшом количестве точек интеграции возникают видимые различия между отдельными методами интегрирования. В частности, правило трапеций менее точно. Однако при более высоком количестве точек, результаты всех методов интегрирования приближаются к одному фиксированному решению. Квадратура Гаусса-Лобатто с девятью точками интегрирования, используемая по умолчанию в RFEM 6, достаточна в большинстве случаев. Однако, если к плите применяется очень высокая нагрузка, то различия между методами интеграции становятся еще более очевидными.
В частности, если ваш расчет достигает диапазона текучести сталефибробетона, то имеет смысл применить большее количество точек интегрирования, поскольку так можно лучше отобразить свойства материала. Параметры напряжения-деформации в этом диапазоне могут быть лишь неточно аппроксимированы с помощью полиномов, но именно на этом основаны численные методы интегрирования. Поэтому в данном случае имеет смысл применить правило трапеции или правило Симпсона, поскольку эти правила применяются к меньшей области и затем суммируются промежуточные результаты.
Свойства сталефибробетона объяснены в следующей технической статье: КБ | Определение характеристик сталефибробетона и его применение в программе RFEM