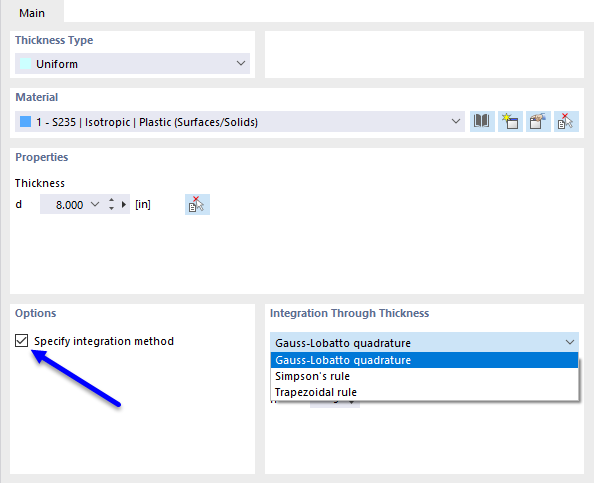
As explained in the technical article "User-Defined Integration Method for Determining Internal Forces in Slabs in RFEM 6", the internal forces and moments available in slabs result from the numerical integration of stresses occurring over the slab thickness (see KB 001817 ). If a nonlinear material is used, you can choose between the Gauss-Lobatto quadrature, the trapezoidal rule, and the Simpson's rule in RFEM 6. It is also possible to specify the number of integration points from 3 to 99.
The theory about the integration methods is described in the Multilayer Surfaces manual in the chapter Theory of Integration Methods. In this manual, you will also find a similar example for a point-supported three-layer slab under Calculation Examples: Integration Methods.
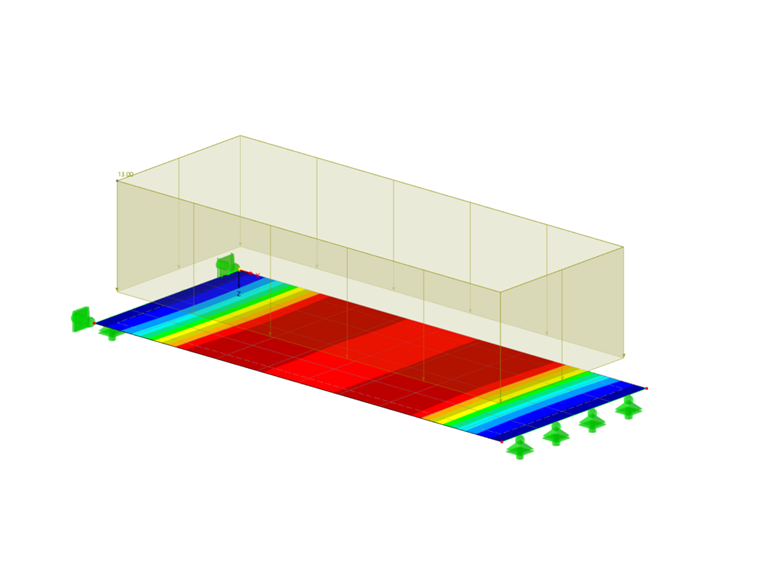
In this example describing a steel fiber-reinforced concrete slab, we want to show the effect concerning the difference of using several integration methods and of a different number of integration points on the calculation result. For this purpose, we consider a slab with a length of 5 m (about 16 ft), a width of 2 m (about 6 ft), and a thickness of 30 cm (almost 1 ft), for which the Isotropic Damage material model is used. A load of 13 kN/m² is applied and the mesh density is 0.5 m (1.6 ft).
The integration method as well as the number of integration points can be specified in the main data of the plate thickness.
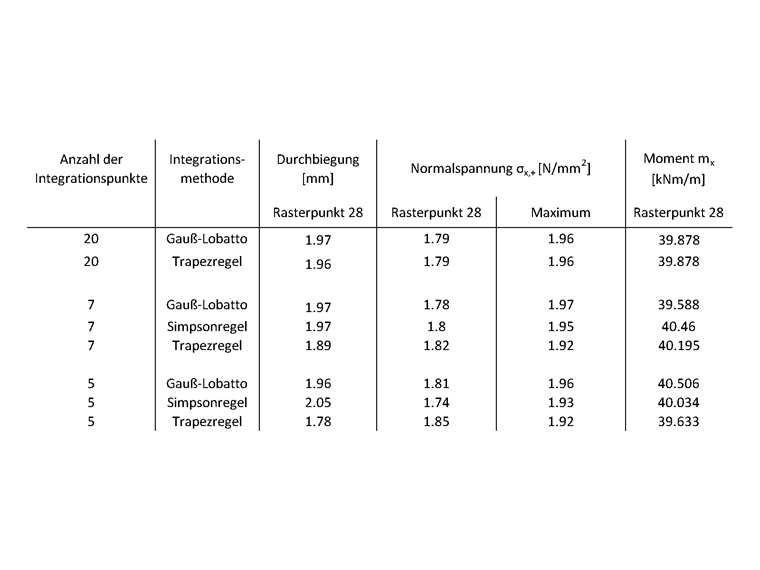
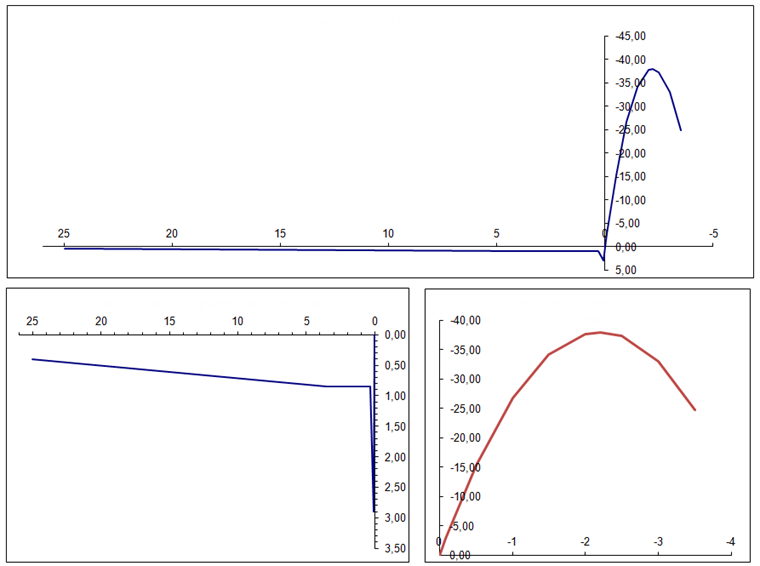
The calculation provides the following results, and the plate's center (grid point no. 28) is considered in particular.
For a small number of integration points, there are visible deviations among the individual integration methods. The trapezoidal rule, in particular, is less accurate. For a larger number, however, the results of all integration methods approach a fixed solution. The Gauss-Lobatto quadrature with nine integration points used by default in RFEM 6 is sufficient for most cases. However, if you apply a very high load on the slab, the differences between the integration methods become even more apparent.
In particular, if your calculation reaches into the steel fiber-reinforced concrete's yielding range, a higher number of integration points is useful, as the material behavior can be better represented in this way. The stress-strain behavior in this range can be approximated only imprecisely by polynomials, which is, however, what the numerical integration methods are based on. Therefore, it may be worth using the trapezoidal or the Simpson's rule in this case, since these rules are each applied to a smaller area and the partial results are added then.
The following technical article explains the material behavior of steel fiber-reinforced concrete: KB | Determining Material Properties of Steel Fiber-Reinforced Concrete and Their Application in RFEM