Как вы, возможно, уже знаете, RFEM 6 содержит возможности учета нелинейности материала. Из этой статьи вы узнаете, как определяются внутренние силы в плитах, смоделированных с использованием нелинейного материала.
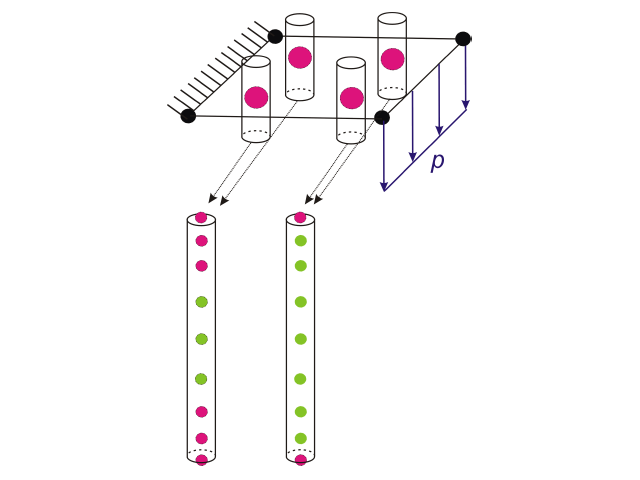
Внутренние силы в плитах с нелинейным материалом определяются с помощью численного интегрирования напряжений по толщине d пластины, как показано в формуле 1.
Обратите внимание на то, что числовая квадратура означает аппроксимацию вышеуказанного интеграла взвешенной конечной суммой (формула 2) для n точек по толщине -d/2 ≤ z1 <... n ≤ d/2, и так называемого веса wi, которые характерны для данной квадратуры и числа n.
До версии RFEM 6.02.0049 это численное интегрирование выполняется с помощью 9-точечного квадратурного правила Гаусса-Лобатто, содержащего конечные точки интервала, то есть верхнюю и нижнюю часть толщины. Это верно для полиномов до порядка 15 (2*9-3), независимо от модели материала или пользовательской диаграммы. На рисунке 1 показаны 9 узлов по толщине для квадратуры Гаусса-Лобатто в каждой плоскостной точке интегрирования в 2D конечном элементе.
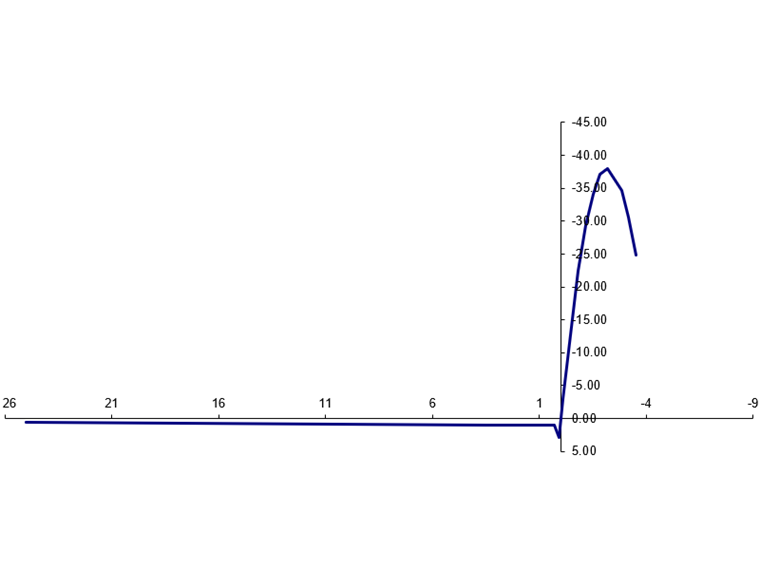
Следовательно, для материалов с «менее подходящей» кривой напряжение-деформация, внутренние силы в плите с сильными трещинами могут быть аппроксимированы стандартной схемой интегрирования с числовой ошибкой более 10%. Одним из таких материалов является фибробетон и его работа при растяжении. На рисунке 2 показана типичная диаграмма напряжения-деформации для фибробетона (растяжение слева, сжатие справа).
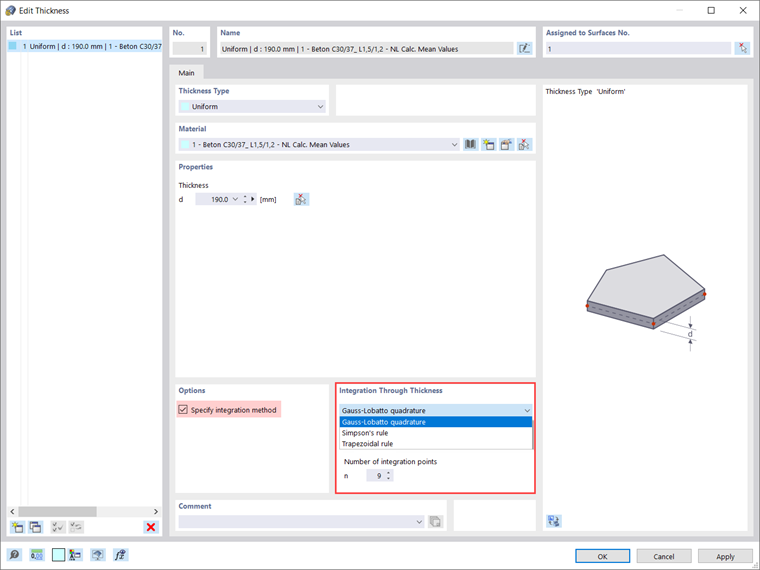
Для решения этой проблемы в RFEM 6.02.0049 введена пользовательская опция, с помощью которой можно задать подробности численного интегрирования по толщине плиты (рисунок 3). Эта опция позволяет пользователю изменять как количество точек интегрирования (от 3 до 99), так и само правило квадратуры. Теперь, кроме квадратуры Гаусса-Лобатто, вы можете выбрать правило трапеции или Симпсона. Однако учтите, что это, скорее всего, улучшит интеграцию только в некоторых исключительных случаях.
Также важно знать то, что правила Гаусса-Лобатто и Симпсона требуют нечетного количества точек интегрирования. Таким образом, если пользовательское число является четным, для расчета учитывается следующее по величине нечетное число. Другими словами, если пользовательский ввод, например, равен 4, в расчете используются 5 точек интегрирования по толщине.
Преимущество этой новой опции заключается в том, что вы можете повысить производительность вычислений за счет уменьшения количества точек интегрирования в 2D-элементах конструкции с нелинейными материалами. Например, вы можете уменьшить количество точек интегрирования в областях, которые не представляют большого интереса (например, в областях в упругом диапазоне).
Наиболее актуальным вопросом является «правильное» количество точек интегрирования. До сих пор, это вопрос, на который нет правильного ответа. Это зависит от диаграммы напряжения-деформации материала и фактического напряженного состояния конечных элементов при заданной нагрузке; поэтому в любом случае требуется помощь инженера.