538x
15x
Jak bylo vysvětleno v odborném článku Uživatelsky zadaná integrační metoda pro stanovení vnitřních sil v betonových deskách v programu RFEM 6, vnitřní síly a momenty v deskách vyplývají z numerické integrace napětí přes tloušťku desky (článek najdete zde). KB 001817 ). Pokud je použit nelineární materiál, můžete v programu RFEM 6 volit mezi Gauss-Lobattovou kvadraturou, lichoběžníkovým pravidlem a Simpsonovým pravidlem. Kromě toho je možné nastavit vlastní počet integračních bodů od 3 do 99.
Die Theorie zu den Integrationsmethoden wird im Handbuch zu mehrschichtigen Flächen erklärt: Theorie integračních metod. Dort finden Sie auch ein ähnliches Beispiel für eine dreischichtige, punktgestützte Platte: Příklady výpočtu: Integrační metody.
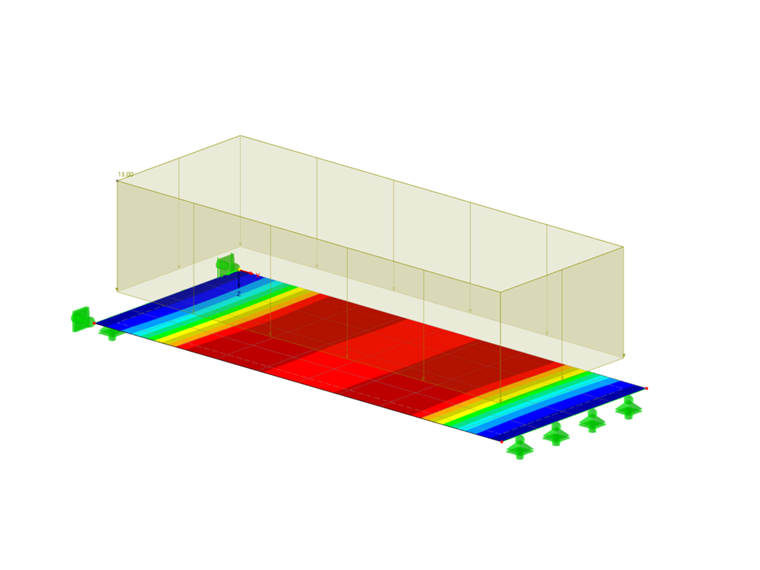
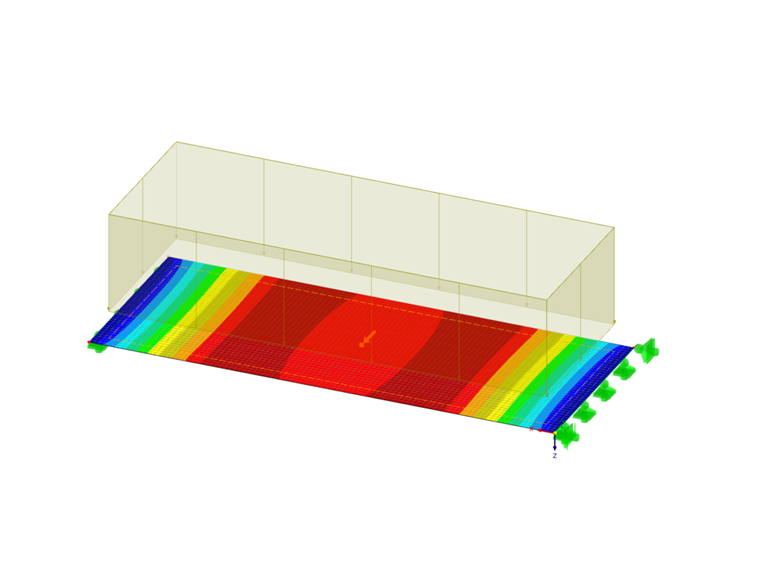
V tomto příkladu je předvedeno, jaký rozdíl ve výsledku výpočtu způsobí použití různých integračních metod a různého počtu integračních bodů pro desku z drátkobetonu. Pro tento účel se uvažuje 5 m dlouhá, 2 m široká a 30 cm silná deska s materiálovým modelem izotropní poškození. Působí na ni zatížení 13 kN/m² a velikost sítě je 0,5 m.
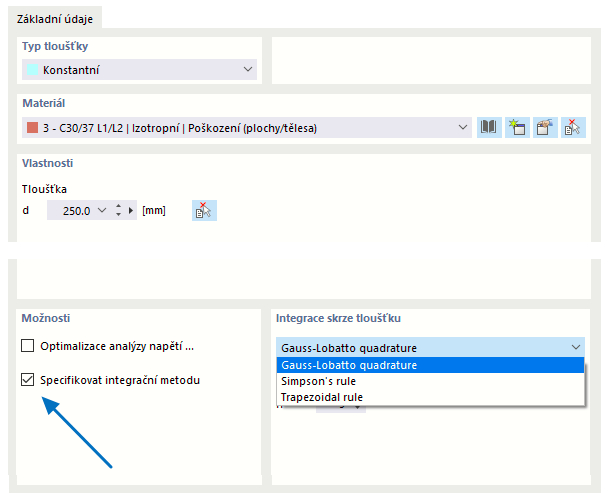
Metoda integrace a počet integračních bodů lze zadat v Základních údajích pro tloušťku desky.
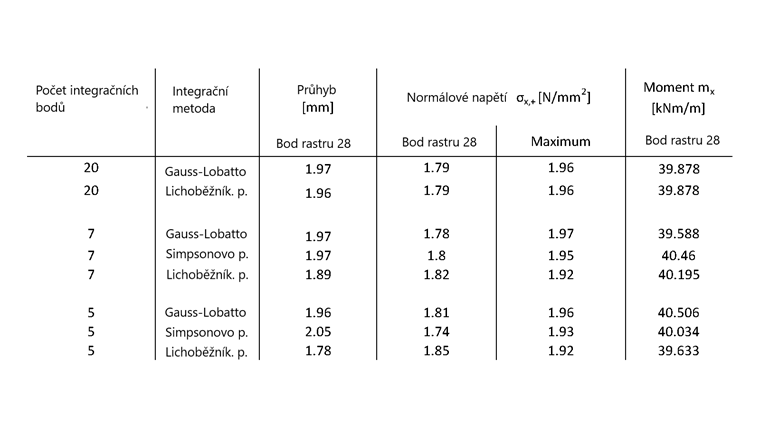
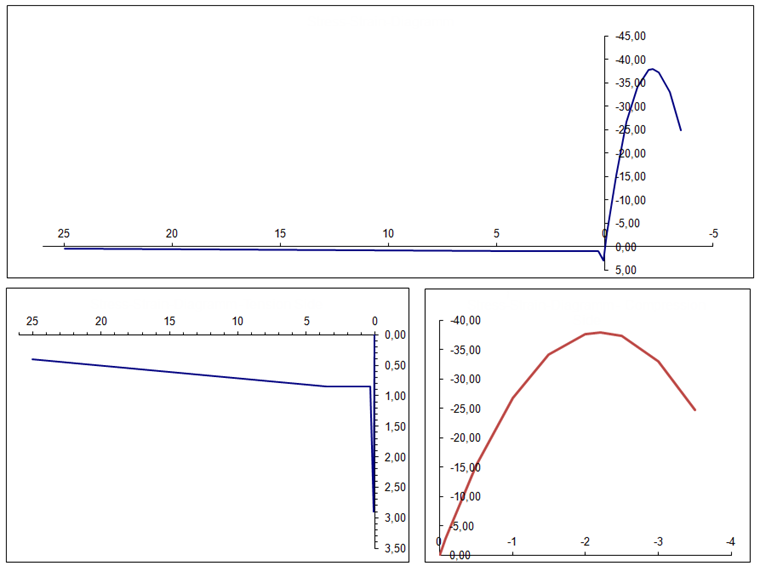
Výpočet poskytuje následující výsledky, přičemž se věnuje pozornost zejména středu desky (bod rastru č. 28).
Pro malý počet integračních bodů jsou mezi jednotlivými integračními metodami viditelné odchylky. Méně přesné je zejména lichoběžníkové pravidlo. S vyšším počtem bodů se však výsledky všech integračních metod blíží stejnému řešení. Pro většinu případů postačuje v programu RFEM 6 přednastavená Gaussova-Lobattova kvadratura s 9 integračními body. Pokud však desku zatížíte velmi vysokým zatížením, rozdíly mezi integračními metodami se zvýrazní.
Zejména při výpočtu v oblasti kluzu drátkobetonu je smysluplný vyšší počet integračních bodů, protože tak lze lépe modelovat chování materiálu. Deformační chování v této oblasti lze jen stěží aproximovat polynomy, na čemž je numerická integrace založena. Proto může být užitečné v tomto případě použít lichoběžníkové pravidlo nebo Simpsonovo pravidlo, protože ta se aplikují vždy na menší oblast a dílčí výsledky se pak sečtou.
In diesem Fachbeitrag ist das Materialverhalten von Stahlfaserbeton erklärt: Stanovení materiálových vlastností drátkobetonu a jeho použití v programu RFEM
![Rozpětí podle obr. 5.2 z [1]](/cs/webimage/039540/3493372/01_Abmessungen_EN.png?mw=512&hash=3cc425f1463bd5981b358d5889e3109e07ae1233)
.JPG?mw=350&hash=354dcaeb798219977d00c1979f12a0628654c9f0)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)