562x
22x
Comme expliqué dans l'article technique Méthode d'intégration définie par l'utilisateur pour la détermination des efforts internes dans les dalles en béton de RFEM 6, les efforts internes et les moments dans les dalles résultent de l'intégration numérique des contraintes sur l'épaisseur de la dalle (vous pouvez trouver l'article ici). KB 001817 ). Si un matériau non linéaire est utilisé, vous pouvez choisir entre la quadrature de Gauss-Lobatto, la méthode des trapèzes et la méthode de Simpson dans RFEM 6. Il est également possible de définir vous-même le nombre de points d'intégration de 3 à 99.
Die Theorie zu den Integrationsmethoden wird im Handbuch zu mehrschichtigen Flächen erklärt: Théorie : Méthodes d'intégration. Dort finden Sie auch ein ähnliches Beispiel für eine dreischichtige, punktgestützte Platte: Exemples de calcul : Méthodes d'intégration.
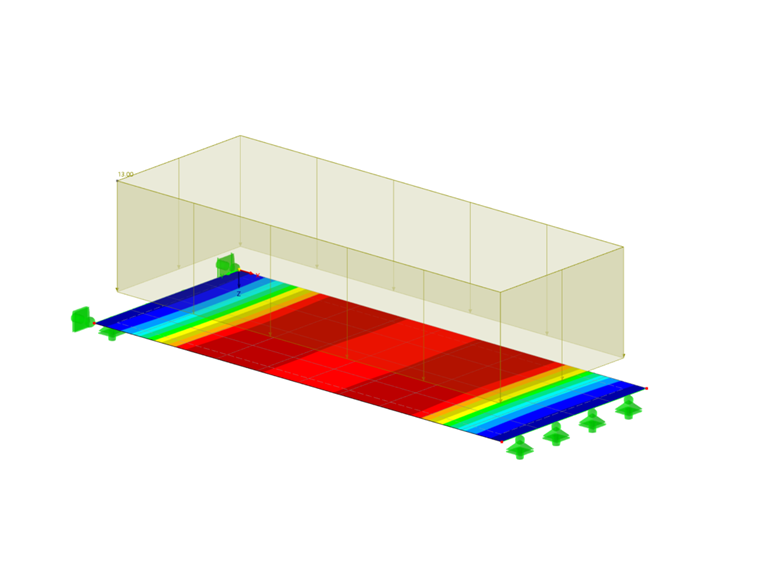
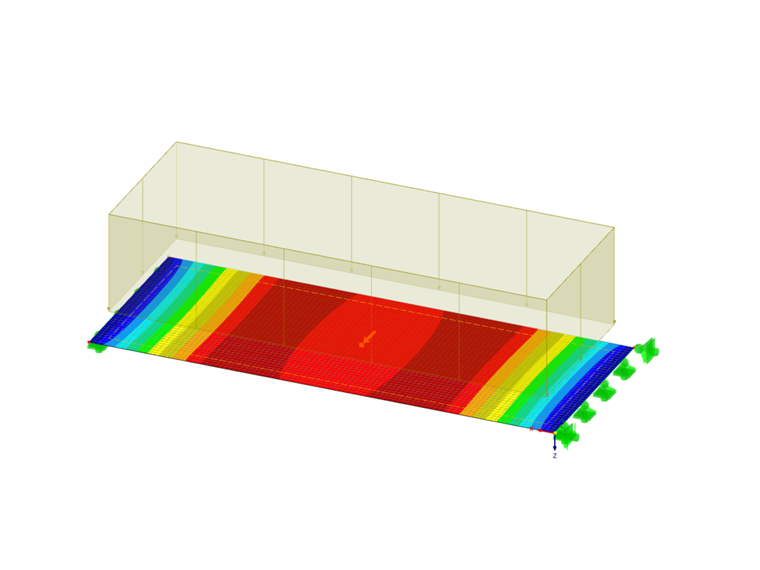
Dans cet exemple, nous voulons montrer quelle différence l'utilisation des différentes méthodes d'intégration et un nombre différent de points d'intégration ont sur le résultat du calcul dans le cas d'une dalle en béton fibré. Pour ce faire, une plaque de 5 m de long, 2 m de large et 30 cm d'épaisseur est considérée, pour laquelle le modèle de matériau d'endommagement isotrope est utilisé. Une charge de 13 kN/m² est appliquée et la densité du maillage est de 0,5 m.
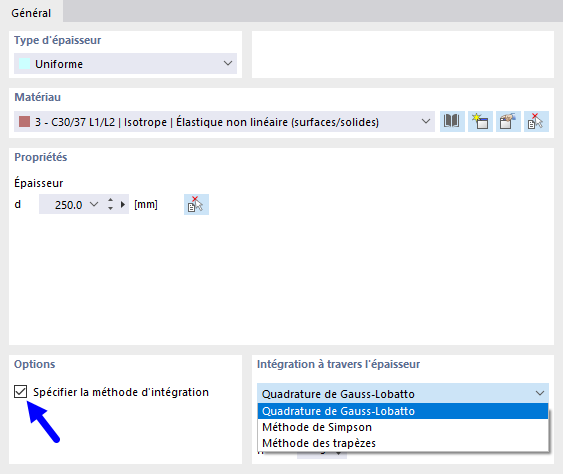
La méthode d'intégration ainsi que le nombre de points d'intégration peuvent être spécifiés dans les données générales de l'épaisseur de la dalle.
Le calcul donne les résultats suivants, le centre de la plaque (point de grille n° 28) étant considéré en particulier.
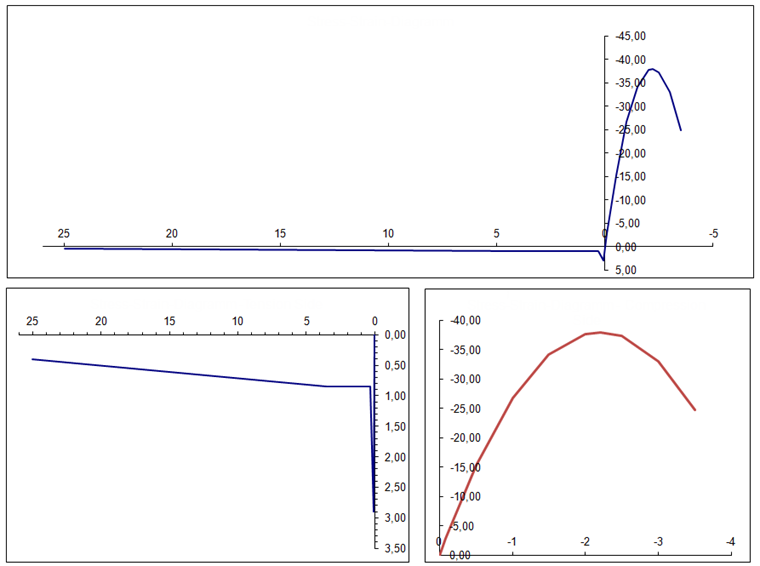
Pour un petit nombre de points d'intégration, il existe des écarts visibles entre les différentes méthodes d'intégration. La méthode des trapèzes en particulier est moins précise. Cependant, avec un nombre plus élevé, les résultats de toutes les méthodes d'intégration se rapprochent d'une solution fixe. La quadrature de Gauss-Lobatto avec 9 points d'intégration utilisée par défaut dans RFEM 6 est suffisante dans la plupart des cas. Cependant, si vous placez une charge très élevée sur la plaque, les différences entre les méthodes d'intégration deviennent encore plus apparentes.
Un nombre de points d'intégration plus élevé est particulièrement utile si vous calculez jusqu'à la plastification du béton fibré, car le comportement du matériau peut ainsi être mieux représenté. La courbe contrainte-déformation dans cette zone peut difficilement être estimée par des polynômes, mais les méthodes numériques d'intégration sont basées sur cela. Par conséquent, il peut être intéressant d'utiliser la méthode des trapèzes ou la méthode de Simpson dans ce cas, car elles sont chacune appliquées à une zone plus petite et les résultats partiels sont ensuite ajoutés.
In diesem Fachbeitrag ist das Materialverhalten von Stahlfaserbeton erklärt: ko | Détermination des propriétés de matériau du béton fibré et son utilisation dans RFEM