描述
现有标准如 EN 1991-1-4 [1],ASCE/SEI 7-16 和 NBC 2015 提供了风荷载参数,包括基本结构形状的风压系数 (Cp)。然而,关键的挑战在于如何更高效、准确地确定这些参数,而不是依赖标准中通常费时且复杂的公式化方法。
CFD 模拟的关键方面之一是选择准确且兼容的配置,如湍流模型、风速剖面、湍流强度、边界层条件和离散化顺序。然而,EN 1991-1-4 中没有明确指出这些数值细节。
在当前涉及柱体结构的验证示例中,我们提出了一组与欧码框架相一致的推荐 CFD 设置。如 EN 1991-1-4 所述,Cp 值的确定基于随雷诺数变化的复杂公式,可以通过良好校准的 CFD 方法进行简化。
分析解答
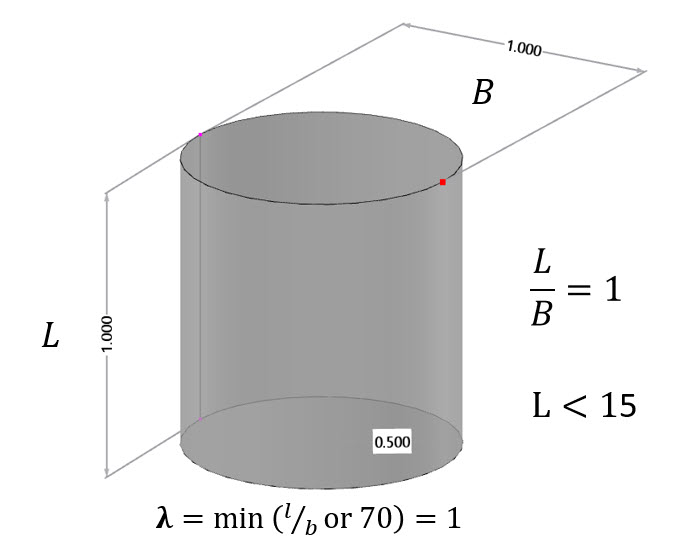
如图 1 所示,柱体的尺寸设计是为了根据 EN 1991-1-4 的公式 7.15 达到 Re= 2*106 的雷诺数。在这个公式中,b 代表柱体直径,ν 是空气的运动粘性系数 (ν=15*10-6 m2/s),而 v(ze) 表示参考高度 ze 处的最大风速:
以下是假设和推荐设置(表 1),其与欧码示例中的 Cp 和力系数值较为一致:
| 风速 | V | 30 | 米/秒 |
| 雷诺数 (公式 7.15, EN 1991-1-4) | Re | 2*106 | - |
| 高度 | L | 1 | 米 |
| 直径 | D | 1 | 米 |
| 最小压力/流动分离位置 (表 7.12, EN 1991-1-4) | αmin/αA | 80/120 | 度 |
| 最小压力系数值 (表 7.12, EN 1991-1-4) | Cp0,min | -1.9 | - |
| 基础压力系数 (表 7.12, EN 1991-1-4) | Cp0,h | -0.7 | - |
| 密度比 (公式 7.28, EN 1991-1-4) | φ | 1 | - |
| 有效细长比 (表 7.16, EN 1991-1-4) | λ | 1 | - |
| 端部效应因子 (图 7.36 - 公式 7.17, EN 1991-1-4) | ψλ - ψλa | 0.6-(0.6-1) | - |
| 力系数 (图 7.28, EN 1991-1-4) | Cf,0 | 0.55 | - |
| 空气密度 | ρ | 1.25 | 千克/立方米 |
| 湍流模型 | 稳态 RANS k-ω SST | - | - |
| 运动粘性系数 (公式 7.15, EN 1991-1-4) | ν | 1.5*10-5 | 平方米/秒 |
| 方案顺序 | 二阶 | - | - |
| 残差目标值 | 10-5 | - | - |
| 残差类型 | 压力 | - | - |
| 最小迭代次数 | 800 | - | - |
| 边界层 | NL | 10 | - |
| 墙面函数类型 | 增强 / 混合 | - | - |
| 湍流强度 (最佳拟合) | I | 7.5%-15% | - |
结果
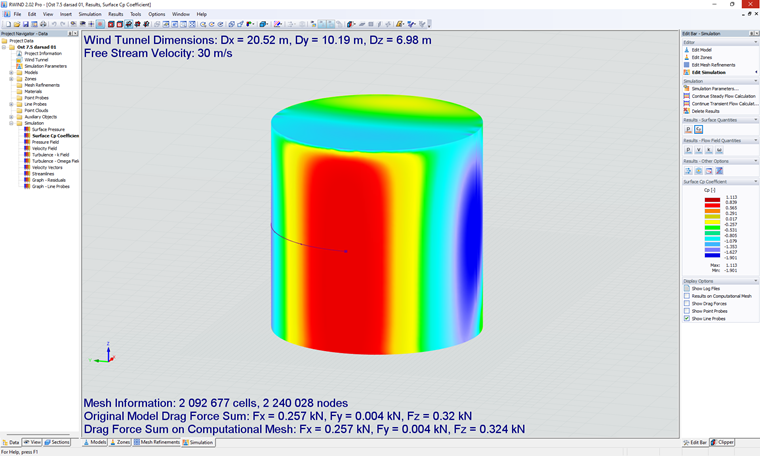
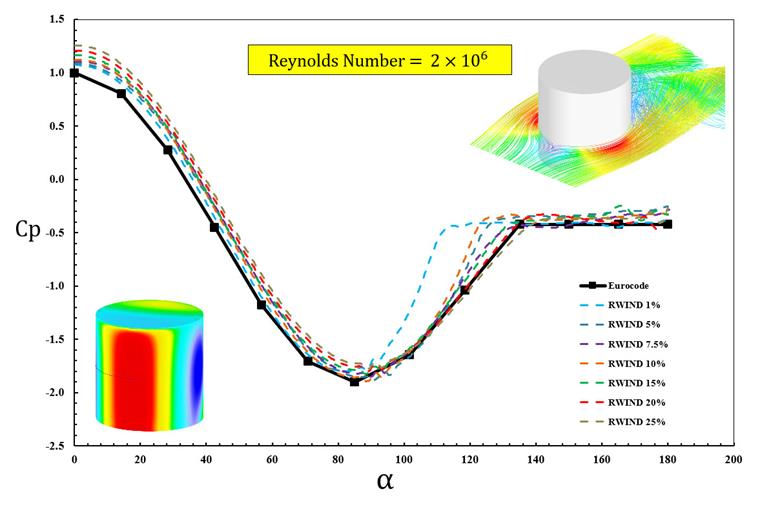
最后,对于 7.5% 的湍流强度的 Cp 等高线 (图 2) 和不同湍流强度的图表绘制在图 3 中,其中 I=7.5% 在预测平均风压系数方面显示出更好的一致性。对于另一个标准 (表 2 中的力系数 Cf,0),根据 EN 1991-1-4 的图 7.28,其 15% 的数值更接近日常法典示例。
| 湍流强度 (%) | Fd (N) | ρ (千克/立方米) | u (米/秒) | A (平方米) | Cf,0 |
| 1.00 | 253 | 1.25 | 30 | 1 | 0.45 |
| 5.00 | 226 | 1.25 | 30 | 1 | 0.40 |
| 7.50 | 253 | 1.25 | 30 | 1 | 0.46 |
| 10.00 | 257 | 1.25 | 30 | 1 | 0.46 |
| 15.00 | 303 | 1.25 | 30 | 1 | 0.54 |
| 20.00 | 328 | 1.25 | 30 | 1 | 0.58 |
| 25.00 | 361 | 1.25 | 30 | 1 | 0.64 |
| 欧码 | - | - | - | - | 0.55 |
同时,带有推荐设置的柱体模型可以从这里下载: