Opis
Istniejące normy, takie jak EN 1991-1-4 [1], ASCE/SEI 7-16 i NBC 2015, dostarczają parametry obciążenia wiatrem, w tym współczynnik ciśnienia wiatru (Cp), dla podstawowych kształtów konstrukcyjnych. Jednak kluczowym wyzwaniem jest określenie tych parametrów w bardziej efektywny i dokładny sposób, zamiast polegania na czasochłonnych i często złożonych podejściach bazujących na formułach znalezionych w normach.
Jednym z kluczowych aspektów symulacji CFD jest wybór dokładnych i kompatybilnych konfiguracji, takich jak model turbulencji, profil prędkości wiatru, intensywność turbulencji, warunki warstwy granicznej i kolejność dyskretyzacji. Jednak te szczegóły numeryczne nie są wyraźnie określone w EN 1991-1-4.
W obecnym przykładzie walidacji dotyczącej struktury cylindra proponujemy zestaw zalecanych ustawień CFD, które są zgodne z ramami Eurokodu. Jak określono w EN 1991-1-4, określenie wartości Cp opiera się na złożonych formułach, które zmieniają się wraz z liczbą Reynoldsa, co można uprościć poprzez dobrze skalibrowane podejścia CFD.
Rozwiązanie Analityczne
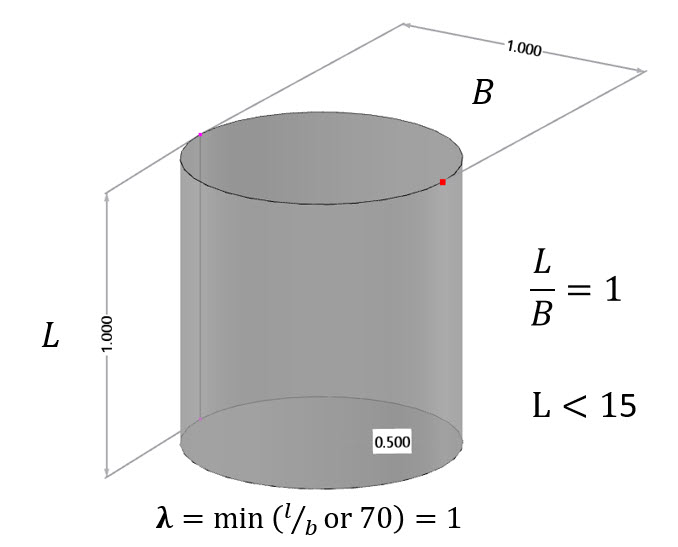
Wymiary cylindra, jak pokazano na Rysunku 1, są zaprojektowane w celu osiągnięcia liczby Reynoldsa Re= 2*106 na podstawie Równania 7.15 z EN 1991-1-4. W tym równaniu, b oznacza średnicę cylindra, ν to lepkość kinematyczna powietrza (ν=15*10-6 m2/s), a v(ze) denotuje szczytową prędkość wiatru na wysokości odniesienia ze:
Założenia i zalecane ustawienia CFD, podsumowane w Tabeli 1, wykazują poprawioną zgodność z wartościami współczynnika ciśnienia Cp i współczynnika siły podanymi w przykładzie Eurokodu:
| Prędkość Wiatru | V | 30 | m/s |
| Liczba Reynoldsa (Równanie 7.15, EN 1991-1-4) | Re | 2*106 | - |
| Wysokość | L | 1 | m |
| Średnica | D | 1 | m |
| Pozycja Minimalnego Ciśnienia/Separacji Przepływu (Tabela 7.12, EN 1991-1-4) | αmin/αA | 80/120 | Stopień |
| Wartość Minimalnego Współczynnika Ciśnienia (Tabela 7.12, EN 1991-1-4) | Cp0,min | -1.9 | - |
| Współczynnik Ciśnienia Podstawy (Tabela 7.12, EN 1991-1-4) | Cp0,h | -0.7 | - |
| Współczynnik Wzajemnego Zacienienia (Równanie 7.28, EN 1991-1-4) | φ | 1 | - |
| Skuteczna Smukłość (Tabela 7.16, EN 1991-1-4) | λ | 1 | - |
| Współczynnik Końca Efektu (Rysunek 7.36 - Równanie 7.17, EN 1991-1-4) | ψλ - ψλa | 0.6-(0.6-1) | - |
| Współczynnik Siły (Rysunek 7.28, EN 1991-1-4) | Cf,0 | 0.55 | - |
| Gęstość Powietrza | ρ | 1.25 | kg/m3 |
| Model Turbulencji | Steady RANS k-ω SST | - | - |
| Lepkość Kinematyczna (Równanie 7.15, EN 1991-1-4) | ν | 1.5*10-5 | m2/s |
| Kolejność Schemat | Druga | - | - |
| Wartość Docelowa Reszty | 10-5 | - | - |
| Typ Reszty | Ciśnienie | - | - |
| Minimalna Liczba Iteracji | 800 | - | - |
| Warstwa Graniczna | NL | 10 | - |
| Typ Funkcji Ściany | Enhanced / Blended | - | - |
| Intensywność Turbulencji (Dopasowanie Najlepsze) | I | 7.5%-15% | - |
Wyniki
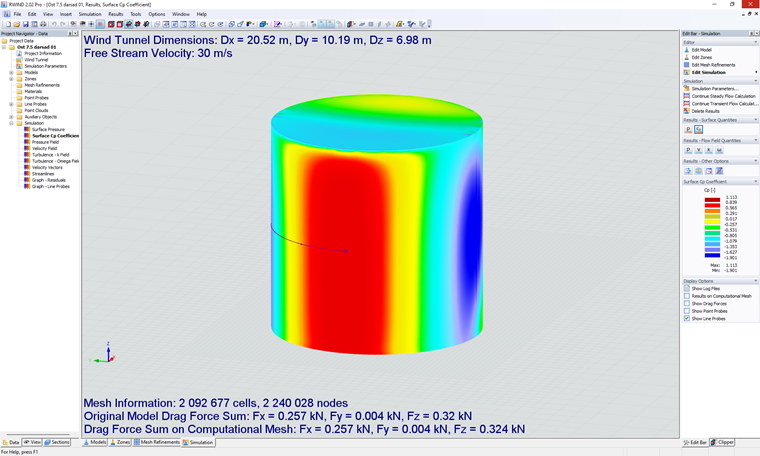
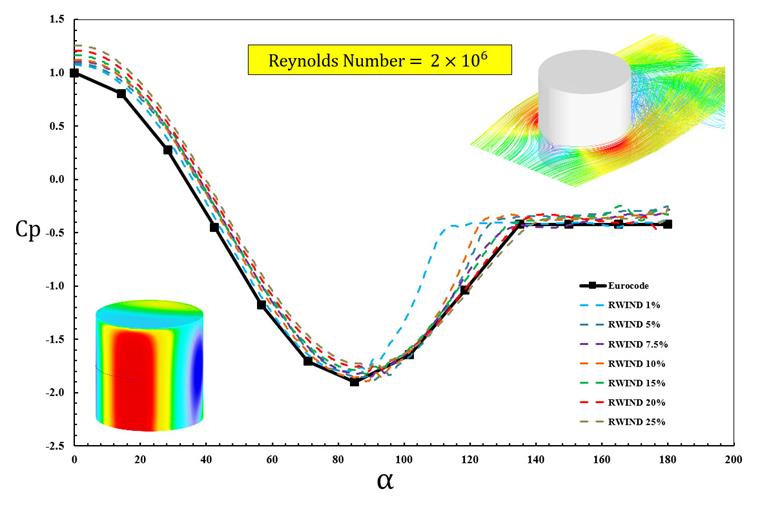
Na koniec przedstawiono kontur Cp dla intensywności turbulencji 7.5% na Rysunku 2, a odpowiadający diagram dla różnych intensywności turbulencji jest przedstawiony na Rysunku 3. Wśród testowanych przypadków intensywność turbulencji I=7.5% wykazuje najlepszą zgodność w przewidywaniu średniego współczynnika ciśnienia wiatru.
Jednakże, biorąc pod uwagę inny kluczowy parametr, mianowicie współczynnik siły Cf,0 (jak wymieniono w Tabeli 2 i odniesione na Rysunku 7.28 z EN 1991-1-4), intensywność turbulencji 15% daje wyniki bardziej zgodne z przykładem Eurokodu.
| Intensywność Turbulencji (%) | Fd (N) | ρ (kg/m3) | u (m/s) | A (m2) | Cf,0 |
| 1.00 | 253 | 1.25 | 30 | 1 | 0.45 |
| 5.00 | 226 | 1.25 | 30 | 1 | 0.40 |
| 7.50 | 253 | 1.25 | 30 | 1 | 0.46 |
| 10.00 | 257 | 1.25 | 30 | 1 | 0.46 |
| 15.00 | 303 | 1.25 | 30 | 1 | 0.54 |
| 20.00 | 328 | 1.25 | 30 | 1 | 0.58 |
| 25.00 | 361 | 1.25 | 30 | 1 | 0.64 |
| Eurokod | - | - | - | - | 0.55 |
Dodatkowo, model cylindra z zalecanymi ustawieniami CFD jest dostępny do pobrania tutaj: