Generalidades
O módulo adicional RF-/CONCRETE Columns dimensiona elementos de compressão em betão armado através do método da curvatura nominal descrito no Eurocódigo 2, Capítulo 5.8.8. Noutras normas este método é designado de método do pilar modelo. Num artigo anterior é descrito em detalhe a determinação das excentricidades de carga que tem de ser aplicadas quando é utilizado o método da curvatura nominal. Por esse motivo, a determinação das excentricidades individuais não será descrita detalhadamente aqui.
Dimensionamento separado na direção do eixo principal sem consideração da interação de momento biaxial
De acordo com 5.8.9 (2), EN 1992-1-1 [1], é permitido dimensionar separadamente um pilar com excentricidade de carga biaxial nas duas direções principais, sem ter em consideração a interação do momento, se os limites segundo as Equações 5.38a e 5.38b [1] forem cumpridos. As descrições das equações podem ser encontradas no artigo mencionado anteriormente. Esses limites e a abordagem de dimensionamento são baseados no facto de que uma das duas excentricidades de carga representa o valor dominante e a segunda representa o valor subordinado.
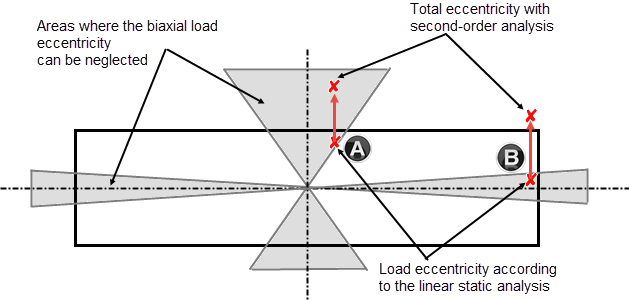
Ao dimensionar separadamente as direções dos eixos principais, a excentricidade adicional da imperfeição tem de ser considerada apenas na direção dominante, ou seja, na direção determinante. A Figura 01 mostra quais áreas não precisam de ser consideradas para a flexão biaxial. Se a força axial excêntrica se encontra nas áreas sombreadas, o pilar pode ser dimensionado separadamente nas duas direções principais. É necessário ter em atenção que as excentricidades de carga têm de ser consideradas de acordo com a análise de segunda ordem nas respetivas direções principais.
Isto também é apresentado na Figura 01. Os pontos A e B na Figura 01 simbolizam dois exemplos de uma possível posição de carga onde a influência da excentricidade de acordo com a análise de segunda ordem tem efeitos diferentes. Sem considerar a análise de segunda ordem (e2), os dois pontos estão localizados em áreas sombreadas e permitidas, onde o dimensionamento da flexão biaxial pode ser desprezado. Ao considerar a excentricidade de acordo com a análise de segunda ordem, a excentricidade da carga biaxial é reduzida para o ponto A, enquanto para a posição de carga B, a flexão biaxial é aumentada e a carga é deslocada para fora do intervalo permitido.
Dimensionamento separado na direção do eixo principal considerando a interação de momento biaxial
Se as condições da Equação 5.38a e Equação 5.38b [1] não são cumpridas, os pré-requisitos para o dimensionamento separado na direção do eixo principal sem considerar a interação do momento biaxial de acordo com 5.8.9 (2) não estão dados. A seção (4) do capítulo 5.8.9 [1] utiliza a Equação 5.39 para descrever uma abordagem simplificada que pode ser usada para considerar a interação do momento biaxial com o dimensionamento anterior das direções dos eixos principais individuais.
A seguinte Equação 5.39 [1] considera a interação de momento de uma forma simplificada.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
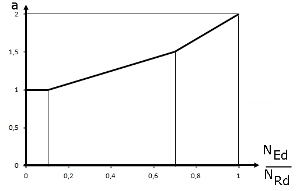
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
A Figura 02 mostra o expoente a em função da relação NEd/NRd. NRd é o valor de cálculo da resistência axial central e pode ser determinado com NRd = Ac ⋅ fcd + As + fyd. Ac representa a secção transversal de área bruta, As representa a área de armadura longitudinal e fcd ou fyd representa as resistências de cálculo dos materiais utilizados.
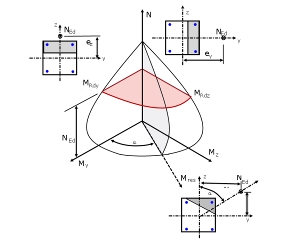
Ao utilizar a Equação 5.39 [1], é necessário ter em conta que as duas resistências de flexão MRdy e MRdz têm de ser tomadas a partir dos diagramas de interação de cálculo para as duas direções principais quando se tem uma força axial constante (ver Figura 03).
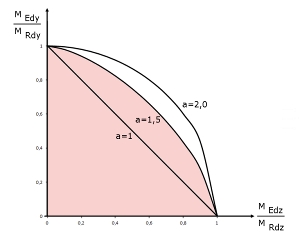
Na Figura 03 é representado um quadrante de um diagrama de interação tridimensional My-Mz-N. A Equação 5,39 baseia-se na simplificação de uma secção horizontal em NEd usando o diagrama de interação 3D e gerando um diagrama de interação de momentos My-Mz através do expoente a. Na Figura 03, o diagrama de interação atual do momento My-Mz para a força axial NEd (corte horizontal) está representado sombreado a vermelho. O diagrama de interação simplificado de acordo com a Equação 5.39 também está sombreado a vermelho, para poder ser comparado. A Figura 04 mostra, dependendo do expoente a, o diagrama da interação de momentos aplicado na Equação 5.39 [1].
A vantagem desta abordagem simplificada de acordo com a Equação 5.39 [1] é que os elementos de compressão com excentricidades biaxiais também podem ser dimensionados de forma rápida e fácil por meio dos diagramas de interação M-N conhecidos para flexão simples com força axial.
Dimensionamento exato da secção de secção com excentricidade de carga biaxial
Um dimensionamento preciso de uma seção transversal com força axial e flexão biaxial requer um cálculo iterativo das deformações da secção. O cálculo destas deformações de secção só é possível com uma ferramenta de cálculo. A verificação do estado limite último é cumprida quando a carga se encontra dentro do diagrama de interação Mres–N (área sombreada a cinzento na Figura 03) ou no diagrama de momentos Mz-My determinado com exatidão (área sombreada a vermelho na Figura 03). Através da determinação com precisão das curvas de limite, podem ser geradas capacidades de carga adicionais para o dimensionamento.
Conclusão
Para uma excentricidade de carga biaxial, a norma permite diferentes métodos de dimensionamento, dependendo da posição de carga. Respeitando as condições de fronteira das Equações 5.38a e 5.38b [1], a interação biaxial de momentos pode ser desprezada e o dimensionamento pode ser realizado nas direções dos eixos principais. Se os limites mencionados acima forem excedidos, a interação de momentos tem de ser considerada no dimensionamento. Isto é possível de forma simplificada com a fórmula de interação de acordo com a Equação 5.39 [1] ou através de uma análise biaxial precisa da secção. Todas as abordagens de dimensionamento descritas são possíveis com o módulo adicional RF-/CONCRETE Columns.