Generale
Il modulo aggiuntivo RF-/CONCRETE Columns progetta elementi compressi in cemento armato con il metodo della curvatura nominale come descritto nell'Eurocodice 2, paragrafo 5.8.8. Altre norme descrivono questo metodo come il metodo della colonna del modello. Un articolo precedente descrive in dettaglio la determinazione delle eccentricità del carico che devono essere applicate quando si utilizza il metodo della curvatura nominale. Per questo motivo, la determinazione delle singole eccentricità non sarà descritta in dettaglio qui.
Verifica separata nella direzione dell'asse principale senza considerare l'interazione del momento biassiale
Secondo 5.8.9 (2), EN 1992-1-1 [1], è consentito progettare una colonna con eccentricità del carico biassiale separatamente in entrambe le direzioni dell'asse principale senza tener conto l'interazione del momento, se i limiti delle equazioni 5.38a e 5.38b [1] sono soddisfatti. Le equazioni sono descritte nell'articolo collegato sopra. Questi limiti e l'approccio progettuale si basano sul fatto che una delle due eccentricità del carico rappresenta il valore dominante e la seconda rappresenta il valore subordinato.
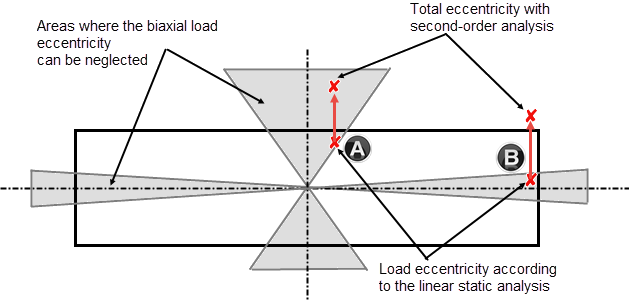
Quando si progetta nelle direzioni separate dell'asse principale, l'eccentricità aggiuntiva dall'imperfezione deve essere considerata solo nella direzione dominante, il che significa nella direzione determinante. La figura 01 mostra quali aree non devono essere considerate per la flessione biassiale. Se la forza assiale eccentrica si trova nelle aree ombreggiate, è possibile progettare la colonna separatamente in entrambe le direzioni principali. Si noti che le eccentricità del carico devono essere considerate secondo l'analisi del secondo ordine nelle rispettive direzioni dell'asse principale.
Questo è anche mostrato nella figura 01. I punti A e B nella figura 01 rappresentano due esempi di una possibile posizione di carico in cui l'influenza dell'eccentricità secondo l'analisi del secondo ordine ha effetti diversi. Senza considerare l'analisi del secondo ordine (e2), entrambi i punti si trovano in aree ombreggiate e ammissibili dove la verifica a flessione biassiale può essere trascurata. Quando si considera l'eccentricità secondo l'analisi del secondo ordine, l'eccentricità del carico biassiale è ridotta per il punto A, mentre per la posizione del carico B, la flessione biassiale viene aumentata e il carico viene spostato fuori dal campo consentito.
Verifica separata nella direzione dell'asse principale considerando l'interazione del momento biassiale
Se le condizioni dell'equazione 5.38a e dell'equazione 5.38b [1] non sono soddisfatte, i prerequisiti per la verifica separata nella direzione dell'asse principale senza considerare l'interazione del momento biassiale secondo 5.8.9 (2°). La sezione (4) del capitolo 5.8.9 [1] utilizza l'equazione 5.39 per descrivere un approccio semplificato che è possibile utilizzare per considerare l'interazione del momento biassiale con il progetto precedente delle singole direzioni dell'asse principale.
La seguente equazione 5.39 [1] tiene conto dell'interazione del momento in modo semplificato.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
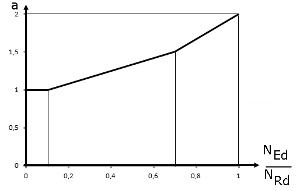
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
La figura 02 mostra l'esponente a in funzione del rapporto NEd/N Rd. NRd è il valore di progetto della resistenza assiale centrica e può essere determinato con NRd = Ac ⋅ fcd + As + fyd . Ac rappresenta l'area della sezione trasversale lorda, As rappresenta l'area di armatura longitudinale e fcd e fyd rappresentano le resistenze di progetto dei materiali utilizzati.
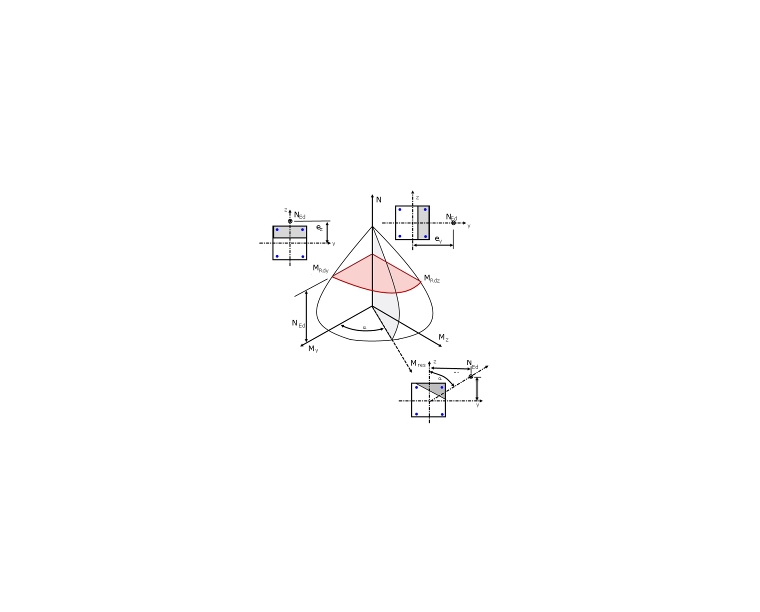
Quando si utilizza l'equazione 5.39 [1], si noti inoltre che le due resistenze a flessioneMRdy eMRdz devono essere prese dai diagrammi di interazione di progetto per le due direzioni principali quando si ha una forza assiale costante ( vedere la Figura 03).
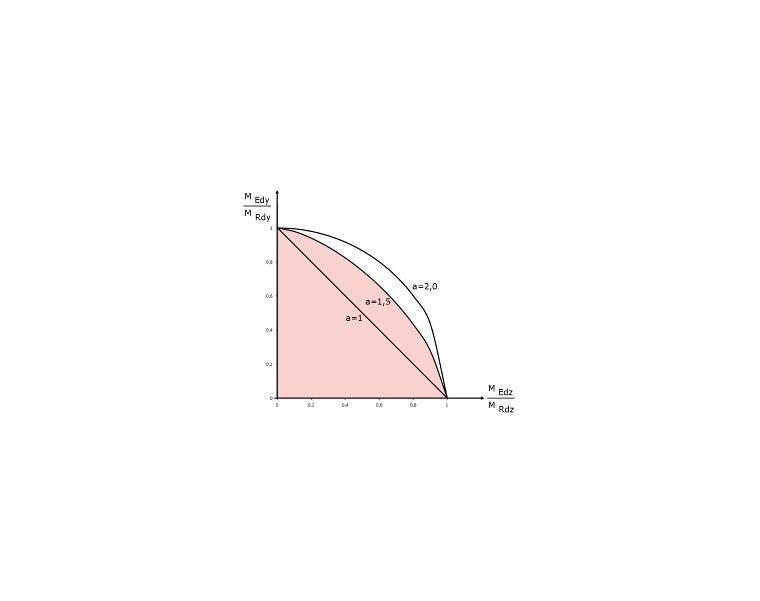
La figura 03 mostra un quadrante di un diagramma di interazione tridimensionale My-Mz-N. L'equazione 5.39 si basa sulla semplificazione di una sezione orizzontale a NEd utilizzando il diagramma di interazione 3D e generando un diagramma di interazione My-Mz dei momenti semplificato con l'esponente a. Nella figura 03, il diagramma di interazione dei momenti My-Mz per la forza assiale NEd (sezione orizzontale) è mostrato ombreggiato in rosso. Anche il diagramma di interazione semplificato secondo l'equazione 5.39 è ombreggiato in rosso per il confronto. La Figura 04 mostra, a seconda dell'esponente a, la distribuzione dell'interazione del momento applicata nell'equazione 5.39[1].
Il vantaggio di questo approccio semplificato secondo l'equazione 5.39[1] è che gli elementi compressi con eccentricità biassiale possono anche essere progettati rapidamente e facilmente per mezzo dei noti diagrammi di interazione MN per flessione uniassiale con assiale forza.
Progetto esatto della sezione trasversale con eccentricità del carico biassiale
Un progetto preciso di una sezione trasversale con forza assiale e flessione biassiale richiede un calcolo iterativo delle deformazioni della sezione trasversale. Il calcolo delle deformazioni della sezione trasversale è possibile solo con uno strumento di calcolo. Il progetto allo stato limite ultimo è soddisfatto se il carico è all'interno del diagramma di interazione Mres-N (zona grigia ombreggiata in figura 03) o nel diagramma del momento Mz-My determinato esattamente (area in rosso ombreggiata in figura 03). Determinando con precisione le curve limite, è possibile generare capacità di carico aggiuntive per il progetto.
Conclusione
Per un'eccentricità con carico biassiale, la norma consente diverse varianti di progetto a seconda della posizione del carico. Rispettando le condizioni al contorno delle equazioni 5.38a e 5.38b [1], l'interazione del momento biassiale può essere trascurata e la verifica può essere eseguita nelle direzioni dell'asse principale. Se si superano i limiti sopra menzionati, l'interazione del momento deve essere considerata nel progetto. Ciò è possibile in modo semplificato con la formula di interazione secondo l'equazione 5.39 [1] o mediante un'analisi della sezione trasversale biassiale esatta. Tutti gli approcci di progettazione descritti sono possibili con il modulo aggiuntivo RF-/CONCRETE Columns.