Общие сведения
Дополнительный модуль RF-/CONCRETE Columns позволяет рассчитать железобетонные сжатые элементы с помощью метода номинальной кривизны, как описано в пункте 5.8.8 нормы Еврокод 2. Другие нормативы описывают этот метод как метод модели колонны. В предыдущей статье подробно описано определение эксцентриситетов нагрузки, которые должны применяться при использовании метода номинальной кривизны. Поэтому определение отдельных эксцентриситетов здесь подробно описано не будет.
Отдельный расчет в направлении главной оси без учета взаимодействия двухосных моментов
Согласно 5.8.9 (2), EN 1992-1-1 {%://#Refer [1]]] , колонну с эксцентриситетом двухосной нагрузки можно рассчитать отдельно в обоих направлениях главных осей без учета взаимодействие моментов, если соблюдены пределы уравнений 5.38a и 5.38b [1]. Формулы описаны в статье по ссылке выше. Данные ограничения и подход к расчету основаны на том, что один из двух эксцентриситетов нагрузки является определяющим, а второй играет лишь второстепенную роль.
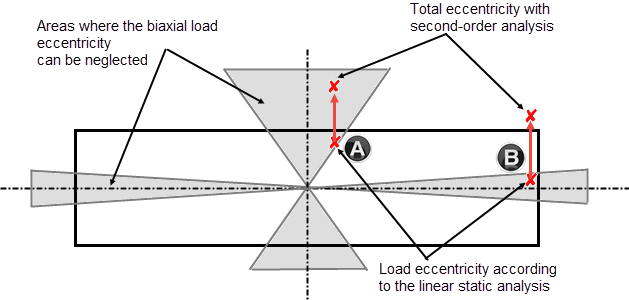
При расчете в отдельных направлениях главных осей дополнительный эксцентриситет от несовершенства должен учитываться только в решающем направлении. На рисунке 01 показаны, какие области не должны учитываться при двухосном изгибе. Если внецентренная нормальная сила находится в отмеченных областях, колонну можно рассчитать отдельно в обоих главных направлениях. Обратите внимание, что эксцентриситеты нагрузки должны учитываться по методу второго порядка в соответствующих направлениях главных осей.
Это также показано на рисунке 01. Точки A и B на рисунке 01 представляют два примера возможного положения нагрузки, когда влияние эксцентриситета, рассчитанного по методу второго порядка, имеет различные эффекты. Без учета расчета второго порядка (e2), обе точки расположены в отмеченных и допустимых областях, где расчетом двухосного изгиба можно пренебречь. Если учитывается эксцентриситет при расчете по методу второго порядка, эксцентриситет двухосной нагрузки уменьшается для точки А, тогда как для положения нагрузки B двухосный изгиб увеличивается, а нагрузка сдвигается из допустимого диапазона.
Отдельный расчет в направлении главной оси с учетом взаимодействия двухосных моментов
Если условия уравнения 5.38a и уравнения 5.38b [1] не выполнены, условия для отдельного расчета в направлении главной оси без учета взаимодействия двухосных моментов по 5.8.9 (2-ой ). Раздел 4, глава 5.8.9 [1] использует формулу 5.39 для описания упрощенного подхода, который можно использовать для учета взаимодействия двухосных моментов с предыдущим расчетом отдельных направлений главных осей.
Следующее уравнение 5.39 [1] учитывает взаимодействие моментов в упрощенном виде.
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
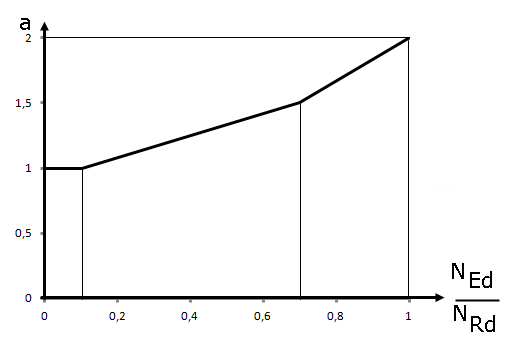
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
На рисунке 02 показана экспонента a как функция отношения NEd/NRd. NRd - расчетное значение сопротивления осевой нормальной силе, его можно определить с помощью NRd = Ac ⋅ fcd + As + fyd . Ac представляет собой общую площадь сечения, As представляет собой площадь продольной арматуры, а fcd и fyd представляют расчетные прочности используемых материалов.
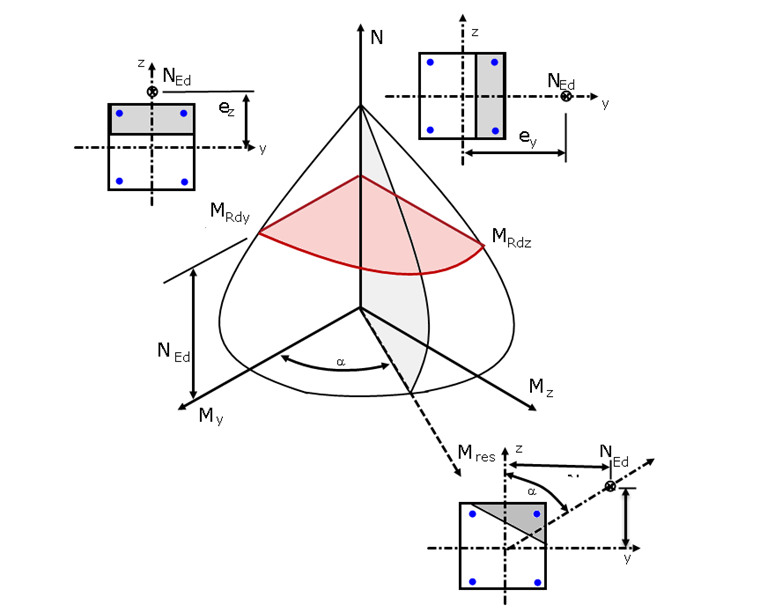
При использовании уравнения 5.39 [1], необходимо обратить внимание также на то, что два сопротивления изгибуMRdy иMRdz должны быть взяты из расчетных диаграмм взаимодействия для двух главных направлений при постоянной осевой силе ( см.Рисунок 03).
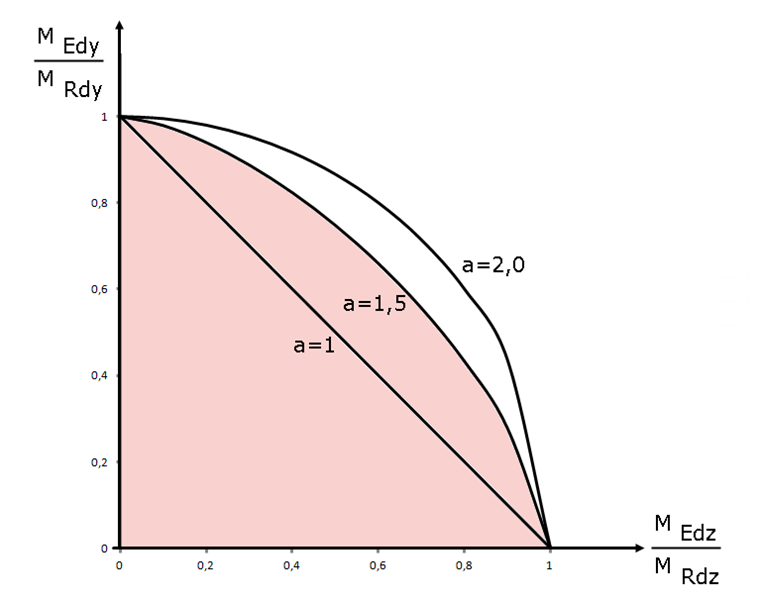
На рисунке 03 показан квадрант трехмерной диаграммы взаимодействия My-Mz-N. Формула 5.39 основана на упрощении горизонтального сечения до NEd, с использованием трехмерной диаграммы взаимодействия и создании упрощенной диаграммы взаимодействия моментов My-Mz с экспонентой а. На рисунке 03 фактическая диаграмма взаимодействия моментов My-Mz для осевой силы NEd (горизонтальное сечение) показана красным цветом. Упрощенная диаграмма взаимодействия по уравнению 5.39 также отмечена красным, для сравнения. На рисунке 04 показано, в зависимости от экспоненты a, распределение моментов взаимодействия, примененных в уравнении 5.39[1].
Преимущество данного упрощенного подхода в соответствии с уравнением 5.39[1] заключается в том, что сжатые элементы с двухосными эксцентриситетами могут быть быстро и легко рассчитаны с помощью известных диаграмм взаимодействия MN для одноосного изгиба с осевой сила.
Точный расчет сечения с эксцентриситетом двухосной нагрузки
Точный расчет сечения с нормальной силой и двухосным изгибом требует итеративного расчета деформаций сечений. Расчет этих деформаций сечений возможен только с помощью вычислительного инструмента. Расчет по предельным состояниям выполняется, если нагрузка находится внутри диаграммы взаимодействия Mres-N (серая область на рисунке 03) или точно заданной диаграммы моментов Mz-M y (красная область на рисунке 03). Благодаря точному заданию предельных кривых, можно создать дополнительную нагрузку для расчета.
Заключение
Для эксцентриситета двухосной нагрузки норматив допускает различные варианты расчета в зависимости от положения нагрузки. При соблюдении граничных условий из уравнений 5.38a и 5.38b {%ref#Refer [1]]], взаимодействием двухосных моментов можно пренебречь и расчет можно выполнить в направлениях главных осей. Если вышеприведенные пределы превышены, то взаимодействие моментов должно учитываться в расчетах. Это можно сделать упрощенно с помощью формулы взаимодействия по уравнению 5.39[1] или с помощью точного двухосного расчета сечения. Все описанные расчетные подходы возможны в дополнительном модуле RF-/CONCRETE Columns.