基本
附加模块 RF-/CONCRETE Columns 可以按照欧洲规范 2 第 5.8.8 章中规定的名义曲率法设计混凝土受压构件。 在其他规范中,这种方法被称为模型柱法。 在之前的一篇文章中详细介绍了使用名义曲率法计算荷载偏心 。 因此这里不再详细描述确定单个偏心。
基本主轴方向单独设计,不考虑双轴弯矩相关
根据 EN 1992-1-1 中 5.8.9 (2) 中的规定,{%于此参见[1]]],允许在两个主轴方向上分别设计具有双向荷载偏心的柱,而无需考虑弯矩相关性,如果满足公式 5.38a 和 5.38b [1] 在上面链接的文章中对公式进行了介绍。 得出这些限值和设计方法的基础是,荷载偏心其中一个为主导值,另一个为从属值。
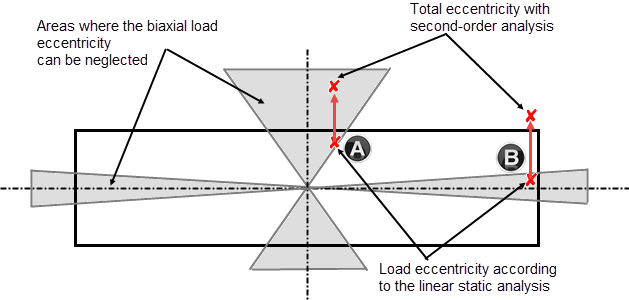
在单独的主轴方向上进行设计时,只能考虑主导方向上的缺陷引起的附加偏心距。 图 01 显示了双向受弯时不需要考虑的区域。 如果偏心轴力位于阴影区域内,则可以在两个主要方向上分别设计柱子。 二阶分析必须在各自的主轴方向上考虑荷载的偏心。
在图 01 中也有说明。 图 01 中的点 A 和 B 表示两个荷载位置的例子,根据二阶分析,偏心的影响有不同的效应。 在不考虑二阶分析 (e2 ) 的情况下,两个点位于阴影和双轴受弯设计可忽略的容许区域内。 根据二阶分析,当考虑偏心时,在点 A 减少双向荷载的偏心,而在荷载位置 B 增加双向弯曲,并且超出容许值范围。
考虑双轴弯矩共同作用,主轴方向单独设计
如果不满足公式 5.38a 和 5.38b {%! (2nd ). 章节 5.8.9 {%于#Refer [1]]] 中的(4)节使用公式 5.39 描述了一种考虑双向弯矩相互作用的简化方法,以前的设计是各个主轴方向[SCHOOL.INSTITUTION]
下面的公式 5.39 {%!
|
MEd,z/y |
Bemessungsmoment um die entsprechende Achse einschließlich des Moments nach Theorie II. Ordnung |
|
MRd,z/y |
Biegewiderstand um die entsprechende Achse |
|
a |
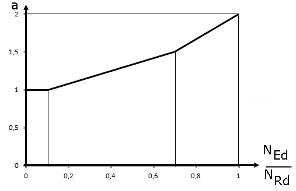
= 2 für runde und elliptische Querschnitte, gemäß Bild 02 für rechteckige Querschnitte |
图02 显示指数a关于比值NEd/NRd的函数。 NRd是中心轴承载力设计值,可以通过下式计算 NRd = Ac ⋅ fcd + As + fyd 。 Ac表示总截面面积,As表示纵向钢筋面积,fcd和 fyd表示所用材料的设计强度。
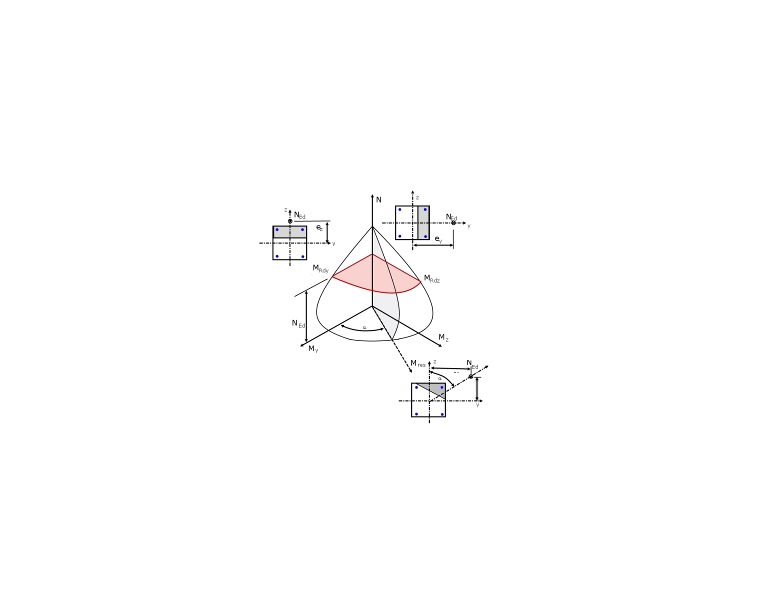
请注意,在使用公式 5.39 {%于#请参阅[1]]]时,两个抗弯承载力 MRdy和MRdz必须取自具有恒定轴力时 (见图 03)。
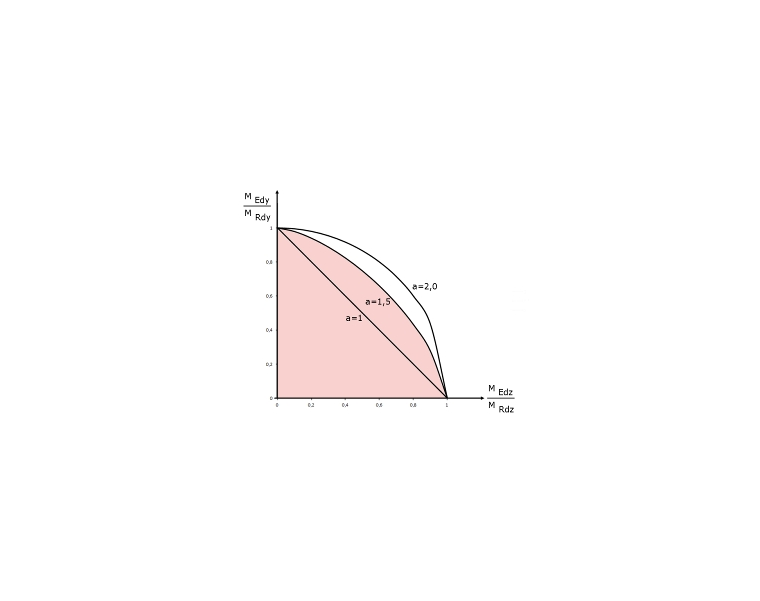
图03显示的是三维My -Mz -N相关性关系图的一个象限。 公式 5.39 是基于使用三维相互作用图对 NEd 的水平截面进行简化,并生成简化的 My -Mz弯矩相互作用图,指数为 a。 在图 03 中红色阴影部分显示了轴力为 NEd时的 My -Mz实际弯矩相关曲线(水平截面)。 为了便于比较,简化的相互作用图表也添加了红色阴影, 图 04 显示了公式 5.39 中弯矩相互作用相关的指数 a 的分布[1]。
根据公式 5.39{%39#参见 [1]]] 的这种简化方法的优点是,可以通过已知的单轴受弯和轴向受压的 MN 相关图快速方便地设计双轴偏心的受压构件。力。
考虑双向偏心荷载的精确截面设计
有时,对轴向受力和双向受弯的截面进行精确设计,需要对截面应变进行迭代计算。 只有使用软件可以计算截面应变。 如果荷载位于 Mres -N 相关性曲线(图 03 中灰色阴影区域)或 Mz -My弯矩曲线(图03 中红色阴影区域)内,则认为承载能力极限状态设计满足要求。 通过精确地确定极限曲线,可以为设计生成额外的承载力。
概述总结
对于双向荷载偏心,规范允许根据荷载位置的不同有不同的设计变体。 根据公式 5.38a 和 5.38b 的边界条件 [1],可以忽略双向弯矩的相关性,在主轴方向进行设计。 如果超过上述限制,则在设计中必须考虑弯矩的相关作用。 这可以根据公式 5.39 中的相关性公式或精确的双向轴截面分析以简化的计算方式实现。 介绍的所有设计方法都可以在附加模块 RF-/CONCRETE Columns 中实现。