A estabilidade da estrutura não é um fenômeno novo quando se refere ao projeto de aço. O padrão canadense de projeto de aço CSA S16 e a versão mais recente de 2019 não são exceções. Os requisitos detalhados de estabilidade podem ser abordados com o Método de Análise de Estabilidade Simplificada na Cláusula 8.4.3 ou, novidade do padrão de 2019, o método de Efeitos de Estabilidade na Análise Elástica fornecido no Anexo O [1].
A Cláusula 8.4.1 [1] lista os requisitos de estabilidade que o projeto estrutural deve abordar usando qualquer um dos métodos. Estes incluem deformações que contribuem para a estrutura, efeitos de segunda ordem, incluindo P-Δ e P-δ, imperfeições geométricas globais e de membro, redução de rigidez com base no escoamento do membro e tensões residuais e, por último, incerteza na rigidez e resistência da estrutura.
Cláusula 8.4.3 – Método de Análise de Estabilidade Simplificada
Com o método de análise de estabilidade simplificada dado na 8.4.3 [1], apenas alguns requisitos são listados.
Não-linearidades Geométricas
O primeiro inclui efeitos de segunda ordem nos membros, ou P-Δ, que podem ser diretamente considerados na análise. Um método de cálculo de análise de segunda ordem é mais comum com muitos programas de análise estrutural atualmente. A alternativa é amplificar todas as cargas axiais dos membros e momentos de flexão obtidos de uma análise de primeira ordem pelo fator U2 definido em 8.4.3.2(b) [1]. Esta abordagem pode ser mais adequada para cálculos manuais ou se o software de análise estrutural não incluir automaticamente os efeitos P-Δ.
Imperfeições Geométricas
Cargas laterais noções são o segundo item listado sob o método simplificado na Cláusula 8.4.3.3 [1]. Esta carga aplicada é igual a 0.005 vezes a carga gravitacional total ponderada no andar considerado e deve ser distribuída de forma semelhante à carga gravitacional. Cargas noções são sempre aplicadas na direção que gera o maior efeito de desestabilização. Isso significa que tais cargas devem ser aplicadas na mesma direção que uma carga de vento lateral para gerar as maiores deformações e forças internas na estrutura.
Anexo O.2 – Efeitos de Estabilidade na Análise Elástica
Como alternativa à abordagem simplificada de análise de estabilidade acima, engenheiros podem utilizar o Anexo O.2 para satisfazer os requisitos de estabilidade estabelecidos na Cláusula 8.4.1 [1]. Esta abordagem foi adicionada ao padrão de 2019 e tem muitas semelhanças com o manual de projeto de aço dos EUA AISC 360-16 Ch. C Método de Análise Direta.
Não-linearidades Geométricas
Não-linearidades geométricas, ou efeitos de segunda ordem, são abordadas em O.2.2 [1]. Como o método simplificado, uma análise de segunda ordem pode ser realizada diretamente, o que inclui os efeitos das cargas atuando nos pontos de intersecção deslocados dos membros (efeitos P-Δ). Adicionalmente, os efeitos das cargas axiais atuando na forma defletida do membro ao longo do comprimento devem ser considerados (P-δ). Existem disposições dadas em O.2.2 [1] onde P-δ pode ser totalmente negligenciado. Por outro lado, se P-δ for incluído diretamente na análise, o fator U1 pode ser definido como 1.0 usado na Cláusula 13.8 - Design de membro sob compressão axial e flexão [1].
Imperfeições Geométricas
Imperfeições geométricas dos membros, como fora de alinhamento dos membros ou imperfeições geométricas locais, como fora de alinhamento do elemento para membros, não precisam ser consideradas ao projetar conforme a Cláusula O.2 [1]. No entanto, imperfeições geométricas globais devem ser consideradas com modelagem direta ou com o uso de cargas laterais noções. Existe a exceção, porém, de que essas imperfeições geométricas globais podem ser negligenciadas apenas para combinações de cargas laterais se cumprirem os requisitos estabelecidos na Cláusula O.2.3.1 [1]. Entre os requisitos estão que as cargas gravitacionais da estrutura sejam suportadas principalmente por elementos estruturais verticais e que a relação entre o máximo deslocamento de andar de 2ª ordem para o de 1ª ordem usando rigidez de membro reduzida de acordo com a Cláusula O.2.4 [1] não exceda 1.7 em qualquer nível de andar.
Quando o engenheiro não pode negligenciar essas imperfeições, o primeiro método de modelagem direta pode ser usado. Pontos de interseção de membros devem ser deslocados de suas localizações originais. A amplitude deste deslocamento inicial é estabelecida na Cláusula 29.3 [1] e aplicada na direção de maior desestabilização, que para a maioria das estruturas de edifícios é uma tolerância de 1/500 para desalinhamento de colunas. O problema significativo com este método é o alto número de cenários de modelagem que devem ser considerados. Teoricamente, quatro deslocamentos são necessários nas quatro diferentes direções em cada nível de andar. Se os efeitos de desalinhamento dos membros também forem acoplados com desalinhamento das colunas, isso adiciona muitos mais cenários de modelagem a serem considerados para atender ao maior efeito de desestabilização.
O método alternativo e preferencial para imperfeições geométricas globais é aplicar cargas laterais noções. Este método é permitido apenas quando as cargas gravitacionais são suportadas principalmente por elementos estruturais verticais. Cargas laterais noções foram abordadas anteriormente neste artigo e são aplicadas da mesma maneira que a análise de estabilidade simplificada na Cláusula 8.4.3.2 [1]. No entanto, a amplitude é reduzida de 0.005 para 0.002 vezes a carga gravitacional ponderada no andar relevante. A redução na magnitude é permitida na Cláusula O.2.3.3, pois estas cargas noções contabilizam apenas as imperfeições geométricas globais, enquanto cargas noções na Cláusula 8.4.3.2 [1] também contabilizam efeitos de inelasticidade e outras incertezas.
Efeitos de Inelasticidade
Para contabilizar os efeitos de inelasticidade e também considerar imperfeições geométricas locais ou iniciais de membro, assim como incerteza na rigidez e resistência, rigidez axial e flexional reduzida do membro de acordo com as seguintes equações na Cláusula O.2.4 [1] deve ser aplicada aos membros que contribuem para a estabilidade lateral.
- EAr = 0.8τbEA
- EIr = 0.8τbEI
onde
- Cf/Cy < 0.5 ; τb = 1.0
- Cf/Cy > 0.5 ; τb = 4Cf/Cy(1-Cf/Cy)
Para evitar distorções locais, o padrão sugere aplicar esta redução de rigidez a todos os membros. Além disso, quando a rigidez ao cisalhamento (GA) e a rigidez à torção (GJ) contribuem significativamente para a estabilidade lateral, a redução da rigidez deve ser considerada. A redução da rigidez não deve ser usada ao analisar deslocamentos, deflexões, vibrações ou vibrações naturais.
Aplicação do Anexo O.2 no RFEM 6
O novo programa de EFA, RFEM 6, incorpora os últimos requisitos de estabilidade da norma CSA S16:19 de acordo com as disposições do Anexo O.2.
Não-linearidades Geométricas
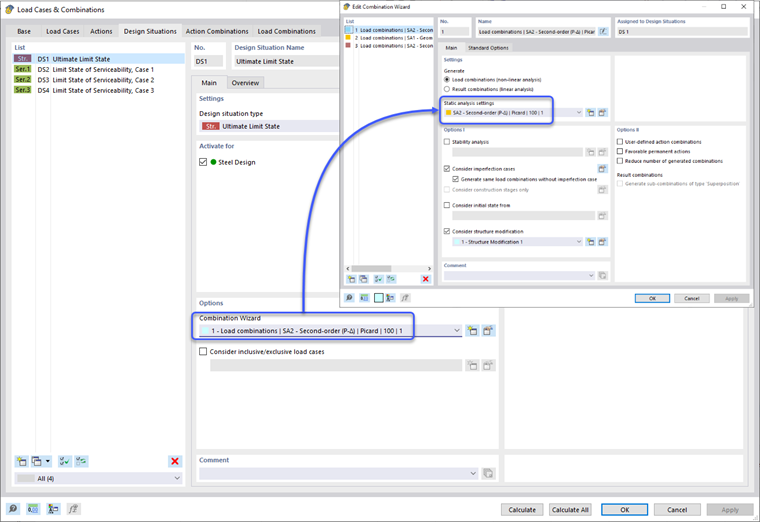
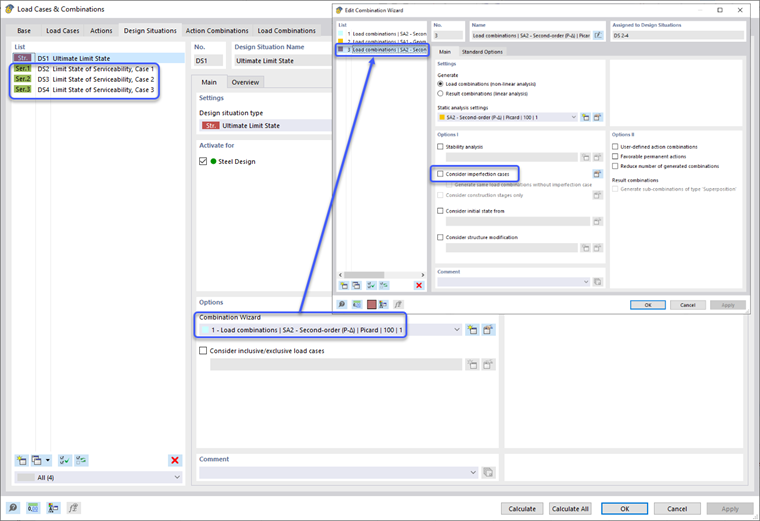
Os efeitos de segunda ordem estabelecidos na Cláusula O.2.2 [1] são considerados diretamente quando o método de cálculo da análise estática é definido como “Segunda ordem (P-Δ)”. Isso pode ser aplicado nas opções do Assistente de Combinação de Situação de Projeto. Por sua vez, todas as combinações de cargas sob a Situação de Projeto serão automaticamente definidas também para uma análise de segunda ordem. O usuário tem a opção de modificar individualmente as configurações de análise estática de uma combinação de carga, se preferir.
Não apenas os efeitos P-Δ são incluídos para a análise do membro, mas também os P-δ são automaticamente considerados. Para mais informações sobre este tópico e verificação no RFEM 6, consulte: Base de dados de conhecimento 1759 .
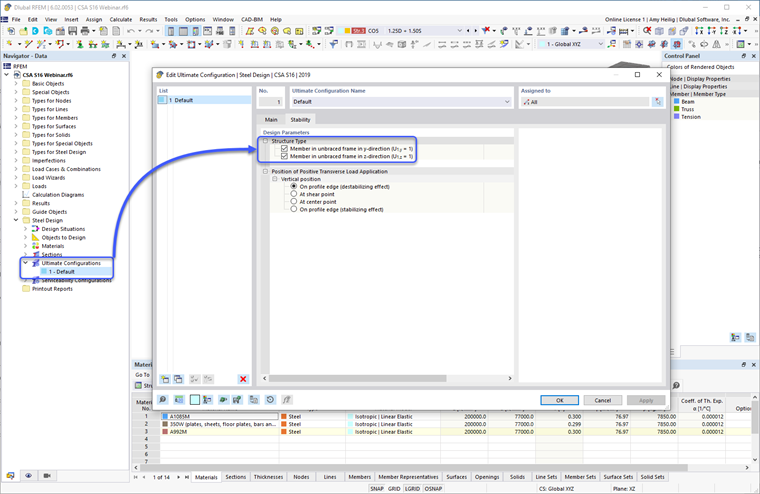
Portanto, o fator U1 pode ser definido como 1.0 especificado na Cláusula 13.8 para o design do membro de aço. Esta opção é encontrada sob o complemento Design de Aço – Configurações Ultimativas – Estabilidade – Parâmetros de Design.
Imperfeições Geométricas
O usuário do RFEM 6 tem a opção de modelar diretamente imperfeições geométricas globais deslocando pontos ou nós de interseções de membros. No entanto, para garantir que este método crie o maior efeito de desestabilização, múltiplos modelos com vários cenários precisarão ser realizados. Isso é bastante demorado e complicado.
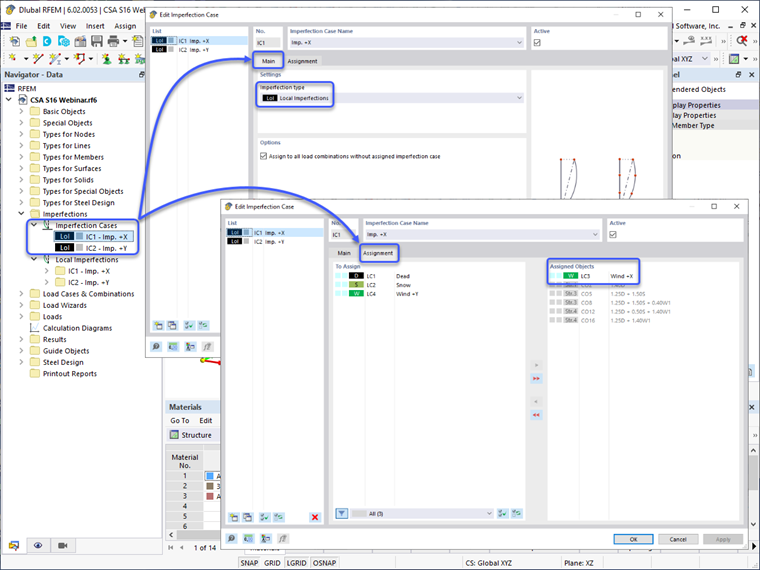
A abordagem alternativa é aplicar cargas noções com as opções de imperfeição fornecidas no RFEM 6. Para começar, Casos de Imperfeição com o tipo de imperfeição definido como “Imperfeições locais” sob a aba Principal devem ser definidos primeiro. Estes tipicamente incluem casos nas direções ortogonais X e Y, dependendo da aplicação de cargas laterais, como ventos e sísmicas. O Caso de Imperfeição pode então ser correlacionado sob a aba Atribuição aos casos de carga específicos para produzir o maior efeito de desestabilização (por exemplo, cargas noções na direção +X devem ser aplicadas apenas com cargas de vento na direção +X).
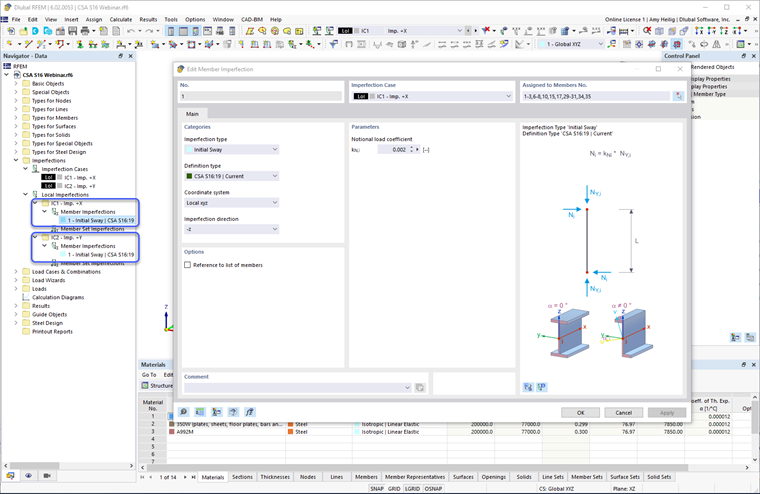
Depois que os Casos de Imperfeição são gerados, as imperfeições dos membros podem ser definidas. A caixa de diálogo de Imperfeições do Membro inclui a CSA S16:19 nas opções do menu suspenso. A carga noção é aplicada na extremidade do membro (ou seja, topo da coluna) com uma magnitude igual a 0.002 (ou 0.005 se usando o método de estabilidade simplificado) multiplicado pela força axial do membro (carga gravitacional aplicada no membro). Uma força igual e oposta é aplicada internamente na extremidade oposta do membro para evitar forçar de base irreais. A definição de imperfeição é aplicada aos eixos locais dos membros na mesma direção que a carga lateral aplicada, como vento ou sísmica. A definição é ainda aplicada a todos os membros verticais no modelo.
Depois que as imperfeições são aplicadas ao modelo, a Situação de Projeto é definida por padrão para considerar imperfeições para todas as combinações de carga. Imperfeições devem ser aplicadas às Situações de Design Ultimativo, mas desativadas para as Situações de Design de Serviço. Isso pode ser configurado criando um novo tipo de definição do Assistente de Combinação, desativando as opções de consideração de imperfeições e aplicando apenas às Situações de Design de Serviço.
Efeitos de Inelasticidade
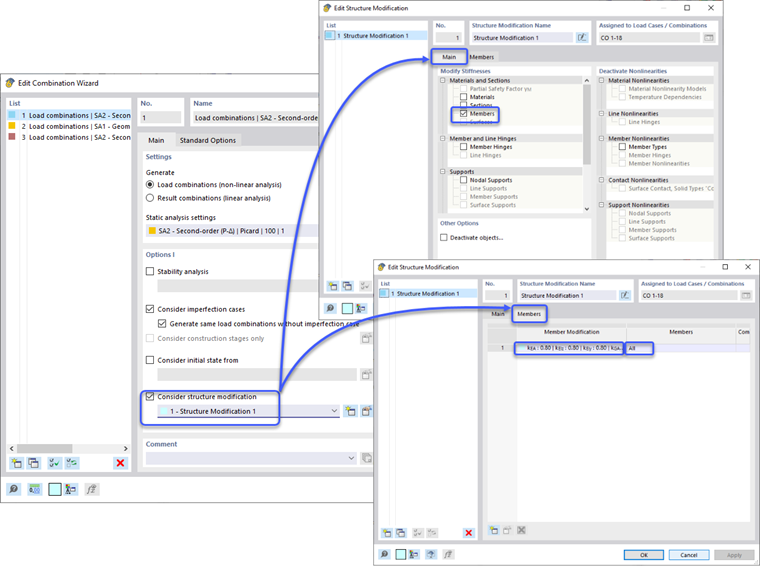
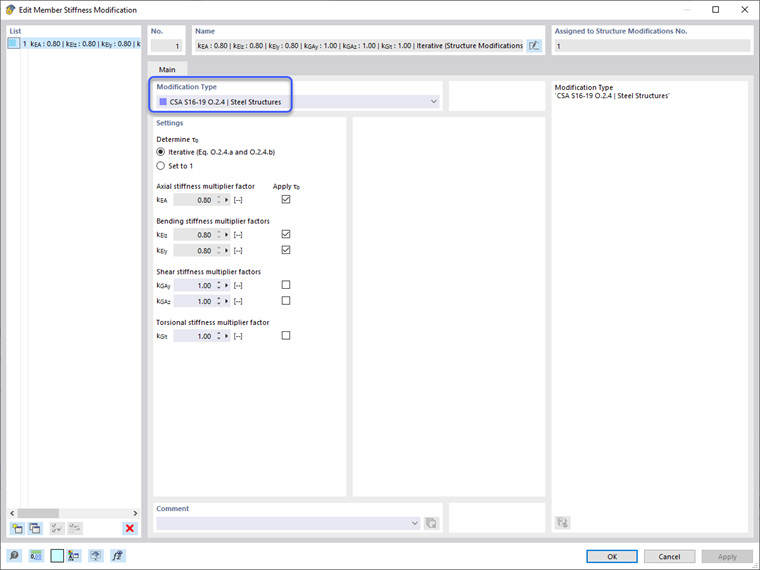
Reduções de rigidez são aplicadas apenas à Situação de Design Ultimativo, uma vez mais através das opções de definição do Assistente de Combinação e a caixa de seleção “Considerar modificação da estrutura”. Uma nova definição de modificação da estrutura pode ser criada. A caixa de seleção “Membros” é selecionada sob a aba Principal - Materiais e Seções. Isso traz uma nova aba de Membros onde a definição de Modificação de Rigidez do Membro é definida de acordo com o CSA S1-19 O.2.4 | Estruturas de Aço. Este tipo de definição permite que o programa calcule automaticamente o fator de redução τb, ou um valor generalizado de 1.0 pode ser definido para todos os membros. Além disso, o fator 0.8 pode ser aplicado aos vários tipos de rigidezes dos membros. O usuário pode determinar se o fator τb e 0.8 deve ser aplicado somente à rigidez axial e de flexão do membro ou se a rigidez ao cisalhamento e à torção também deve ser considerada. Uma vez que as propriedades de modificação da rigidez são inseridas, a definição pode ser aplicada a membros específicos ou o termo “Todos” pode ser configurado para aplicar a todos os membros no modelo.
Como a redução da rigidez do membro não deve ser considerada para o design de serviço (por exemplo, verificações de deflexão), a caixa de seleção “Considerar modificação da estrutura” deve permanecer desmarcada para a definição do Assistente de Combinação de Situação de Design de Serviço.
Após essas modificações, todas as combinações de carga ponderadas incluirão a redução de rigidez de modificação da estrutura enquanto todas as combinações de carga não ponderadas usarão a rigidez completa do membro.
Resumo
Requisitos significativos de design de estabilidade de acordo com o Anexo O.2 do manual de projeto de aço canadense CSA S16:19 são totalmente incorporados no fluxo de trabalho de análise do RFEM 6. Mais notavelmente, esses requisitos incluem uma análise de segunda ordem, a capacidade de considerar cargas noções como imperfeições, bem como rigidezes de membros reduzidas. Para ver este tópico demonstrado em um vídeo de exemplo detalhado, confira o webinar: Dimensionamento de aço segundo a norma CSA S16:19 no RFEM 6 (EUA) .