La estabilidad estructural no es un fenómeno nuevo cuando se refiere al diseño en acero. El estándar canadiense de diseño en acero CSA S16 y su versión más reciente de 2019 no es una excepción. Se pueden abordar requisitos detallados de estabilidad con el Método Simplificado de Análisis de Estabilidad en la Cláusula 8.4.3 o, nuevo para el estándar de 2019, el método de Efectos de Estabilidad en Análisis Elástico proporcionado en el Anexo O [1].
La Cláusula 8.4.1 [1] enumera los requisitos de estabilidad que el diseño estructural debe abordar utilizando cualquiera de los métodos. Estos incluyen deformaciones que contribuyen a la estructura, efectos de segundo orden que incluyen P-Δ y P-δ, imperfecciones geométricas globales y de los miembros, reducción de rigidez teniendo en cuenta el fluencia de los miembros y tensiones residuales, y por último, la incertidumbre en la rigidez y resistencia de la estructura.
Cláusula 8.4.3 – Método Simplificado de Análisis de Estabilidad
Con el método simplificado de análisis de estabilidad dado en 8.4.3 [1], sólo se enumeran un par de requisitos.
No linealidades geométricas
El primero incluye los efectos de segundo orden de los miembros, o P-Δ, que pueden considerarse directamente en el análisis. Un método de cálculo de análisis de segundo orden es el más común hoy en día con muchos programas de análisis estructural. La alternativa es amplificar todas las cargas axiales de los miembros y los momentos de flexión obtenidos de un análisis de primer orden mediante el factor U2 definido en 8.4.3.2(b) [1]. Este enfoque puede ser más adecuado para cálculos manuales o si el software de análisis estructural no incluye automáticamente los efectos P-Δ.
Imperfecciones geométricas
Las cargas laterales no reales son el segundo elemento enumerado bajo el método simplificado en la Cláusula 8.4.3.3 [1]. Esta carga aplicada es igual a 0.005 veces la carga total de gravedad factorizada en el piso considerado y debe distribuirse de manera similar a la carga de gravedad. Las cargas no reales siempre se aplican en la dirección que genera el mayor efecto desestabilizador. Esto significa que tales cargas deben aplicarse en la misma dirección que una carga de viento lateral para generar las mayores deformaciones y fuerzas internas en la estructura.
Anexo O.2 – Efectos de Estabilidad en Análisis Elástico
Como alternativa al enfoque de análisis de estabilidad simplificado mencionado arriba, los ingenieros pueden utilizar el Anexo O.2 para cumplir con los requisitos de estabilidad establecidos en la Cláusula 8.4.1 [1]. Este enfoque se agregó al estándar de 2019 y tiene muchas similitudes con el manual de diseño en acero de EE. UU. AISC 360-16 Ch. C Método de Análisis Directo.
No linealidades geométricas
Las no linealidades geométricas, o efectos de segundo orden, se abordan en O.2.2 [1]. Al igual que el método simplificado, se puede llevar a cabo directamente un análisis de segundo orden que incluya los efectos de las cargas actuando en los puntos desplazados de intersección de los miembros (efectos P-Δ). Además, se deben considerar los efectos de las cargas axiales actuando en la forma deflectada del miembro a lo largo de su longitud (P-δ). Se dan disposiciones en O.2.2 [1] donde P-δ puede omitirse por completo. Por otro lado, si P-δ se incluye directamente en el análisis, el factor U1 puede establecerse en 1.0 usado en la Cláusula 13.8 - Diseño de miembros en compresión axial y flexión [1].
Imperfecciones geométricas
Las imperfecciones geométricas de los miembros, como la falta de rectitud del miembro o las imperfecciones geométricas locales, como la falta de rectitud del elemento para los miembros, no necesitan considerarse al diseñar según la Cláusula O.2 [1]. Sin embargo, las imperfecciones geométricas globales deben considerarse con el modelado directo o con el uso de cargas laterales no reales. Existe la excepción, sin embargo, de que estas imperfecciones geométricas globales pueden omitirse para las combinaciones de cargas laterales sólo si cumplen con los requisitos establecidos en la Cláusula O.2.3.1 [1]. Entre los requisitos se encuentra que las cargas de gravedad de la estructura se sostienen principalmente por elementos estructurales verticales y que la proporción entre la deriva máxima del piso de segundo orden respecto a la deriva de piso de primer orden utilizando rigidez reducida del miembro según la Cláusula O.2.4 [1] no excede 1.7 en ningún nivel de piso.
Cuando el ingeniero no puede ignorar estas imperfecciones, se puede utilizar el primer método de modelado directo. Los puntos de intersección de los miembros deben desplazarse de sus ubicaciones originales. La amplitud de este desplazamiento inicial se establece en la Cláusula 29.3 [1] y se aplica en la dirección de mayor desestabilización, que para la mayoría de las estructuras de edificios es una tolerancia de 1/500 para la desviación de columnas. El problema significativo con este método es la cantidad alta de escenarios de modelos que deben considerarse. Teóricamente, se necesitan cuatro desplazamientos en las cuatro direcciones diferentes en cada nivel de piso. Si los efectos de la falta de rectitud del miembro también se combinan con la desviación de la columna, esto añade muchos más escenarios de modelado a considerar para lograr el mayor efecto desestabilizador.
El método alternativo y preferido para las imperfecciones geométricas globales es aplicar cargas laterales no reales. Este método solo está permitido cuando las cargas de gravedad son sostenidas principalmente por elementos estructurales verticales. Las cargas laterales no reales se trataron anteriormente en este artículo y se aplican de la misma manera que el análisis de estabilidad simplificado en la Cláusula 8.4.3.2 [1]. Sin embargo, la amplitud se reduce de 0.005 a 0.002 veces la carga de gravedad factorizada en el piso relevante. La reducción en magnitud es permitida en la Cláusula O.2.3.3 ya que estas cargas no reales solo cuentan para las imperfecciones geométricas globales, mientras que las cargas no reales en la Cláusula 8.4.3.2 [1] también cuentan para los efectos de inelasticidad y otras incertidumbres.
Efectos de inelasticidad
Para tener en cuenta los efectos de inelasticidad y también dar consideración a las imperfecciones iniciales del miembro o imperfecciones geométricas locales así como a la incertidumbre en rigidez y resistencia, se debe aplicar una reducción en la rigidez axial y de flexión de los miembros según las siguientes ecuaciones en la Cláusula O.2.4 [1] para los miembros que contribuyen a la estabilidad lateral.
- EAr = 0.8τbEA
- EIr = 0.8τbEI
donde
- Cf/Cy < 0.5 ; τb = 1.0
- Cf/Cy > 0.5 ; τb = 4Cf/Cy(1-Cf/Cy)
Para evitar distorsiones localizadas, el estándar sugiere aplicar esta reducción de rigidez a todos los miembros. Además, cuando la rigidez al corte (GA) y la rigidez torsional (GJ) contribuyen significativamente a la estabilidad lateral, se debe considerar la reducción de rigidez. La reducción de rigidez no debe usarse al analizar derivas, deflexiones, vibraciones o vibraciones naturales.
Aplicación del Anexo O.2 en RFEM 6
El nuevo programa de análisis por elementos finitos RFEM 6 incorpora los últimos requisitos de estabilidad del estándar CSA S16:19 según las disposiciones del Anexo O.2.
No linealidades geométricas
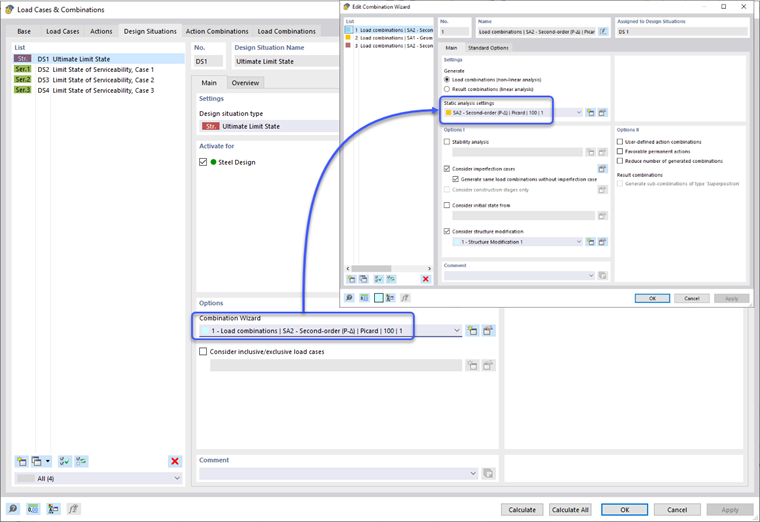
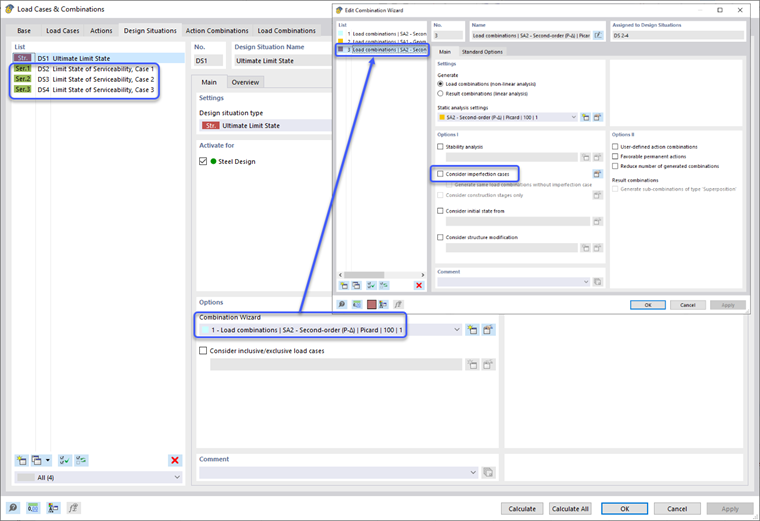
Los efectos de segundo orden establecidos en la Cláusula O.2.2 [1] se consideran directamente cuando el método de cálculo de análisis estático se establece en "Segundo orden (P-Δ)". Esto se puede aplicar en las opciones del Asistente de Combinación de Situación de Diseño. A su vez, todas las combinaciones de carga bajo la Situación de Diseño se configurarán automáticamente para un análisis de segundo orden también. El usuario tiene la opción de modificar individualmente la configuración de análisis estático de una combinación de carga si se prefiere.
No solo se incluyen los efectos P-Δ para el análisis de los miembros, sino que también se consideran automáticamente los P-δ. Para obtener más información sobre este tema y su verificación en RFEM 6, consulte: Base de conocimientos 1759 .
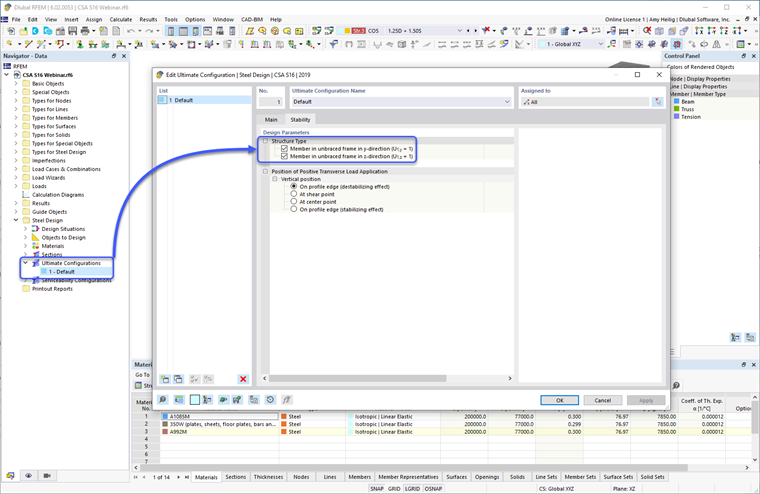
Por lo tanto, el factor U1 se puede establecer en 1.0 especificado en la Cláusula 13.8 para el diseño de miembros de acero. Esta opción se encuentra bajo el complemento de Diseño en Acero – Configuraciones Últimas – Estabilidad – Parámetros de Diseño.
Imperfecciones geométricas
El usuario de RFEM 6 tiene la opción de modelar directamente imperfecciones geométricas globales desplazando puntos o nodos de intersección de miembros. Sin embargo, para garantizar que este método cree el mayor efecto desestabilizador, será necesario llevar a cabo múltiples modelos con varios escenarios. Esto es bastante tedioso y requiere mucho tiempo.
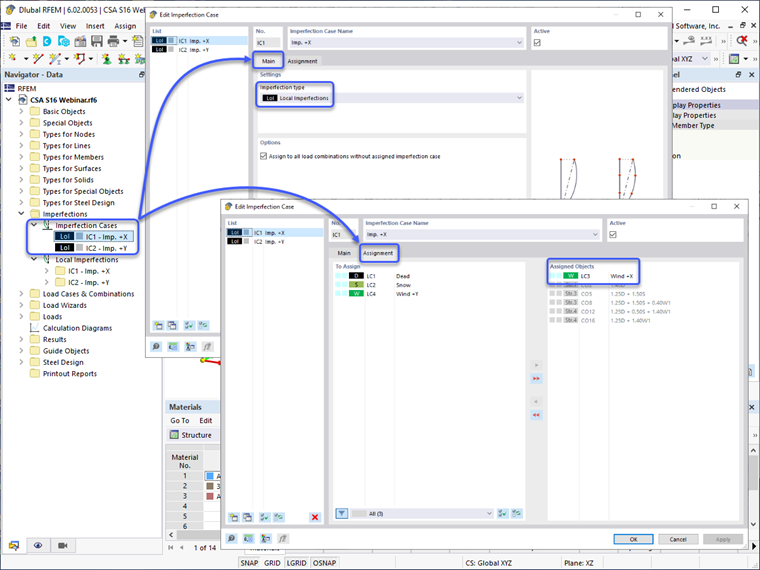
El enfoque alternativo es aplicar cargas no reales con las opciones de imperfección proporcionadas en RFEM 6. Para comenzar, primero deben definirse Casos de Imperfección con el tipo de imperfección configurado en "Imperfecciones locales" bajo la pestaña Principal. Estos normalmente incluirían casos en las direcciones ortogonales X y Y, dependiendo de la aplicación de cargas laterales como viento y sísmicas. El Caso de Imperfección puede luego correlacionarse bajo la pestaña Asignación a los casos específicos de carga para producir el mayor efecto desestabilizador (por ejemplo, las cargas no reales en la dirección +X sólo deben aplicarse con cargas de viento en la dirección +X).
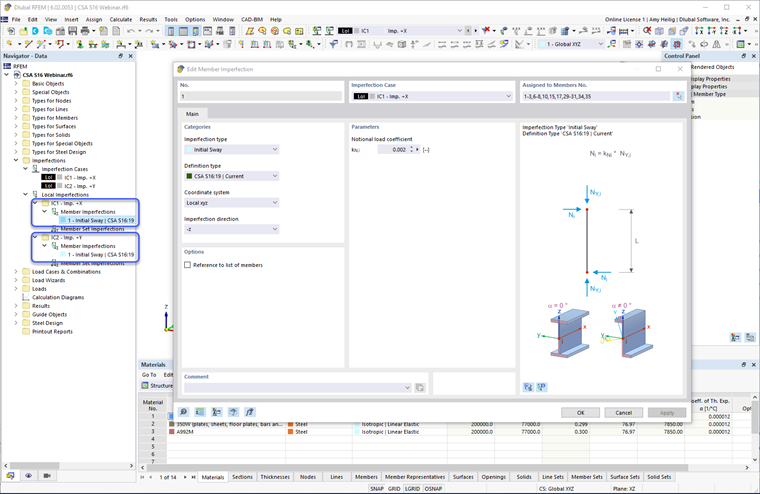
Después de generar los Casos de Imperfección, se pueden definir las imperfecciones de los miembros. El cuadro de diálogo de Imperfecciones de los Miembros incluye el CSA S16:19 en las opciones desplegables. La carga no real se aplica al extremo del miembro (es decir, la parte superior de la columna) con una magnitud igual a 0.002 (o 0.005 si se usa el método simplificado de estabilidad) multiplicado por la fuerza axial del miembro (carga de gravedad aplicada al miembro). Se aplica internamente una fuerza igual y opuesta en el extremo opuesto del miembro para evitar esfuerzos base no realistas. La definición de imperfección se aplica a los ejes locales de los miembros en la misma dirección que la carga lateral aplicada como viento o sísmica. La definición se aplica además a todos los miembros verticales en el modelo.
Después de aplicar las imperfecciones al modelo, la Situación de Diseño se configura por defecto para considerar imperfecciones para todas las combinaciones de carga. Las imperfecciones deben aplicarse a las Situaciones de Diseño Últimas pero desactivarse para las Situaciones de Diseño de Servicio. Esto se puede establecer creando un nuevo tipo de definición de Asistente de Combinación, desactivando las opciones de consideración de imperfecciones y aplicándolas solo a las Situaciones de Diseño de Servicio.
Efectos de inelasticidad
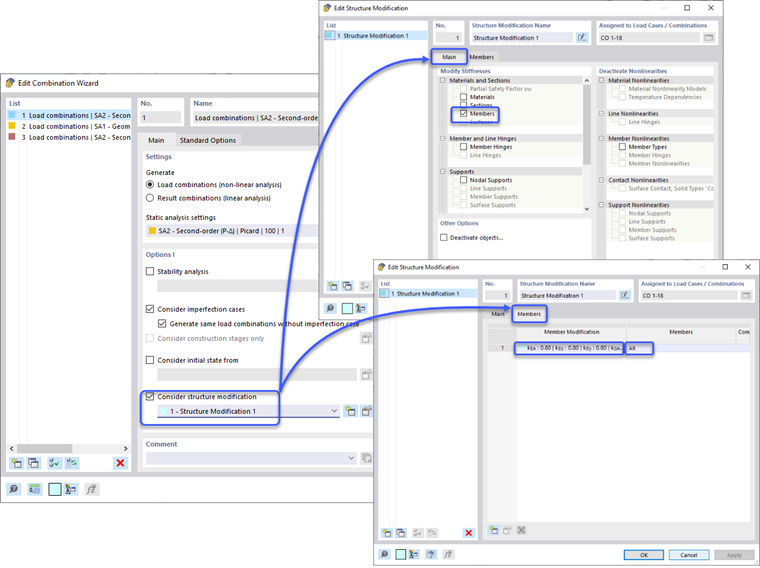
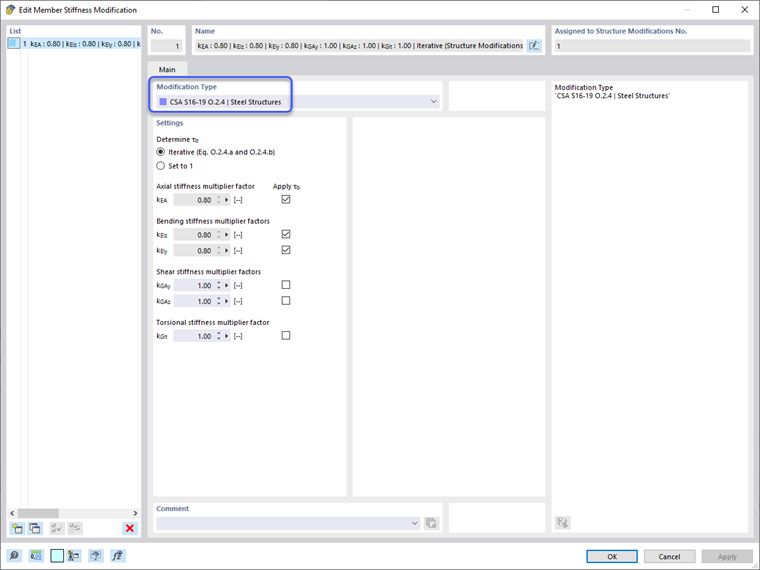
Las reducciones de rigidez se aplican a la Situación de Diseño Última solo una vez más a través de las opciones de definición del Asistente de Combinación y la casilla de verificación "Considerar modificación de la estructura". Se puede crear una nueva definición de modificación de la estructura. La casilla de verificación de "Miembros" se selecciona en la pestaña Principal - Materiales y Secciones. Esto abre una nueva pestaña de Miembros donde se define la Modificación de Rigidez de Miembros según la CSA S16-19 O.2.4 | Estructuras de Acero. Este tipo de definición permite que el programa calcule automáticamente el factor de reducción τb, o se puede configurar un valor generalizado de 1.0 para todos los miembros. Además, el factor 0.8 se puede aplicar a los diferentes tipos de rigidez de los miembros. El usuario puede determinar si el factor τb y el factor 0.8 deben aplicarse solo a la rigidez axial y de flexión del miembro o si también se debe considerar la rigidez al corte y torsional. Una vez que se ingresan las propiedades de modificación de rigidez, la definición se puede aplicar a miembros específicos o se puede establecer el término "Todos" para aplicarse a todos los miembros en el modelo.
Debido a que no se debe considerar la reducción de rigidez de los miembros para el diseño de servicio (por ejemplo, verificaciones de deflexión), la casilla de verificación "Considerar modificación de la estructura" debe permanecer sin marcarse para la definición del Asistente de Combinación de Situación de Diseño de Servicio.
Después de estas modificaciones, todas las combinaciones de carga factorizadas incluirán la reducción de rigidez de modificación de la estructura mientras que todas las combinaciones de carga no factorizadas usarán la rigidez completa de los miembros.
Resumen
Los requisitos significativos de diseño de estabilidad según el Anexo O.2 del manual de diseño en acero canadiense CSA S16:19 están completamente incorporados en el flujo de trabajo de análisis de RFEM 6. Más notablemente, estos requisitos incluyen un análisis de segundo orden, la capacidad de considerar cargas no reales como imperfecciones, así como rigideces de miembros reducidas. Para ver este tema demostrado en un video de ejemplo detallado, consulte el webinar: Cálculo de acero según CSA S16:19 en RFEM 6 (EE. UU.) .