Stabilita konstrukcí není novým jevem, pokud jde o návrh ocelových konstrukcí. Kanadská norma pro návrh ocelových konstrukcí CSA S16 a její nejnovější vydání z roku 2019 nejsou výjimkou. Podrobné požadavky na stabilitu lze řešit buď pomocí Metody zjednodušené analýzy stability v klauzuli 8.4.3 nebo, nově v normě 2019, pomocí metody Vlivy stability v elastické analýze, která je uvedena v Příloze O [1].
Klauzule 8.4.1 [1] uvádí požadavky na stabilitu, které by měl návrh konstrukce řešit pomocí jedné z uvedených metod. Ty zahrnují deformace přispívající ke stabilitě konstrukce, efekty druhého řádu včetně P-Δ a P-δ, globální a členské geometrické imperfekce, snížení tuhosti zohledňující protažení prvků a zbytková napětí a nakonec nejistotu v tuhosti a pevnosti konstrukce.
Klauzule 8.4.3 – Metoda zjednodušené analýzy stability
S metodou zjednodušené analýzy stability uvedenou v klauzuli 8.4.3 [1] je uvedeno jen několik požadavků.
Geometrické nelinearity
První zahrnují členské efekty druhého řádu, nebo P-Δ, které lze přímo zvážit v analýze. Metoda výpočtu analýzy druhého řádu je dnes nejběžnější pomocí mnoha softwarových programů pro analýzu konstrukcí. Alternativou je zvýšit všechny členské axiální zatížení a ohybové momenty získané z analýzy prvního řádu faktorem U2 definovaným v klauzuli 8.4.3.2(b) [1]. Tento přístup může být lépe přizpůsoben pro ruční výpočty nebo pokud softwar pro analýzu konstrukcí automaticky nezahrnuje efekty P-Δ.
Geometrické imperfece
Neúčetní boční zatížení jsou druhou položkou uvedenou pod zjednodušenou metodou v klauzuli 8.4.3.3 [1]. Toto aplikované zatížení je rovné 0,005krát celkové faktorované zatížení gravitačním na daném podlaží a mělo by být rozloženo podobně jako gravitační zatížení. Neúčetní zatížení jsou vždy aplikována ve směru, který generuje největší destabilizující efekt. To znamená, že tato zatížení by měla být aplikována ve stejném směru jako boční vítr, aby se generovaly nejvyšší deformace a vnitřní síly na konstrukci.
Příloha O.2 – Účinky stability v elastické analýze
Jako alternativu k výše uvedenému přístupu zjednodušené analýzy stability mohou inženýři využít Přílohu O.2 k uspokojení požadavků na stabilitu stanovených v klauzuli 8.4.1 [1]. Tento přístup byl přidán do normy 2019 a má mnoho podobností s americkým manuálem pro návrh oceli AISC 360-16 Ch. C Metoda přímé analýzy.
Geometrické nelinearity
Geometrické nelinearity, nebo efekty druhého řádu, jsou řešeny v O.2.2 [1]. Stejně jako zjednodušená metoda lze přímo provést analýzu druhého řádu, která zahrnuje účinky zatížení působících na odkloněné body průsečíků členů (efekty P-Δ). Navíc by se mělo zvážit, že zatížení osy působí na prohnutý tvar člena podél délky (P-δ). V O.2.2 [1] jsou uvedena ustanovení, kdy lze P-δ zcela zanedbat. Na druhou stranu, pokud je P-δ zahrnut přímo v analýze, může být faktor U1 nastaven na 1,0 použité v klauzuli 13.8 - Návrh členské komprese a ohybu [1].
Geometrické imperfece
Členské geometrické imperfece, jako je odchylka člena, nebo místní geometrické imperfece, jako je odchylka prvku, které jsou pro členy, není třeba zvažovat při navrhování podle klauzule O.2 [1]. Nicméně, globální geometrické imperfece by měly být zváženy přímým modelováním nebo použitím neúčetních bočních zatížení. Existuje výjimka, že tyto globální geometrické imperfece mohou být zanedbány pro boční zatížení, pouze pokud splňují požadavky stanovené v klauzuli O.2.3.1 [1]. Mezi požadavky patří, že gravitační zatížení konstrukce jsou primárně podpírána vertikálními konstrukčními prvky a že poměr mezi maximálním posunem podlaží druhého řádu a posunem podlaží prvního řádu s použitím snížené tuhosti člena podle klauzule O.2.4 [1] nepřesáhne 1,7 na žádné úrovni podlaží.
Když inženýr nemůže tyto imperfece zanedbat, může být použit první způsob přímého modelování. Průsečíkové body člena by měly být posunuty z jejich původních míst. Amplituda tohoto počátečního posunu je stanovena v klauzuli 29.3 [1] a aplikována v největším destabilizujícím směru, který je u většiny budov tolerancí 1/500 pro odklonění sloupů. Významným problémem této metody je velký počet scénářů modelu, které musí být zváženy. Teoreticky je potřeba čtyř posunů ve čtyřech různých směrech na každé úrovni podlaží. Pokud se přidají účinky odchylek člena s odkloněním sloupů, přidá to mnohem více scénářů modelování, které je třeba zvážit, aby se dosáhlo největšího destabilizujícího efektu.
Alternativní a preferovanou metodou pro globální geometrické imperfece je použití neúčetních bočních zatížení. Tato metoda je povolena, pouze pokud jsou gravitační zatížení primárně podpírána vertikálními konstrukčními prvky. Neúčetní boční zatížení byly pokryty dříve v tomto článku a jsou použitelná stejným způsobem jako ve zjednodušené analýze stability v klauzuli 8.4.3.2 [1]. Nicméně amplituda je snížena z 0,005 na 0,002krát faktorované gravitační zatížení na daném podlaží. Snížení velikosti je povoleno v klauzuli O.2.3.3, protože tato neúčetní zatížení zohledňují pouze globální geometrické imperfece, zatímco neúčetní zatížení v klauzuli 8.4.3.2 [1] také zohledňují efekty neelasticity a dalších nejistot.
Efekty neelasticity
Aby se zohlednily efekty neelasticity a také zvážily počáteční členské nebo místní geometrické imperfece a nejistoty v tuhosti a pevnosti, měly by být aplikovány snížené členské axiální a ohybové tuhosti podle následujících rovnic v klauzuli O.2.4 [1] na členy přispívající k boční stabilitě.
- EAr = 0,8τbEA
- EIr = 0,8τbEI
kde
- Cf/Cy < 0,5 ; τb = 1,0
- Cf/Cy > 0,5 ; τb = 4Cf/Cy(1-Cf/Cy)
Aby se zabránilo lokalizovaným deformacím, norma navrhuje aplikovat toto snížení tuhosti na všechny členy. Dále, když střihová tuhost (GA) a torzní tuhost (GJ) přispívají významně k boční stabilitě, mělo by se zvážit snížení tuhosti. Redukce tuhosti by neměla být použita při analýze náklonů, deformací, vibrací nebo přirozených vibrací.
Aplikace Přílohy O.2 v RFEM 6
Nová generace FEA program RFEM 6 zahrnuje nejnovější požadavky na stabilitu podle normy CSA S16:19 podle ustanovení Přílohy O.2.
Geometrické nelinearity
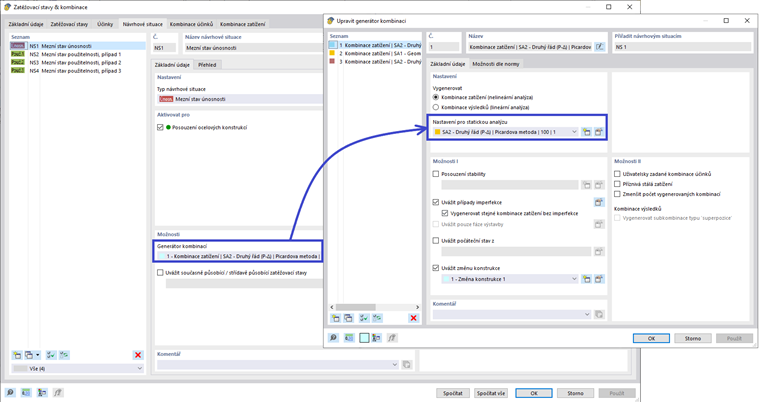
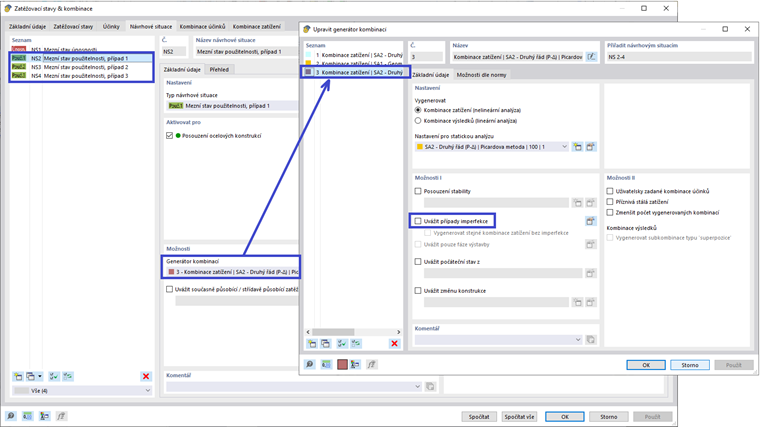
Efekty druhého řádu stanovené v klauzuli O.2.2 [1] jsou přímo zvažovány, když je metoda výpočtu statické analýzy nastavena na „Druhý řád (P-Δ)“. To lze aplikovat v možnostech Průvodce Kombinacemi Design Situace. Poté budou všechny zatížovací kombinace pod Design Situací automaticky nastaveny na analýzu druhého řádu. Uživatel má možnost individuálně upravit nastavení statické analýzy zatížovací kombinace, pokud preferuje.
Nejen, že jsou zahrnuty efekty P-Δ pro analýzu členů, ale také jsou automaticky zvažovány P-δ. Pro více informací o tomto tématu a ověření v RFEM 6 se podívejte na: Databáze znalostí 1759 .
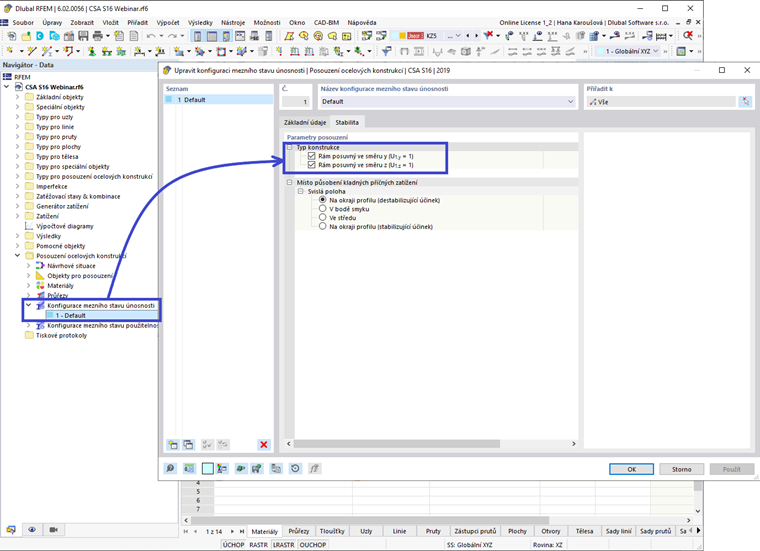
Proto může být faktor U1 nastaven na 1,0 specifikovaný v klauzuli 13.8 pro návrh ocelových členů. Tato volba se nachází v doplňku Navrhování oceli – Konečné konfigurace – Stabilita – Návrhové parametry.
Geometrické imperfece
Uživatel RFEM 6 má možnost přímo modelovat globální geometrické imperfece tím, že posune body nebo uzly průsečíků členů. Nicméně, aby se zajistilo, že tato metoda vytváří největší destabilizující efekt, bude potřeba provést více modelů s různými scénáři. Toto je časově náročné a těžkopádné.
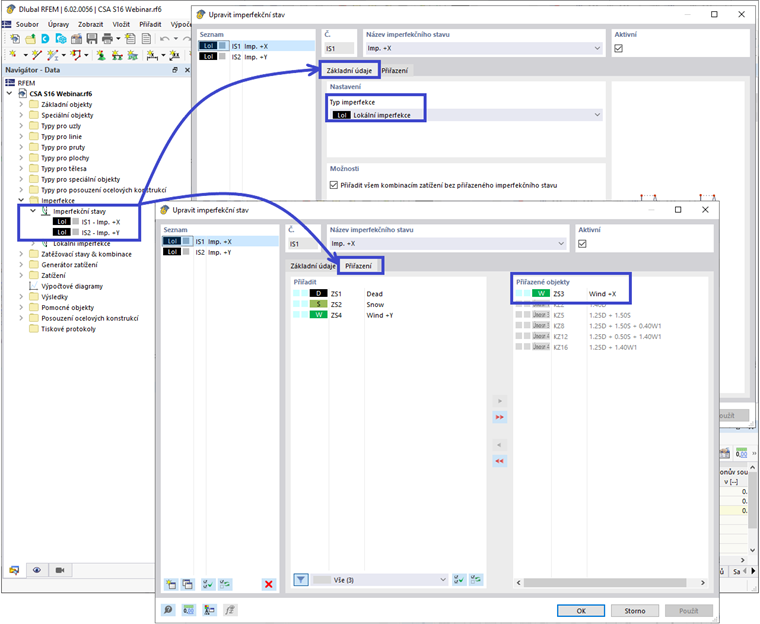
Alternativním přístupem je přibližně použít neúčetní zatížení pomocí možností imperfekce poskytnutých v RFEM 6. Nejprve musí být definovány případy imperfekce s typem imperfekce nastaveným na „Lokální imperfekce“ pod záložkou Hlavní. Ty by obvykle zahrnovaly případy ve ortogonálních směrech X a Y, v závislosti na aplikaci bočních zatížení, jako je vítr a seizmické zatížení. Případ imperfekce může být poté přiřazen pod záložkou Přiřazení ke specifickým zatěžovacím případům, aby se dosáhl největšího destabilizujícího efektu (například neúčetní zatížení ve směru +X by mělo být použito pouze s větrem v směru +X).
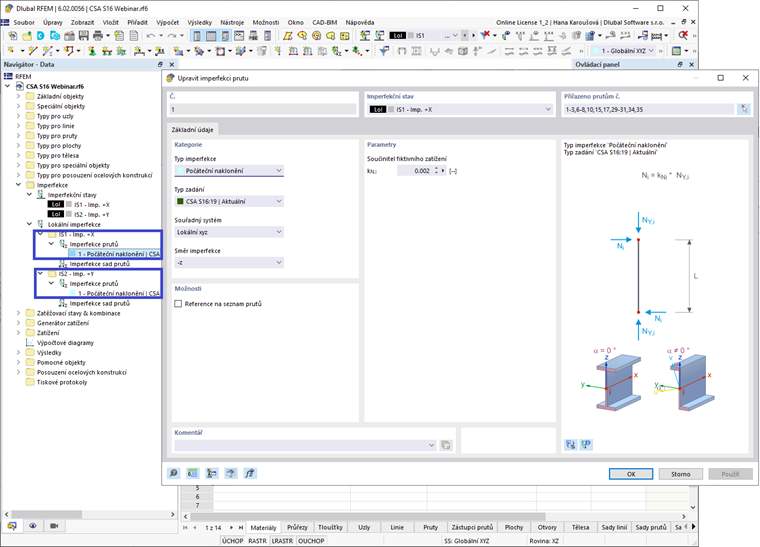
Po vygenerování Případů imperfekce mohou být členové imperfekcí definovány. Dialogové okno Členské imperfekce obsahuje CSA S16:19 v rozbalovacích možnostech. Neúčetní zatížení se aplikuje na konec člena (např. vrchol sloupu) s velikostí rovnou 0,002 (nebo 0,005, pokud používáte zjednodušenou metodu stability) násobené axiální silou člena (použité zatížení členů). Na opačný konec člena se shodně aplikuje síla, aby se zabránilo nerealistickým základním smykovým silám. Definice imperfekce se aplikuje na lokální osy členů ve stejném směru jako aplikované boční zatížení, jako je vítr nebo seizmické zatížení. Definice se dále aplikuje na všechny vertikální členy v modelu.
Po aplikaci imperfekcí na model je Design Situace ve výchozím nastavení nastavena tak, aby zohledňovala imperfekce pro všechny zatěžovací kombinace. Imperfekce by měly být aplikovány na Konečné návrhové situace, ale vypnuty pro Situace návrhu použitelnosti. To lze nastavit vytvořením nového typu definice Průvodce Kombinacemi, vypnutím možností zohlednění imperfekce a použitím pouze na Situace návrhu použitelnosti.
Efekty neelasticity
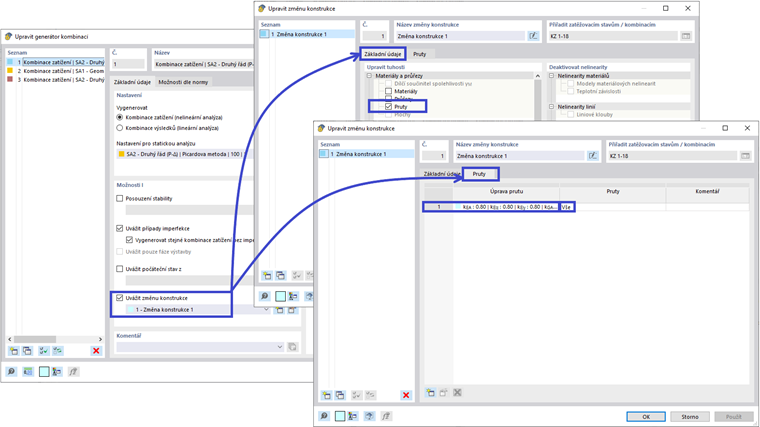
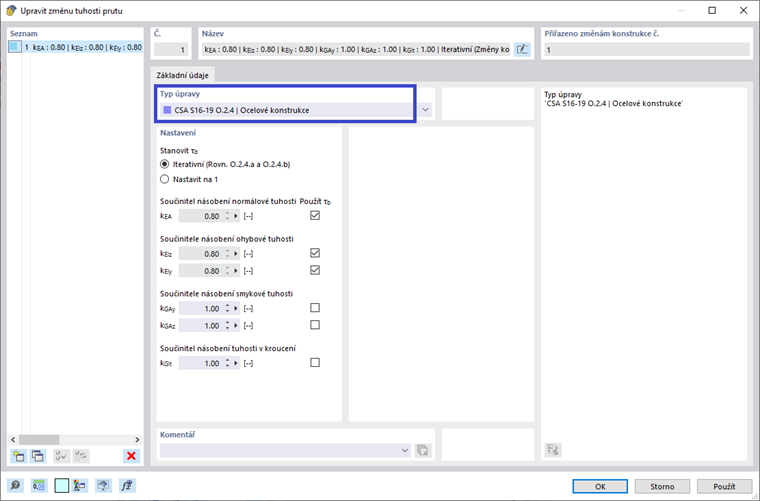
Redukce tuhostí se použijí pouze na Konečnou návrhovou situaci, opět prostřednictvím možností definice Průvodce Kombinacemi a zaškrtávacího políčka „Zvážit úpravu struktury“. Může být vytvořena nová definice úpravy struktury. Zaškrtávací políčko „Členové“ je vybráno pod záložkou Hlavní - Materiály a sekce. Tím se otevře nová záložka Členové, kde je definována úprava tuhosti členů podle CSA S1-19 O.2.4 | Ocelové konstrukce. Tento typ definice umožňuje programu buď automaticky vypočítat redukční faktor τb, nebo může být pro všechny členy nastavena obecná hodnota 1,0. Navíc, faktor 0.8 může být aplikován na různé typy tuhosti členů. Uživatel může určit, zda by se faktor τb a 0.8 měl aplikovat pouze na axiální a ohybovou tuhost člena, nebo zda by měla být zvážena také střihová a torzní tuhost. Po zadání vlastností úpravy tuhosti může být definice použita pro specifické členy nebo může být nastaven termín "Vše", aby se aplikoval pro všechny členy v modelu.
Protože redukce tuhosti členů by neměla být zvášena při návrhu použitelnosti (například, kontrolách průhybu), mělo by zaškrtávací políčko „Zvážit úpravu struktury“ zůstat nezaškrtnuté pro definici Průvodce Kombinacemi pro Situace návrhu použitelnosti.
Po těchto úpravách budou všechny faktorované zatěžovací kombinace zahrnovat úpravu tuhosti konstrukce, zatímco všechny nepodmíněné zatěžovací kombinace budou používat plnou tuhost členů.
Shrnutí
Významné požadavky na návrh stability podle Přílohy O.2 v kanadském manuálu pro návrh oceli CSA S16:19 jsou plně začleněny do pracovního postupu analýzy RFEM 6. Nejpozoruhodněji tyto požadavky zahrnují analýzu druhého řádu, schopnost zvažovat neúčetní zatížení jako imperfekce, stejně jako snížené tuhosti členů. Pro detailní ukázku tohoto tématu se podívejte na webinář: Posouzení ocelových konstrukcí podle CSA S16:19 v programu RFEM 6 (USA) .