Устойчивость конструкции не является новым явлением, когда речь идет о проектировании стальных конструкций. Канадский стандарт проектирования стали CSA S16 и его последнее издание 2019 года не являются исключением. Подробные требования к устойчивости могут быть решены либо с помощью упрощенного метода анализа устойчивости в пункте 8.4.3, либо, впервые для стандарта 2019 года, методом учёта эффектов устойчивости в упругом анализе, представленным в Приложении O [1].
Пункт 8.4.1 [1] перечисляет требования к устойчивости, которые проектирование конструкции должно учитывать с использованием любого из методов. Это включает в себя деформации, влияющие на структуру, эффекты второго порядка, включая P-Δ и P-δ, глобальные и элементные геометрические несовершенства, уменьшение жесткости с учётом уступок элементов и остаточных напряжений, и, наконец, неопределённости в жесткости и прочности конструкции.
Пункт 8.4.3 – Упрощенный метод анализа устойчивости
Согласно упрощенному методу анализа устойчивости, указанному в 8.4.3 [1], перечислены лишь несколько требований.
Геометрические нелинейности
Во-первых, учитываются эффекты второго порядка элементов, или P-Δ, которые могут быть непосредственно учтены в анализе. Метод расчета анализа второго порядка наиболее распространен во многих программах для анализа структуры сегодня. Альтернативой является усиление всех осевых нагрузок и моментов изгиба элементов, полученных из анализа первого порядка, фактором U2, определенным в 8.4.3.2(b) [1]. Этот подход может быть более подходящим для ручных расчетов или если программное обеспечение для анализа структуры не включает автоматически эффекты P-Δ.
Геометрические несовершенства
Условные поперечные нагрузки являются вторым пунктом, перечисленным в упрощенном методе в пункте 8.4.3.3 [1]. Эта приложенная нагрузка равна 0.005 от общей функториальной гравитационной нагрузки на рассматриваемом уровне и должна распределяться аналогично гравитационной нагрузке. Условные нагрузки всегда прикладываются в направлении, которое создаёт наибольший дестабилизирующий эффект. Это означает, что такие нагрузки должны прикладываться в том же направлении, что и боковая ветровая нагрузка, чтобы вызвать наибольшие деформации и внутренние силы в конструкции.
Приложение O.2 – Эффекты устойчивости в упругом анализе
Как альтернатива упрощенному подходу анализа устойчивости, инженеры могут использовать Приложение O.2 для завершения требований устойчивости, установленных в пункте 8.4.1 [1]. Этот подход был добавлен в стандарт 2019 года и имеет много сходств с американским руководством по проектированию стали AISC 360-16 Ch. C Метод прямого анализа.
Геометрические нелинейности
Геометрические нелинейности, или эффекты второго порядка, рассматриваются в O.2.2 [1]. Подобно упрощенному методу, анализ второго порядка можно выполнить непосредственно, включая эффекты нагрузок, действующих в точках смещений элементов (эффекты P-Δ). Дополнительно, следует учитывать эффекты осевых нагрузок, действующих на дефлекционную форму элемента вдоль его длины (P-δ). Существуют положения, приведенные в O.2.2 [1], где P-δ можно полностью не учитывать. С другой стороны, если P-δ включен непосредственно в анализ, фактор U1 можно установить равным 1.0, указанным в п. 13.8 - Проектирование элементов сжатия и изгиба [1].
Геометрические несовершенства
Геометрические несовершенства элементов, такие как отклонение элементов от прямолинейности или локальные геометрические несовершенства, такие как отклонение элементов от прямолинейности для всех членов, не нужно учитывать при проектировании по пункту O.2 [1]. Однако глобальные геометрические несовершенства следует учитывать с помощью прямого моделирования или использования условных боковых нагрузок. Существует исключение, что эти глобальные геометрические несовершенства можно не учитывать для комбинаций боковых нагрузок, только если они соответствуют требованиям, изложенным в пункте O.2.3.1 [1]. Среди требований – чтобы гравитационные нагрузки конструкции поддерживались преимущественно вертикальными структурными элементами, и чтобы отношение между максимальным перемещением этажа второго порядка и перемещением этажа первого порядка с использованием уменьшенной жесткости элементов согласно пункту O.2.4 [1] не превышало 1.7 на любом уровне этажа.
Когда инженер не может не учитывать эти несовершенства, можно использовать первый метод прямого моделирования. Пересекающиеся точки элементов должны быть смещены от их первоначальных местоположений. Амплитуда этого начального смещения изложена в пункте 29.3 [1] и прикладывается в наиболее дестабилизирующем направлении, которое для большинства строительных конструкций является допуском 1/500 на уклон колонны. Значительная проблема с этим методом заключается в большом количестве сценариев моделей, которые необходимо учитывать. Теоретически, четыре смещения необходимы в четырех разных направлениях на каждом уровне этажа. Если эффекты отклонения элементов от прямолинейности также сочетаются с наклоном колонн, это добавляет много дополнительных сценариев моделирования, которые необходимо рассмотреть для достижения наибольшего дестабилизирующего эффекта.
Альтернативным и предпочтительным методом для глобальных геометрических несовершенств является применение условных боковых нагрузок. Этот метод разрешен только тогда, когда гравитационные нагрузки поддерживаются преимущественно вертикальными структурными элементами. Условные боковые нагрузки были описаны ранее в этой статье и применяются так же, как и упрощенный анализ устойчивости в пункте 8.4.3.2 [1]. Однако амплитуда уменьшена с 0.005 до 0.002 от фактической гравитационной нагрузки на соответствующем уровне. Уменьшение величины разрешено в пункте O.2.3.3, так как эти условные нагрузки учитывают только глобальные геометрические несовершенства, тогда как условные нагрузки в пункте 8.4.3.2 [1] также учитывают эффекты неупругости и другие неопределенности.
Эффекты неупругости
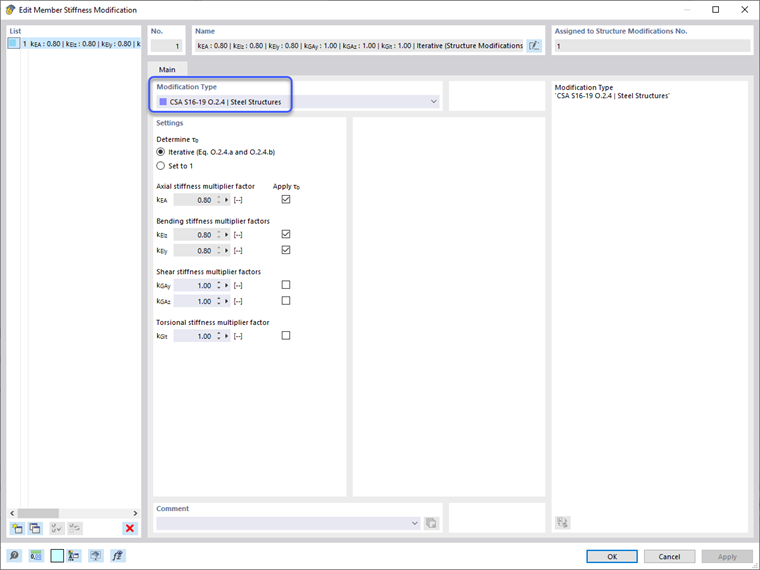
Для учета эффектов неупругости и также учета начальных несовершенств элементов или локальных геометрических несовершенств, а также неопределенности в жесткости и прочности, снижение осевой и изгибной жесткости элементов в соответствии с следующими уравнениями в пункте O.2.4 [1] должно применяться к элементам, способствующим боковой устойчивости.
- EAr = 0.8τbEA
- EIr = 0.8τbEI
где
- Cf/Cy < 0.5 ; τb = 1.0
- Cf/Cy > 0.5 ; τb = 4Cf/Cy(1-Cf/Cy)
Чтобы избежать локальных искажений, стандарт предлагает применять это снижение жесткости ко всем элементам. Более того, когда жесткость на сдвиг (GA) и крутильная жесткость (GJ) значительно способствуют боковой устойчивости, следует учитывать снижение жесткости. Снижение жесткости не следует использовать при анализе наклонов, прогибов, вибраций или естественных вибраций.
Приложение O.2 в использовании в RFEM 6
Новое поколение программы конечно-элементного анализа RFEM 6 включает последние требования к устойчивости стандарта CSA S16:19 согласно положениям Приложения O.2.
Геометрические нелинейности
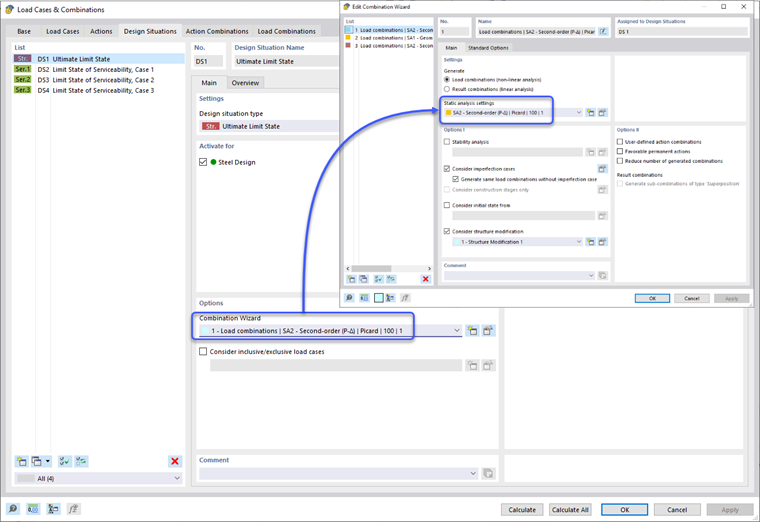
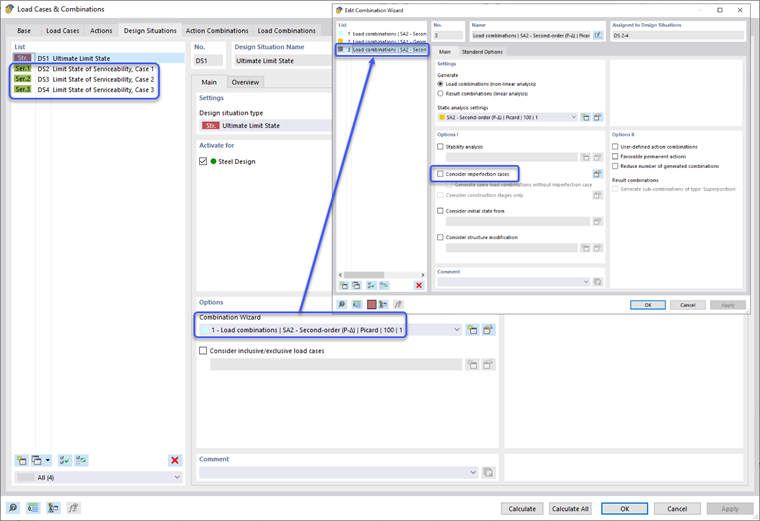
Эффекты второго порядка, изложенные в пункте O.2.2 [1], учитываются непосредственно, когда метод расчета статического анализа установлен на "Второго порядка (P-Δ)". Это может быть применено в опциях Мастера комбинации проектных ситуаций. В свою очередь, все комбинации нагрузок в проектной ситуации автоматически устанавливаются для анализа второго порядка. Пользователь имеет возможность индивидуально изменить настройки статического анализа комбинации нагрузок, если предпочитает.
Не только эффекты P-Δ включены для анализа элементов, но и P-δ также автоматически учитывается. Для получения дополнительной информации по этой теме и подтверждения в RFEM 6, взгляните на: База знаний 1759 .
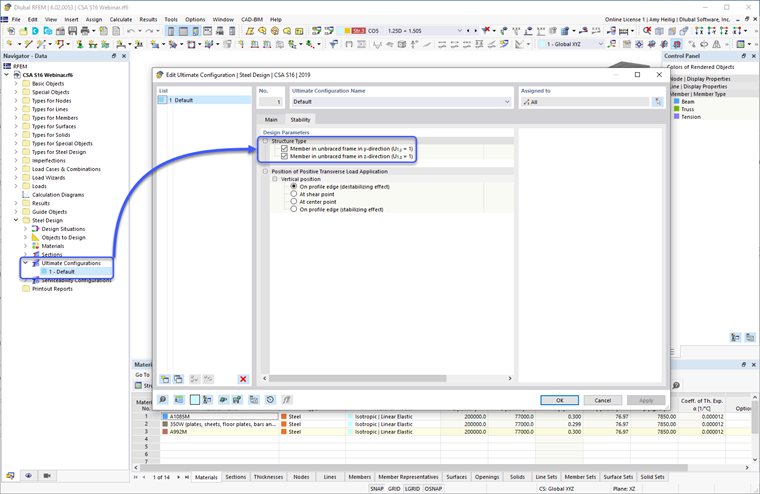
Поэтому фактор U1 можно установить равным 1.0, как указано в пункте 13.8 для проектирования стальных элементов. Эта опция находится в надстройке Стальное проектирование – Окончательные конфигурации – Устойчивость – Параметры проектирования.
Геометрические несовершенства
Пользователь RFEM 6 имеет возможность напрямую моделировать глобальные геометрические несовершенства, смещая точки или узлы пересечения элементов. Однако, чтобы убедиться, что этот метод создаёт наибольший дестабилизирующий эффект, потребуется выполнение множества моделей с различными сценариями. Это довольно трудоемко и обременительно.
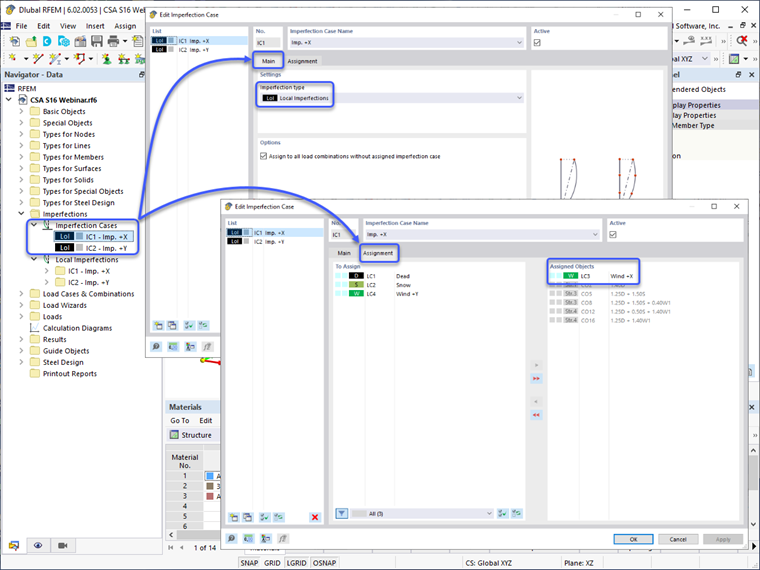
Альтернативный подход – применить относительные нагрузки с опциями несовершенства, предоставляемыми в RFEM 6. Для начала необходимо сначала определить Случаи несидеальности с типом несидеальности, установленным на "Местные несовершенства" на главной вкладке. Обычно это включало бы случаи в ортогональных направлениях X и Y, в зависимости от применения боковых нагрузок, таких как ветер и сейсмика. Затем Случай несовершенства может быть соотнесен на вкладке Назначения с конкретными случаями нагрузок для создания наибольшего дестабилизирующего эффекта (например, относительные нагрузки в направлении +X должны применяться только вместе с ветровыми нагрузками в направлении +X).
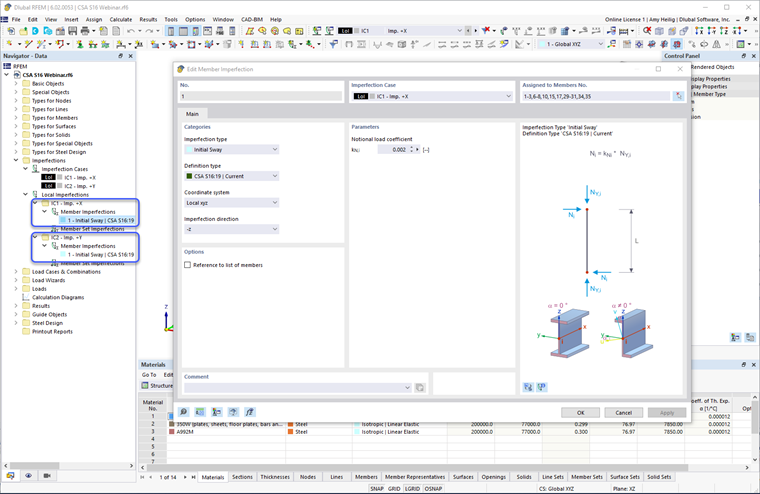
После создания Случаев несидеальности могут быть определены несовершенства элемента. Диалоговое окно Несидеальности элемента включает CSA S16:19 в выпадающих опциях. Относительная нагрузка прикладывается к концу элемента (т.е. верхушке колонны) с величиной, равной 0.002 (или 0.005, если используется упрощенный метод устойчивости), умноженной на осевую силу элемента (приложенную гравитационную нагрузку на элемент). Противоположная и равная сила внутренне прикладывается к противоположному концу элемента для избежания нереалистичных основательных сдвигов. Определение несовершенства применяется к локальным осям элементов в том же направлении, что и приложенная боковая нагрузка, такая как ветер или сейсмическая. Определение дополнительно применяется ко всем вертикальным элементам в модели.
После применения несовершенств к модели Проектная ситуация устанавливается по умолчанию для учета несовершенств для всех комбинаций нагрузок. Несовершенства должны применяться к Проектным ситуациям окончательных расчетов, но быть выключены для Проектных ситуаций эксплуатационных расчетов. Это можно установить, создав новый тип определения Мастера комбинации, выключив опции учета несовершенств и применив только к Проектным ситуациям эксплуатационных расчетов.
Эффекты неупругости
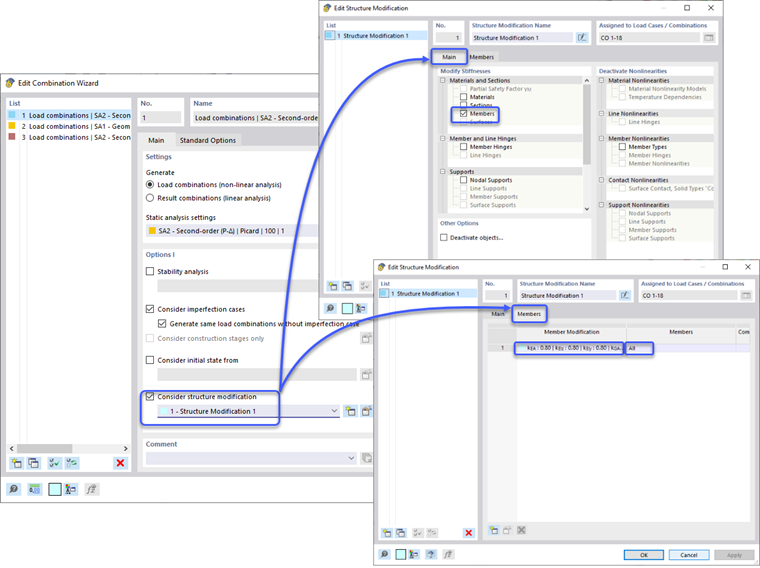
Снижения жесткости применяются к Проектной ситуации окончательных расчетов только через опции определения Мастера комбинации и флажок "Учесть модификацию структуры". Можно создать новое определение модификации структуры. Флажок "Элементы" выбран на главной вкладке - Материалы и Сечения. Это вызывает новую вкладку Элементы, где определяется Модификация жесткости элемента согласно CSA S1-19 O.2.4 | Стальные конструкции. Этот тип определения позволяет программе либо автоматически рассчитывать коэффициент снижения τb, либо установить обобщенное значение 1.0 для всех элементов. Дополнительно, фактор 0.8 может быть применен к различным типам жесткости элемента. Пользователь может определить, следует ли применять τb и фактор 0.8 только к осевой и изгибной жесткости элемента или также учитывать жесткость на сдвиг и кручение. После ввода свойств модификации жесткости определение можно применить к конкретным элементам, или можно установить термин "Все" для применения ко всем элементам в модели.
Поскольку снижение жесткости элемента не следует учитывать для проектирования эксплуатации (например, проверки прогибов), флажок "Учесть модификацию структуры" должен оставаться не отмеченным для определения Мастера комбинации Проектных ситуаций эксплуатационных расчетов.
После этих изменений все полные комбинации нагрузок будут включать снижение жесткости модификации структуры, в то время как все неполные комбинации нагрузок будут использовать полную жесткость элементов.
Резюме
Значительные требования к проектированию устойчивости согласно Приложению O.2 в канадском руководстве по проектированию Stali CSA S16:19 полностью интегрированы в процесс анализа в RFEM 6. Наиболее заметно, эти требования включают анализ второго порядка, возможность учета относительных нагрузок как несовершенств, а также уменьшение жесткости элементов. Чтобы увидеть эту тему продемонстрированной в подробном видео-примере, ознакомьтесь с вебинаром: Расчет стальных конструкций по норме CSA S16:19 в программе RFEM 6 (США) .