Stabilność konstrukcji nie jest nowym zjawiskiem w odniesieniu do projektowania stali. Kanadyjski standard projektowania stali CSA S16, a najnowsze wydanie z 2019 roku nie jest wyjątkiem. Szczegółowe wymagania dotyczące stabilności można uwzględnić za pomocą uproszczonej metody analizy stabilności w klauzuli 8.4.3 lub, nowość w standardzie z 2019 roku, metody skutków stabilności w analizie sprężystej zdefiniowanej w załączniku O [1].
Klauzula 8.4.1 [1] wymienia wymagania dotyczące stabilności, które projekt konstrukcyjny powinien uwzględniać korzystając z jednej z metod. Obejmują one deformacje przyczyniające się do konstrukcji, efekty drugiego rzędu, w tym P-Δ i P-δ, globalne i lokalne niedoskonałości geometryczne, redukcję sztywności uwzględniającą uplastycznianie się członów i naprężenia resztkowe, a na końcu niepewność w zakresie sztywności i wytrzymałości konstrukcji.
Klauzula 8.4.3 – Uproszczona metoda analizy stabilności
W ramach uproszczonej metody analizy stabilności podanej w 8.4.3 [1] wymieniono tylko kilka wymagań.
Nieliniowości geometryczne
Pierwszym z nich są efekty drugiego rzędu dla członów, czyli P-Δ, które można bezpośrednio uwzględnić w analizie. Metoda obliczeniowa analizy drugiego rzędu jest dziś najczęściej stosowana w wielu programach do analizy konstrukcyjnej. Alternatywą jest amplifykacja wszystkich obciążeń osiowych członów i momentów zginających uzyskanych z analizy pierwszego rzędu przez współczynnik U2 zdefiniowany w 8.4.3.2(b) [1]. Podejście to może być lepiej dostosowane do obliczeń ręcznych lub gdy oprogramowanie do analizy konstrukcyjnej nie obejmuje automatycznie efektów P-Δ.
Niedoskonałości geometryczne
Obciążenia teoretyczne boczne to drugi element wymieniony w ramach uproszczonej metody w klauzuli 8.4.3.3 [1]. To zastosowane obciążenie jest równe 0,005-krotności całkowitego obciążenia grawitacyjnego, faktoryzowanego na rozważanym piętrze, i powinno być rozproszone podobnie jak obciążenie grawitacyjne. Obciążenia teoretyczne są zawsze stosowane w kierunku, który generuje największy efekt destabilizujący. Oznacza to, że takie obciążenia powinny być stosowane w tym samym kierunku co obciążenie wiatrem bocznym, aby wygenerować największe deformacje i siły wewnętrzne w konstrukcji.
Załącznik O.2 – Skutki stabilności w analizie sprężystej
Jako alternatywa dla powyższego uproszczonego podejścia do analizy stabilności, inżynierowie mogą wykorzystać załącznik O.2, aby spełnić wymagania dotyczące stabilności określone w klauzuli 8.4.1 [1]. Podejście to zostało dodane do standardu z 2019 roku i ma wiele podobieństw do amerykańskiego podręcznika projektowania stali AISC 360-16 Ch. C Metoda analizy bezpośredniej.
Nieliniowości geometryczne
Nieliniowości geometryczne, lub efekty drugiego rzędu, są uwzględnione w O.2.2 [1]. Podobnie jak w przypadku uproszczonej metody, można bezpośrednio przeprowadzić analizę drugiego rzędu, która uwzględnia efekty obciążeń działających w przesuniętych punktach przecięć członów (efekty P-Δ). Dodatkowo, należy uwzględnić efekty obciążeń osiowych działających na przegięty kształt członu wzdłuż jego długości (P-δ). Istnieją przepisy podane w O.2.2 [1], gdzie P-δ można całkowicie pominąć. Z drugiej strony, jeśli P-δ jest bezpośrednio uwzględnione w analizie, to współczynnik U1 można ustawić na 1,0 używany w klauzuli 13.8 – projektowanie członu osiowego i zginającego [1].
Niedoskonałości geometryczne
Niedoskonałości geometryczne członów, takie jak ich nieprostoliniowość, lub lokalne niedoskonałości geometryczne, takie jak nieprostoliniowość elementów członów, nie muszą być uwzględniane podczas projektowania zgodnie z klauzulą O.2 [1]. Jednak globalne niedoskonałości geometryczne powinny zostać uwzględnione z bezpośrednim modelowaniem lub z wykorzystaniem obciążeń teoretycznych bocznych. Istnieje jednak wyjątek, że globalne niedoskonałości geometryczne można zlekceważyć dla kombinacji obciążeń bocznych tylko wtedy, gdy spełniają wymogi określone w klauzuli O.2.3.1 [1]. Wśród wymagań znajduje się to, że grawitacyjne obciążenia konstrukcji są podtrzymywane głównie przez pionowe elementy strukturalne i to, że proporcje pomiędzy maksymalnym przemieszczeniem piętra drugiego rzędu a pierwszego rzędu, przy użyciu zmniejszonej sztywności członów zgodnie z klauzulą O.2.4 [1], nie przekracza 1.7 na żadnym poziomie piętra.
Kiedy inżynier nie może zignorować tych niedoskonałości, można zastosować pierwszą metodę bezpośredniego modelowania. Punkty przecięcia członów powinny być przesunięte z ich oryginalnych lokalizacji. Amplituda tego początkowego przesunięcia jest określona w klauzuli 29.3 [1] i stosowana w kierunku największego efektu destabilizującego, który dla większości struktur budowlanych wynosi 1/500 tolerancji dla niedostatecznego pionu kolumny. Znaczący problem z tą metodą to duża liczba scenariuszy modelowych, które muszą być rozważone. Teoretycznie, cztery przesunięcia są potrzebne w czterech różnych kierunkach na każdym poziomie piętra. Jeśli efekty nieprostoliniowości członów są również łączone z nachyleniem kolumny, to dodaje to wiele więcej scenariuszy modelowych do rozważenia, aby spełnić największy efekt destabilizujący.
Alternatywną i preferowaną metodą dla globalnych niedoskonałości geometrycznych jest zastosowanie obciążeń teoretycznych bocznych. Metoda ta jest dozwolona tylko wtedy, gdy grawitacyjne obciążenia są głównie podtrzymywane przez pionowe elementy strukturalne. Obciążenia teoretyczne boczne zostały omówione wcześniej w tym artykule i są stosowane w ten sam sposób jak uproszczona analiza stabilności w klauzuli 8.4.3.2 [1]. Jednak amplituda jest zmniejszona z 0,005 do 0,002 razy obciążenie grawitacyjne, faktoryzowane na odpowiednim piętrze. Zmniejszenie wielkości jest dozwolone w klauzuli O.2.3.3, ponieważ te obciążenia teoretyczne uwzględniają tylko globalne niedoskonałości geometryczne, podczas gdy obciążenia teoretyczne w klauzuli 8.4.3.2 [1] uwzględniają również efekt niesprężystośći i inne niepewności.
Efekty niesprężystości
Aby uwzględnić efekty niesprężystości oraz wziąć pod uwagę początkową niedoskonałość członów lub lokalne niedoskonałości geometryczne, a także niepewność co do sztywności i wytrzymałości, należy zastosować zmniejszoną sztywność osiową i zginającą członów zgodnie z następującymi równaniami w klauzuli O.2.4 [1] do członów przyczyniających się do stabilności bocznej.
- EAr = 0,8τbEA
- EIr = 0,8τbEI
gdzie
- Cf/Cy < 0,5 ; τb = 1,0
- Cf/Cy > 0,5 ; τb = 4Cf/Cy(1-Cf/Cy)
Aby uniknąć lokalnych deformacji, standard sugeruje zastosowanie tej redukcji sztywności do wszystkich członów. Dodatkowo, w przypadku, gdy sztywność ścinania (GA) i sztywność skrętna (GJ) znacząco wpływają na stabilność boczną, należy uwzględnić redukcję sztywności. Redukcja sztywności nie powinna być stosowana do analizy przemieszczeń, odkształceń, wibracji czy drgań naturalnych.
Zastosowanie załącznika O.2 w RFEM 6
Nowa generacja programu MES RFEM 6 zawiera najnowsze wymagania stabilności według standardu CSA S16:19 zgodnie z przepisami załącznika O.2.
Nieliniowości geometryczne
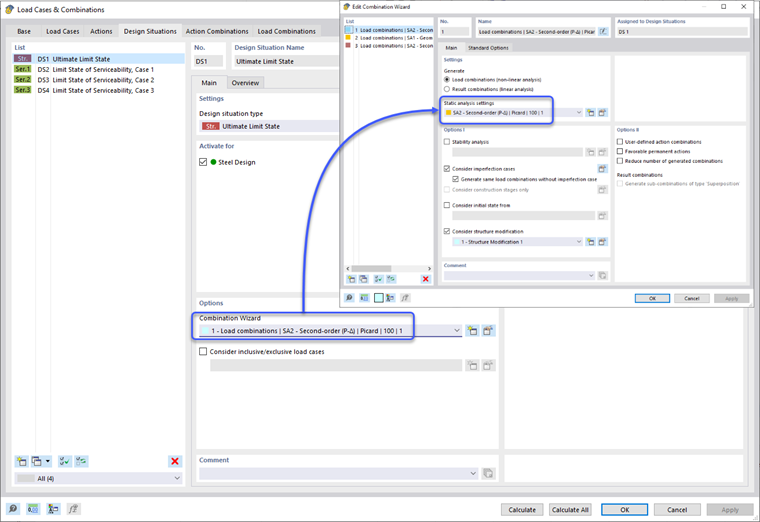
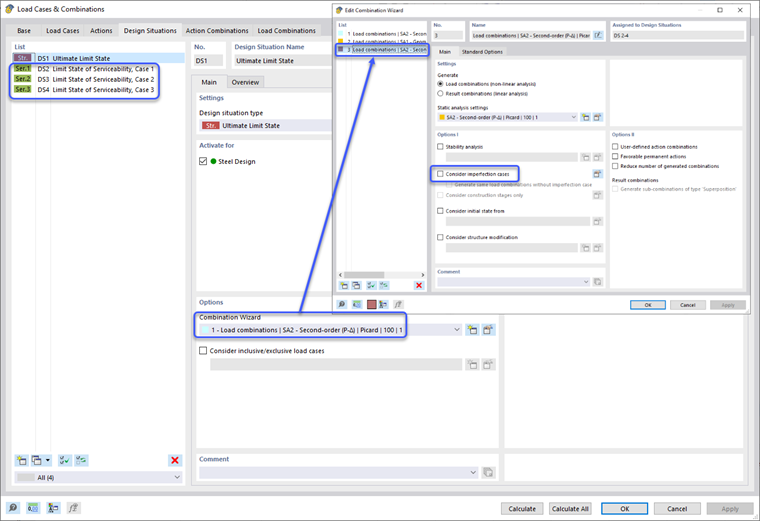
Efekty drugiego rzędu określone w klauzuli O.2.2 [1] są bezpośrednio uwzględniane, gdy metoda obliczeniowa analizy statycznej jest ustawiona na „Drugi rząd (P-Δ)”. Można to zastosować w opcjach Kreatora Kombinacji Syytuacji Projektowej. W rezultacie wszystkie kombinacje obciążeń pod Syytacją Projektową zostaną automatycznie ustawione również na analizę drugiego rzędu. Użytkownik ma możliwość indywidualnego modyfikowania ustawień analizy statycznej kombinacji obciążeń, jeśli takie jest jego preferencje.
Nie tylko efekty P-Δ są uwzględniane w analizie członu, ale także P-δ są automatycznie uwzględniane. Aby uzyskać więcej informacji na ten temat i zweryfikować w RFEM 6, zobacz: Baza informacji 1759 .
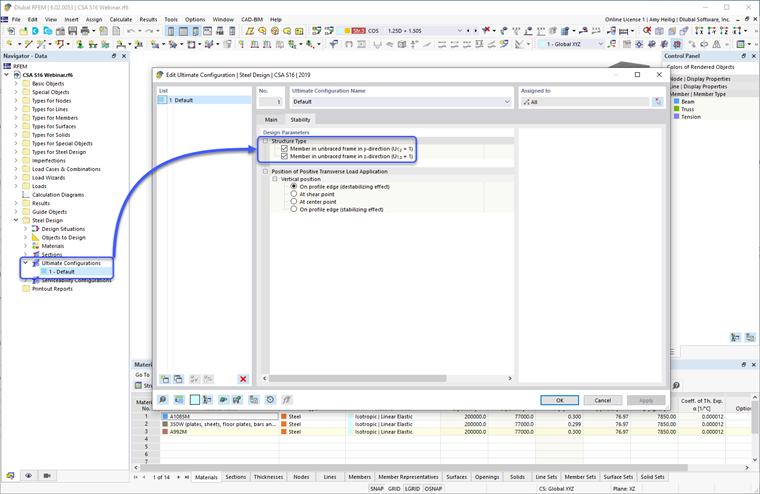
Dlatego współczynnik U1 można ustawić na 1,0 określony w klauzuli 13.8 dla projektowania członów stalowych. Ta opcja znajduje się w dodatku do projektowania stali – Konfiguracje ostateczne – Stabilność – Parametry projektowe.
Niedoskonałości geometryczne
Użytkownik RFEM 6 ma możliwość bezpośredniego modelowania globalnych niedoskonałości geometrycznych poprzez przemieszczenie punktów lub węzłów przecięcia członów. Jednak aby zapewnić, że ta metoda tworzy największy efekt destabilizujący, trzeba będzie przeprowadzić wiele modeli z różnymi scenariuszami. Jest to dość czasochłonne i uciążliwe.
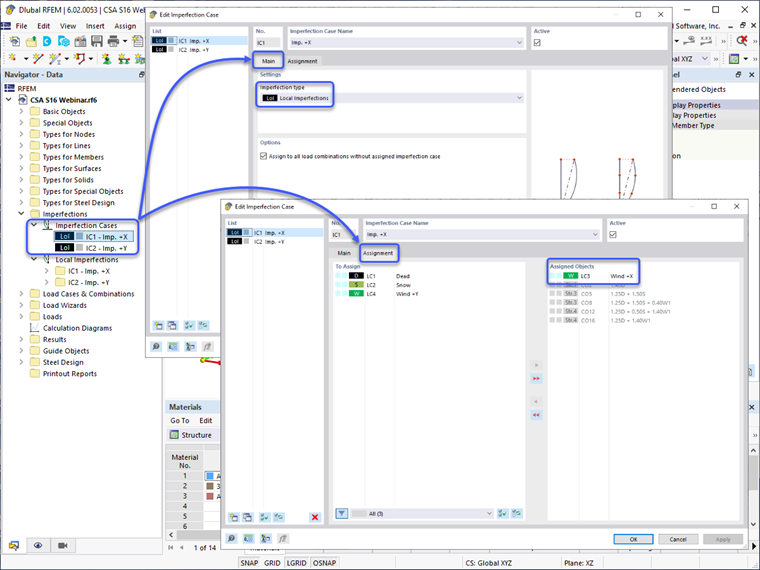
Podejściem alternatywnym jest zastosowanie obciążeń teoretycznych z opcjami niedoskonałości dostępnymi w RFEM 6. Na początek, należy zdefiniować przypadki niedoskonałości z typem niedoskonałości ustawionym na „Niedoskonałości lokalne” w zakładce głównej. Zwykle obejmują one przypadki w kierunkach ortogonalnych X i Y, w zależności od zastosowania obciążeń bocznych, takich jak wiatr i sejsmiczne. Przypadek Niedoskonałości można następnie skorelować w zakładce Przypisanie ze specyficznymi przypadkami obciążeń, aby wywołać największy efekt destabilizujący (na przykład obciążenia teoretyczne w kierunku +X powinny być stosowane tylko z obciążeniami wiatrowymi w kierunku +X).
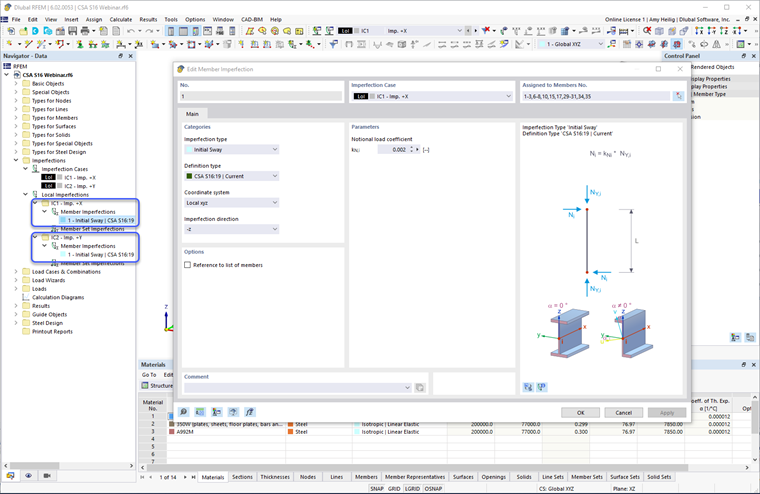
Po wygenerowaniu przypadków niedoskonałości można zdefiniować niedoskonałości członów. Okienko dialogowe Niedoskonałości Członów obejmuje opcje CSA S16:19 w menu rozwijanym. Obciążenie teoretyczne jest stosowane do końca członu (tj. szczytu kolumny) z wielkością równą 0,002 (lub 0,005, jeśli używa się uproszczonej metody stabilności) pomnożoną przez siłę osiową członu (obciążenie grawitacyjne członu). Równoważna i przeciwnie skierowana siła jest wewnętrznie stosowana na przeciwnym końcu członu, aby uniknąć nerealistycznych sił podstawowych. Definicja niedoskonałości jest stosowana do lokalnych osi członów w tym samym kierunku, co zastosowane obciążenie boczne, takie jak wiatr lub sejsmiczne. Definicja jest dalej stosowana do wszystkich członów pionowych w modelu.
Po zastosowaniu niedoskonałości do modelu, Syytuacja Projektowa jest domyślnie ustawiona, aby uwzględniać niedoskonałości dla wszystkich kombinacji obciążeń. Niedoskonałości powinny być stosowane do ostatecznych sytuacji projektowych, ale wyłączone dla sytuacji projektowych sprawdzających użyteczność. Można to ustawić, tworząc nową definicję typu Kreatora Kombinacji, wyłączając opcje rozważania niedoskonałości i stosując tylko do sytuacji projektowych sprawdzających użyteczność.
Efekty niesprężystości
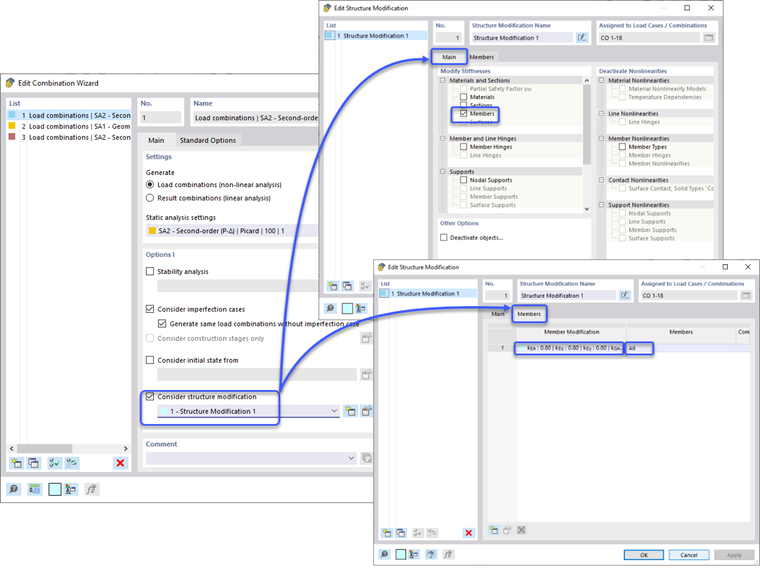
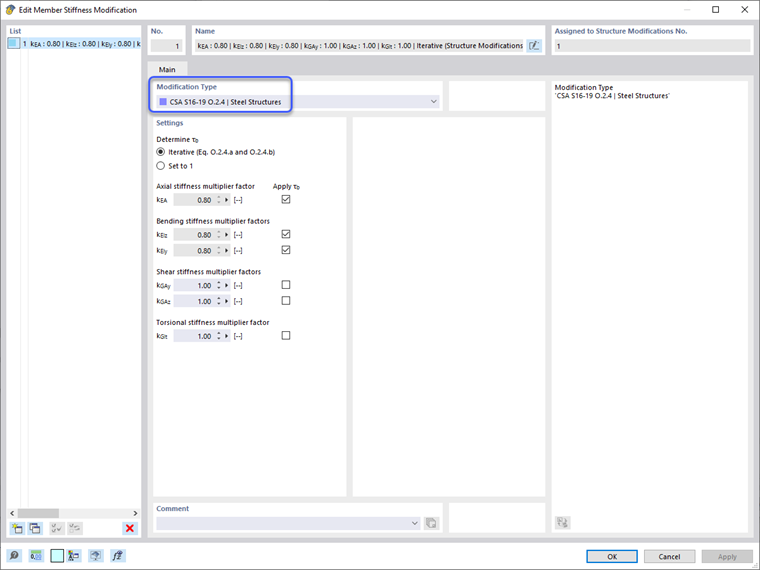
Redukcja sztywności jest stosowana tylko do ostatecznych sytuacji projektowych, ponownie poprzez opcje definicji Kreatora Kombinacji i zaznaczenie pola „Uwzględnij modyfikację struktury”. Można stworzyć nową definicję modyfikacji struktury. Pole wyboru „Członkowie” zostaje zaznaczone w zakładce głównej - Materiały i Przekroje. To otwiera nową zakładkę Członkowie, gdzie definicja Modyfikacji Sztywności Członów jest zdefiniowana zgodnie z CSA S1-19 O.2.4 | Konstrukcje stalowe. Ten typ definicji pozwala programowi obliczyć automatycznie współczynnik redukcji τb, lub wartość ogólną 1,0 można ustawić dla wszystkich członów. Dodatkowo, współczynnik 0,8 można zastosować do różnych typów sztywności członów. Użytkownik może zdecydować, czy współczynnik τb i 0,8 ma być stosowany tylko do osiowej i zginającej sztywności członów, czy także do sztywności ścinania i skrętnej. Po wprowadzeniu właściwości modyfikacji sztywności, definicję można zastosować do konkretnych członów lub ustawić termin „Wszystkie”, aby zastosować do wszystkich członów w modelu.
Ponieważ redukcja sztywności członów nie powinna być brana pod uwagę przy projektowaniu sprawdzającym użyteczność (na przykład przy sprawdzaniu odkształceń), pole „Uwzględnij modyfikację struktury” powinno pozostać niezaznaczone dla definicji Kreatora Kombinacji sytuacji projektowych sprawdzających użyteczność.
Po tych modyfikacjach wszystkie zafakturowane kombinacje obciążeń będą obejmować redukcję sztywności modyfikacji struktury, podczas gdy wszystkie nie zafakturowane kombinacje obciążeń będą korzystać z pełnej sztywności członów.
Podsumowanie
Znaczące wymagania projektowe dotyczące stabilności zgodnie z załącznikiem O.2 w kanadyjskim podręczniku projektowania stali CSA S16:19 są w pełni zintegrowane w przepływie pracy analizy RFEM 6. Najbardziej zauważalnie, te wymagania obejmują analizę drugiego rzędu, możliwość uwzględnienia obciążeń teoretycznych jako niedoskonałości, jak również zmniejszoną sztywność członów. Aby zobaczyć ten temat omówiony w szczegółowym przykładzie wideo, sprawdź webinar: CSA S16:19 Projektowanie konstrukcji stalowych w RFEM 6 (USA) .