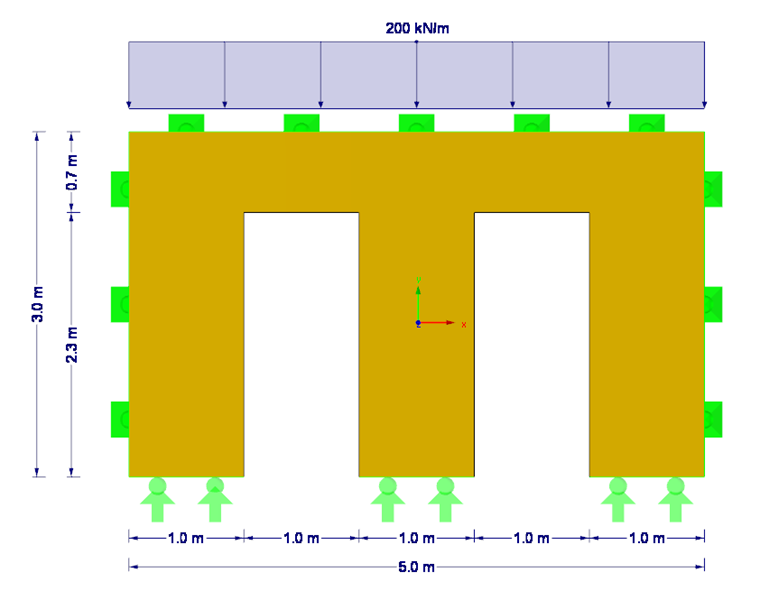
В нашем примере представлен расчет на потерю устойчивости при изгибе четырехугольной стены из поперечно-клееной древесины с двумя дверными проемами (см. рисунок 1). В данном случае определяющим случаем является сечение стены между воротами.
Расчет на потерю устойчивости при изгибе можно выполнить согласно [1] с методом эквивалентного стержня по главе 6.3.2 с внутренними силами по линейному статическому расчету или по разделу 5.4.4, с учетом несовершенств. В обоих случаях необходимо учитывать раздел 2.2.2. Для этого нужно применить средние значения параметров жесткости (модуль упругости и модуль сдвига), разделенные на частичный коэффициент надежности γM, для определения внутренних сил по методу второго порядка в соответствии с 2.4.1(2)P. Кроме того, [2] NCI NA.9.3.3 определяет те ситуации, когда расчет на устойчивость должен быть выполнен в соответствии с анализом второго порядка для плоских конструктивных элементов. Если уравнение NA.150 выполнено, то расчет на устойчивость можно выполнить с помощью расчета эквивалентных стержней и метода второго порядка. В противном случае расчеты должны быть выполнены исключительно по методу второго порядка.
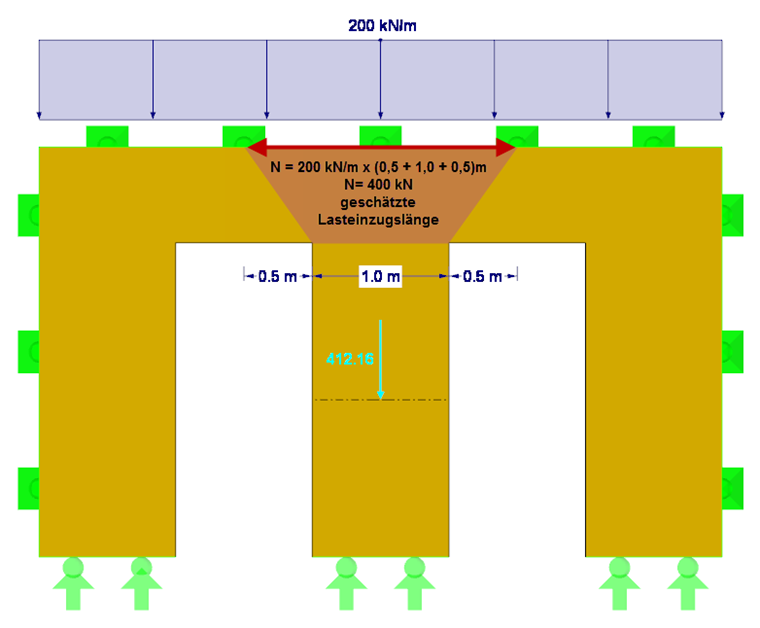
Сначала необходимо проверить, выполнено ли уравнение NA.150. Для этого нам потребуется значение действующей осевой силы Nd, жесткость на изгиб E∙I вдоль местной оси y, частный коэффициент надежности γM для поперечно-клееной древесины и полезная длина соответствующего профиля стены между воротами. Длина приложения нагрузки приблизительно равна 0,5 м + 1,0 м + 0,5 м = 2,0 м. Таким образом, результирующая сжимающая сила Nd равна 200 кН/м ∙ 2 м = 400 кН (без учета собственного веса). В качестве альтернативы, точное определение сжимающей силы с учетом собственного веса можно получить с помощью результирующих сил сечения в программе RFEM (см. рисунок 2). С учетом ортотропии и собственного веса сжимающая сила составляет 412 кН.
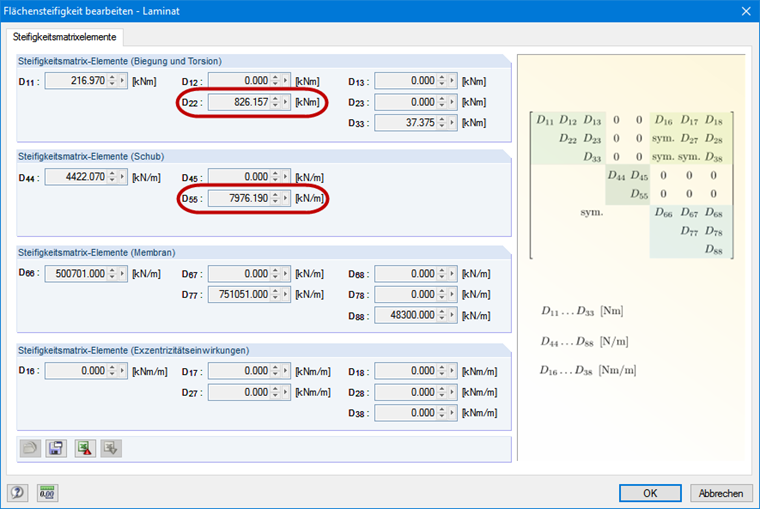
Жесткость на изгиб можно прямо вычесть из матрицы жесткости поверхности (см.рисунок 3). Для этого выберем поверхность стены от Stora Enso типа CLT CLT 100 C5s. Результирующая жесткость на изгиб в направлении y равна 826,16 кНм ∙ 1,0 м = 826,16 кНм².
Частичный коэффициент 1,3 применяется в соответствии с [2]. При определении расчетных длин у поперечно-клееной древесины необходимо также учесть жесткость на сдвиг в направлении y (см. рисунок 3). Коэффициент свободной длины β 1,0 применяется в соответствии со случаем Эйлера 2.
Критерий определения границ не выполнен 2,55 > 1,00; поэтому необходимо выполнить расчет устойчивости по методу второго порядка. И поскольку речь идет о расчете почти линейного стержня, в следующих статьях будет объяснено оба метода.
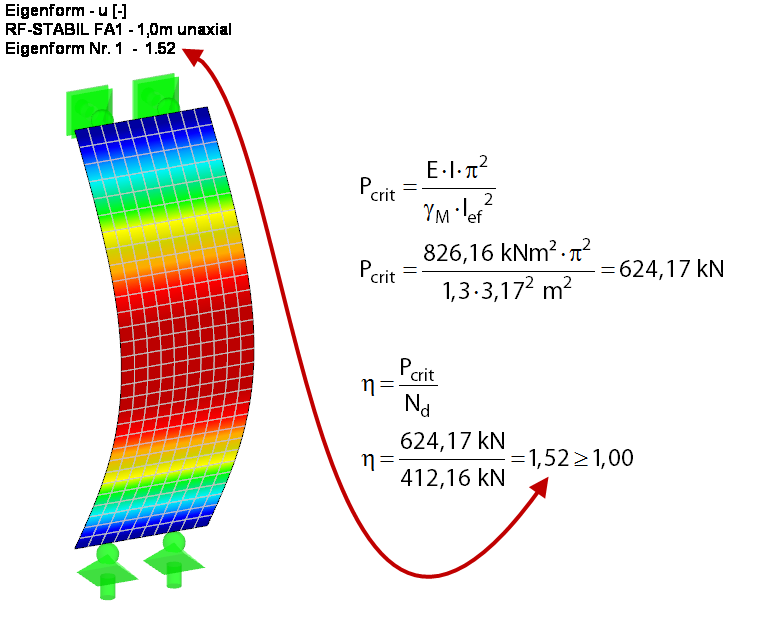
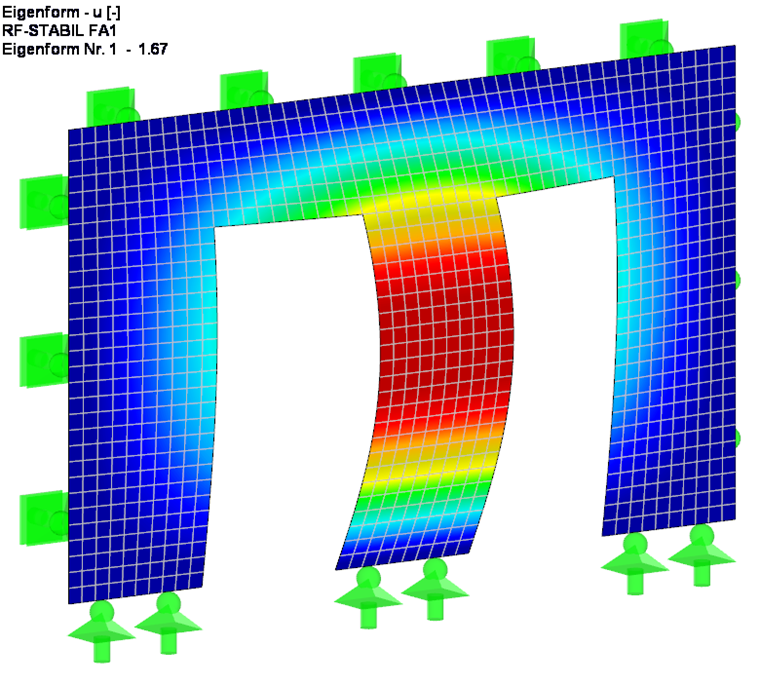
Для того, чтобы лучше оценить проблему потери устойчивости в данном случае, нужно сначала определить по методу линейного статического расчета критическую нагрузку потери устойчивости, а также коэффициент критической нагрузки для сечения стены у идеальной однопролетной балки (см. рисунок 4). Для этого коэффициент критической нагрузки определяется аналитически, а также с помощью дополнительного модуля RF-STABILITY. В случае расчета по МКЭ создается загружение без собственного веса, и затем непосредственно применяется результирующая нагрузка. Редукция жесткости, связанная с частичным коэффициентом надежности γM, активируется в параметрах расчета загружения. Результат обоих расчетов будет абсолютно одинаковым.
Как и ожидалось, с учетом дополнительной жесткости, возникающей из-за дверной перемычки, коэффициент критической нагрузки 1,67 равен 1,67.
Коэффициент критической нагрузки указывает число, на которое необходимо умножить нагрузку, чтобы модель под действием соответствующей нагрузки стала неустойчивой (потеря устойчивости). Следовательно: Коэффициент критической нагрузки менее 1,00 означает, что конструкция нестабильна. Только положительный коэффициент критической нагрузки, превышающий 1,00, означает, что нагрузка от заданных осевых сил, умноженная на этот коэффициент, приводит к разрушению конструкции при потере устойчивости. Однако необходимо выполнить расчет на устойчивость по норме 1995-1-1, так как коэффициент критической нагрузки или критическая нагрузка потери устойчивости на практике могут не быть правильными из-за влияния несовершенств (нет прямого стержня или поверхности), эксцентриситетов нагрузки и введение и работа материала, отличная от закона Гука, не учитываются. Подробности в расчетах затем подробнее объясняются в следующей статье данной серии.
.png?mw=512&hash=4e74affa9ad0c7b703151c5085ac9b8e59171c23)
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)