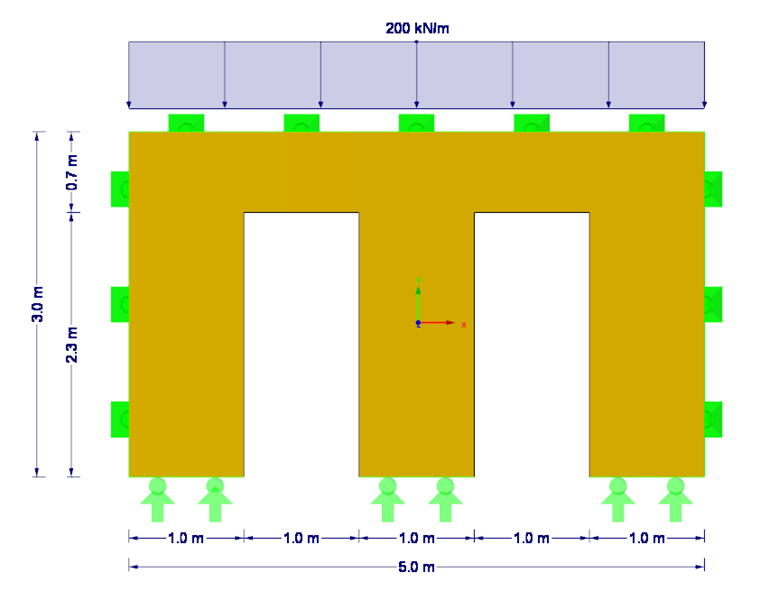
V našem příkladu posoudíme na prostý vzpěr stěnu z křížem lepeného dřeva s podepřením na čtyřech stranách a se dvěma dveřními otvory (viz obr. 01). Za rozhodující můžeme přitom považovat mezidveřní úsek ve stěně.
Posouzení na vzpěr v ohybu lze provést podle [1] metodou náhradního prutu podle kapitoly 6.3.2 s vnitřními silami podle lineární statické analýzy nebo podle kapitoly 5.4.4 se zohledněním imperfekcí. V obou případech je třeba se řídit kap. 2.2.2. Při výpočtu vnitřních sil podle teorie druhého řádu je přitom třeba vycházet z průměrných hodnot tuhostních vlastností (modul pružnosti a smykový modul) vydělených dílčím součinitelem γM podle 2.4.1(2)P. Kromě toho [2] NCI NA.9.3.3 definuje situace, kdy je třeba provést posouzení stability podle teorie druhého řádu pro rovinné konstrukční prvky. Jestliže je splněna podmínka NA.150, smí se posouzení stability provést jak metodou náhradního prutu tak podle teorie druhého řádu. Jinak je třeba konstrukční prvky posuzovat výlučně podle teorie druhého řádu.
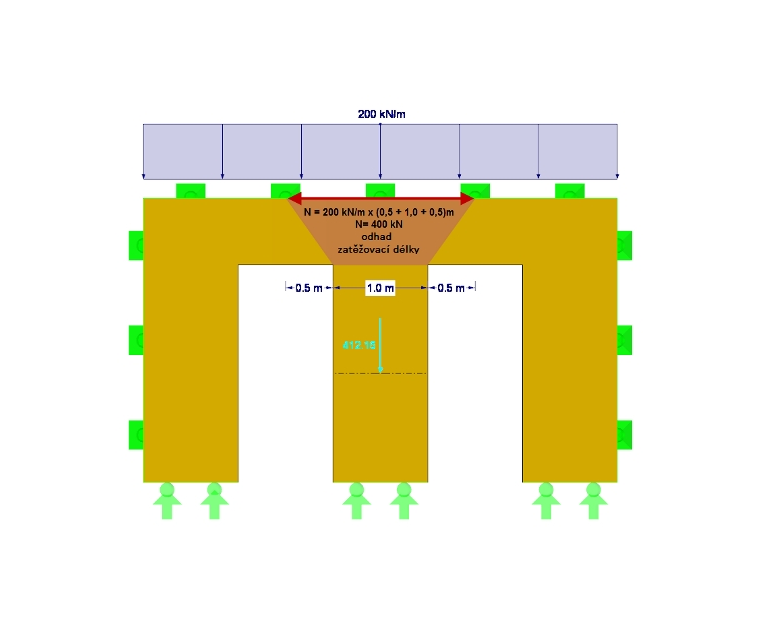
Nejdříve ověříme, zda je splněna podmínka NA.150. Potřebujeme přitom znát působící normálovou sílu Nd, ohybovou tuhost E∙I podél lokální osy y, dílčí součinitel γM pro křížem lepené dřevo a dále vzpěrnou délku posuzovaného mezidveřního úseku stěny. Zatěžovací délku stanovíme přibližně na 0,5 m + 1,0 m + 0,5 m = 2,0 m. Tlaková síla Nd pak činí 200 kN/m ∙ 2 m = 400 kN (bez uvážení vlastní tíhy). Máme také možnost určit přesnou hodnotu tlakové síly při zohlednění vlastní tíhy, a to na základě výslednice na řezu v programu RFEM (viz obr. 02). Při uvážení ortotropie a vlastní tíhy činí výsledná tlaková síla 412 kN.
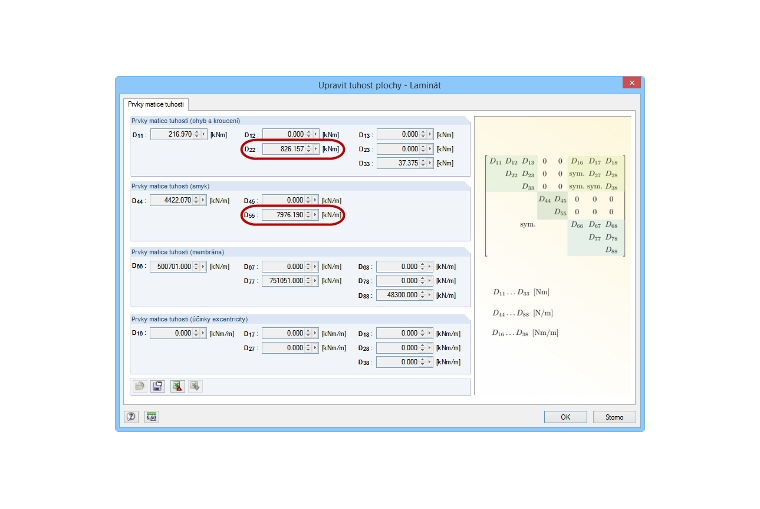
Ohybovou tuhost můžeme zjistit přímo z matice tuhosti dané plochy (viz obr. 03). Vybrali jsme přitom stěnu od společnosti Stora Enso typu CLT 100 C5s. Ohybová tuhost ve směru y činí 826,16 kNm ∙ 1,0 m = 826,16 kNm².
Za součinitel spolehlivosti se podle [2] dosadí hodnota 1,3. Při výpočtu vzpěrné délky se má pro křížem lepené dřevo zohlednit také smyková tuhost ve směru y (viz obr. 03). Protože se jedná o Eulerův případ 2, má součinitel vzpěrné délky β hodnotu 1,0.
Vymezovací kritérium není splněno s 2,55 > 1,00; proto je třeba provést posouzení stability podle teorie druhého řádu. Jelikož zde máme téměř prutový konstrukční prvek, posoudíme ho v následujících příspěvcích oběma metodami.
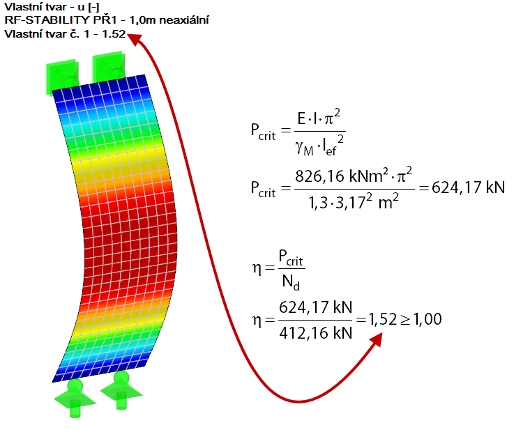
Pro lepší posouzení problému boulení se v tomto případě nejdříve stanoví kritické zatížení a součinitel kritického zatížení pro stěnový úsek na ideálním nosníku o jednom poli pomocí lineární statické analýzy (viz obr. 4). Součinitel kritického zatížení se přitom stanoví analyticky a pak také v přídavném modulu RF-STABILITY. Pro řešení metodou konečných prvků vytvoříme zatěžovací stav bez vlastní tíhy a použijeme přímo zatížení z výslednice. Redukci tuhosti s ohledem na dílčí součinitel γM aktivujeme v parametrech výpočtu zatěžovacího stavu. Oba výpočty se ve výsledku přesně shodují.
Pokud zohledníme přídavnou tuhost od nadedveřního překladu, součinitel kritického zatížení se podle očekávání pro celou konstrukci mírně zvýší na 1,67.
Součinitel kritického zatížení udává, jakým součinitelem je třeba vynásobit zatížení, aby při něm konstrukce ztratila stabilitu (vybočila). To znamená, že: pokud je součinitel kritického zatížení menší než 1,00, konstrukce je nestabilní. Pouze kladná hodnota součinitele kritického zatížení větší než 1,00 vypovídá o tom, že při zatížení vlivem působících normálových sil, které vynásobíme daným součinitelem, dochází k stabilitnímu selhání konstrukce ve vzpěru. Je ovšem třeba dodatečně provést stabilitní analýzu podle EN 1995-1-1, protože součinitel kritického zatížení, respektive kritické zatížení při vzpěru nejsou v praxi na straně bezpečnosti, protože se neuvažují účinky imperfekcí (žádný prut ani plocha nejsou rovné), excentrické působení zatížení ani chování materiálu odchylné od Hookova zákona. Posouzení provedeme v našem dalším příspěvku.
.png?mw=512&hash=4e74affa9ad0c7b703151c5085ac9b8e59171c23)
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)