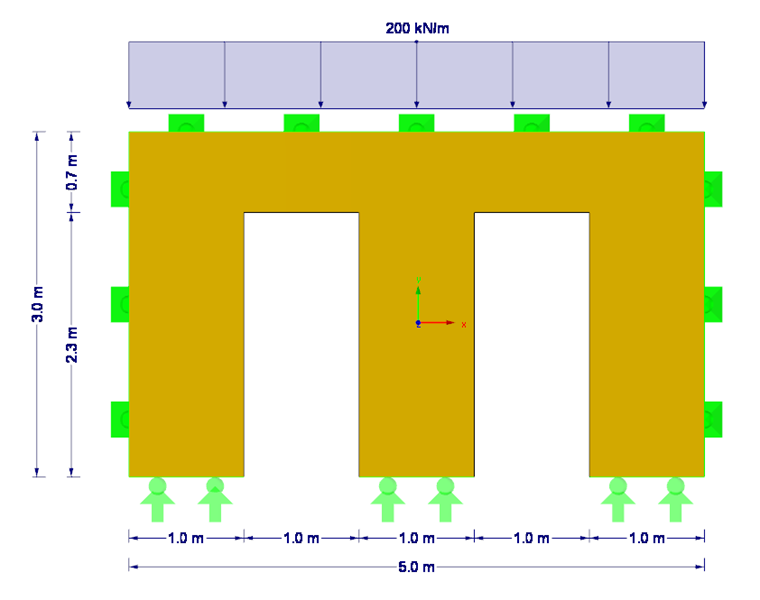
本示例介绍的是四边形正交胶合木墙的弯曲屈曲分析,该墙面有两个洞口(见图 1)。 在这种情况下,主导工况是门之间的墙体截面。
根据[1]使用等效杆件法进行弯曲屈曲分析,第 6.3.2 章有内力,考虑缺陷后可按照第 5.4.4 章一阶分析。 这两种情况下都必须遵守章节 2.2.2。 上面的刚度参数(弹性模量和剪切模量)的平均值除以分项系数 γM ,得出按照2.4.1(2)P的二阶分析方法[SCHOOL.INSTITUTION] 此外,在[2] NCI NA.9.3.3 中定义了对平面结构构件必须根据二阶分析进行稳定性分析的情况。 如果满足公式 NA.150,则稳定性分析可以使用等效杆件设计以及二阶分析进行计算。 否则,只能根据二阶理论进行设计。
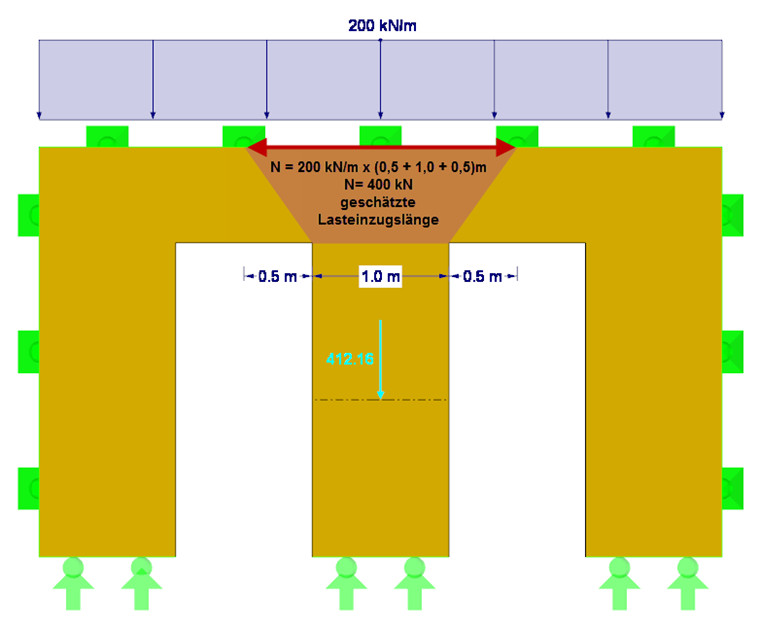
首先检查,是否满足公式 NA.150。 这需要轴力 Nd ,沿局部轴 y 轴的抗弯刚度 E∙I,分项系数(对于正交胶合木)为 γM ,以及门之间相应墙体截面的有效长度。 施加荷载的长度大约为 0.5 m + 1.0 m + 0.5 m = 2.0 m。 由此得出的压力 Nd是 200 kN/m ∙ 2 m = 400 kN(不考虑自重)。 此外,也可以通过使用 RFEM 中的截面合力得到考虑自重的精确计算压力(见图 2)。 在受到正交各向异性和自重影响后,得出的压力为 412 kN。
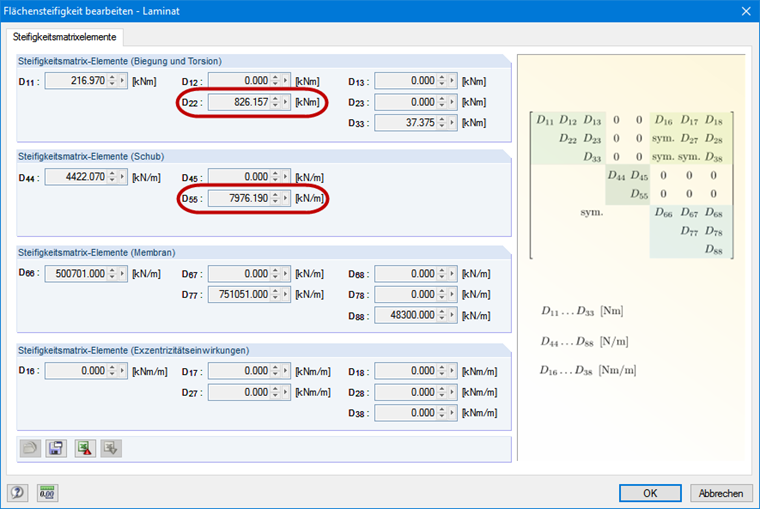
抗弯刚度可以直接从面的刚度矩阵中导出(见图 3)。 在这里选择 Stora Enso 生产的 CLT 墙面,类型 CLT 100 C5s。 沿 y 方向的抗弯刚度为 826,16 kNm ∙ 1,0 m = 826,16 kNm²。
根据 [2] 的方法应用分项系数 1.3。 对于正交胶合木,在确定有效长度时还要考虑在 y 方向上的抗剪刚度(见图 3)。 有效长度系数 β 1.0,按照欧拉工况 2。
不满足划界准则,2.55 > 1.00;因此必须按照二阶分析方法进行稳定性分析。 因为分析的是近似线性杆件,所以在以后的文章中将分别介绍这两种方法。
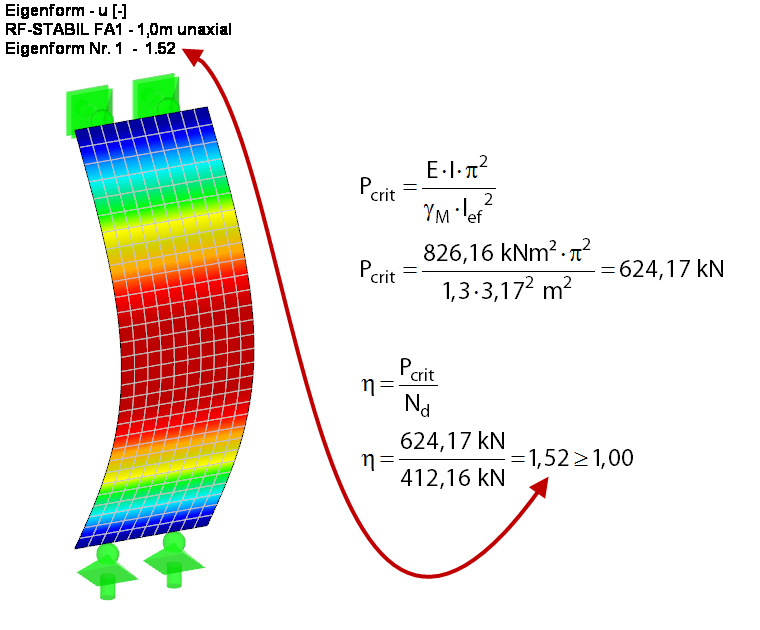
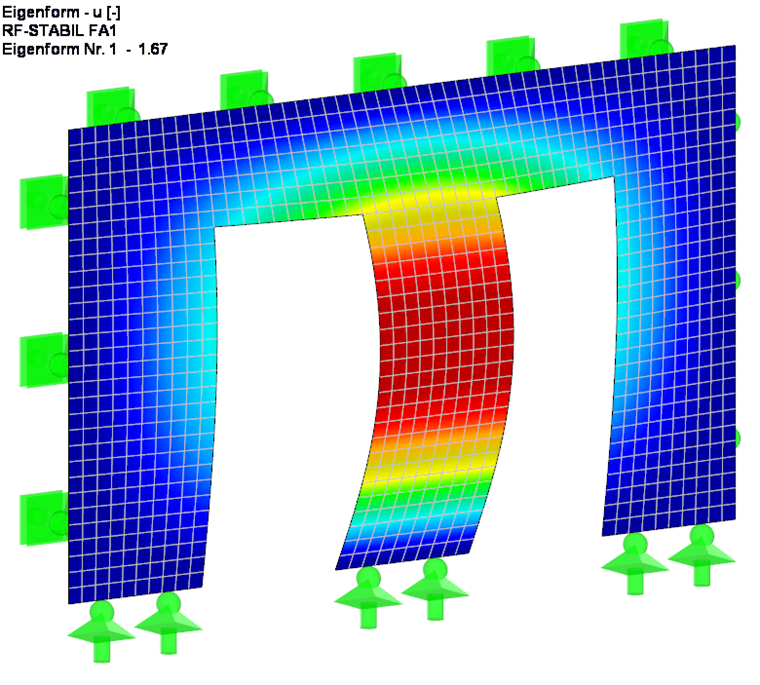
为了更好地估计屈曲问题,首先根据一阶静力分析确定理想单跨梁的临界屈曲荷载和临界荷载系数(见图 4)。 为此,临界荷载系数可以通过分析和使用附加模块 RF-STABILITY 来确定。 对于有限元方法,首先创建一个没有自重的荷载工况,然后直接施加结果荷载。 与分项系数 γM相关的刚度折减在荷载工况的计算参数中激活。 两次计算的结果完全相同。
考虑到门过梁产生的附加刚度,整个结构的临界荷载系数与预期的一样,为略大的 1.67。
临界荷载系数表示模型在荷载乘以多大倍数后才会变得不稳定(屈曲)。 因此: 如果荷载系数小于1,说明结构在当前荷载下已经失稳。 临界荷载系数必须大于1,才能保证结构的稳定。 然而,必须按照 1995-1-1 进行稳定性分析,因为临界荷载系数或临界屈曲荷载在实践中可能并不正确,引言,以及不同于胡克定律的材料行为不考虑。 在下一篇文章中将详细介绍这些设计。