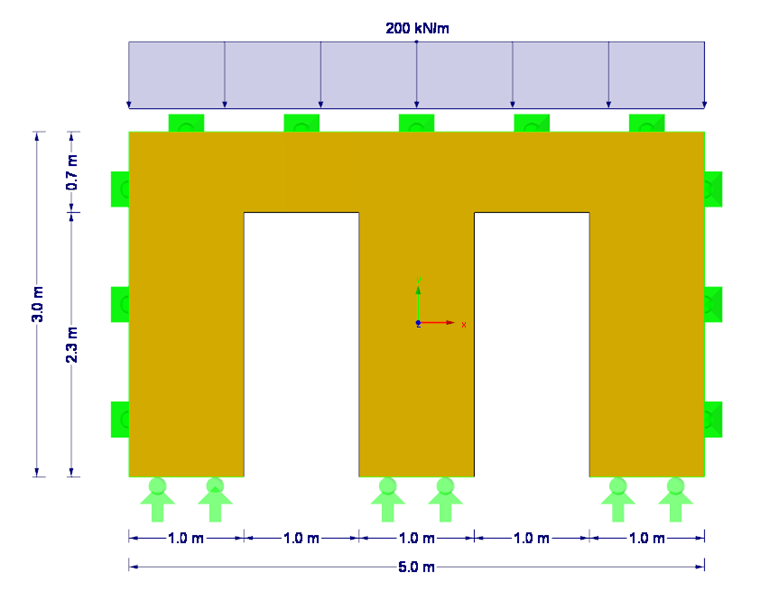
Ten przykład przedstawia analizę wyboczenia giętnego czworobocznej ściany z drewna klejonego krzyżowo z dwoma otworami drzwiowymi (patrz Rysunek 1). Decydującym przypadkiem jest przekrój ściany pomiędzy drzwiami.
Analiza wyboczenia giętnego może być przeprowadzona zgodnie z [1] przy użyciu metody pręta zastępczego zgodnie z rozdz. 6.3.2 z siłami wewnętrznymi zgodnie z liniową analizą statyczną lub zgodnie z rozdz. 5.4.4 z uwzględnieniem imperfekcji. W obu przypadkach należy przestrzegać sekcji 2.2.2. W tym celu należy użyć średnich wartości parametrów sztywnościowych (modułu sprężystości i modułu sprężystości przy ścinaniu) podzielonych przez współczynnik częściowy γM do określenia sił wewnętrznych zgodnie z analizą drugiego rzędu zgodnie z 2.4.1(2)P. Ponadto w [2] NCI NA.9.3.3 zdefiniowano sytuacje, w których dla płaskich elementów konstrukcyjnych należy przeprowadzić analizę stateczności według teorii drugiego rzędu. Jeżeli spełnione jest równanie NA.150, analiza stateczności może być przeprowadzana przy użyciu wymiarowania pręta zastępczego lub analizy drugiego rzędu. W przeciwnym razie obliczenia muszą być przeprowadzane wyłącznie zgodnie z analizą drugiego rzędu.
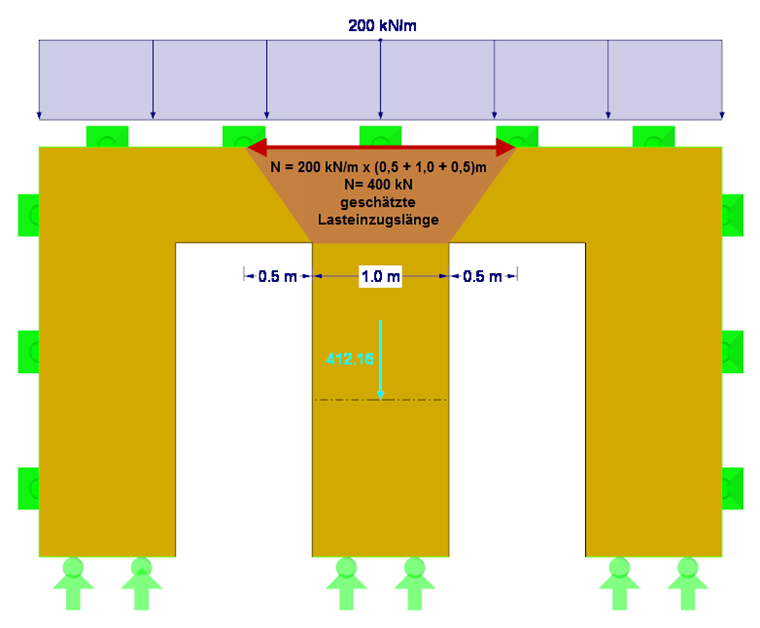
Najpierw należy sprawdzić, czy spełnione jest równanie NA.150. Wymaga to zastosowania działającej siły osiowej Nd, sztywności na zginanie E∙I wzdłuż lokalnej osi y , współczynnika częściowego γM dla drewna klejonego krzyżowo oraz długości efektywnej odpowiedniego odcinka ściany między drzwiami. Długość przyłożenia obciążenia wynosi w przybliżeniu 0,5 m + 1,0 m + 0,5 m = 2,0 m. Zatem wynikowa siła ściskająca Nd wynosi 200 kN/m ∙ 2 m = 400 kN (bez uwzględnienia ciężaru własnego). Alternatywnie, dokładne określenie siły ściskającej z uwzględnieniem ciężaru własnego można uzyskać, wykorzystując siły wypadkowe przekroju w programie RFEM (patrz Rysunek 2). W wyniku ortotropii i ciężaru własnego wynikowa siła ściskająca wynosi 412 kN.
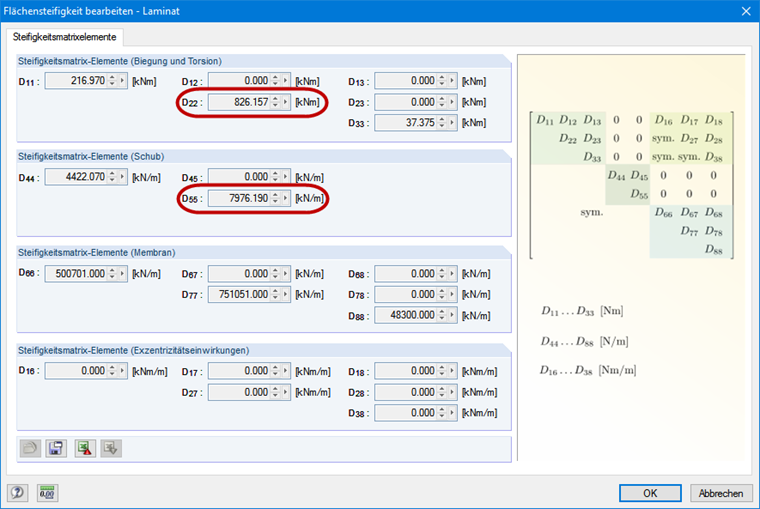
Sztywność na zginanie można odjąć bezpośrednio od macierzy sztywności powierzchni (patrz Rysunek 3). Tutaj wybierana jest powierzchnia ściany firmy Stora Enso typu CLT 100 C5s. Wynikowa sztywność na zginanie w kierunku y wynosi 826,16 kNm ∙ 1,0 m = 826,16 kNm².
Współczynnik częściowy 1,3 został zastosowany zgodnie z [2]. Aby określić długości efektywne, należy uwzględnić również sztywność na ścinanie w kierunku y dla drewna klejonego krzyżowo (patrz Rysunek 3). Współczynnik długości efektywnej β wynoszący 1,0 jest stosowany zgodnie z przypadkiem Eulera 2.
Kryterium delimitacji nie jest spełnione, jeżeli 2,55 > 1,00; dlatego konieczne jest przeprowadzenie analizy stateczności według analizy drugiego rzędu. Ponieważ analizowany jest pręt prawie liniowy, obie metody zostaną wyjaśnione w kolejnych artykułach.
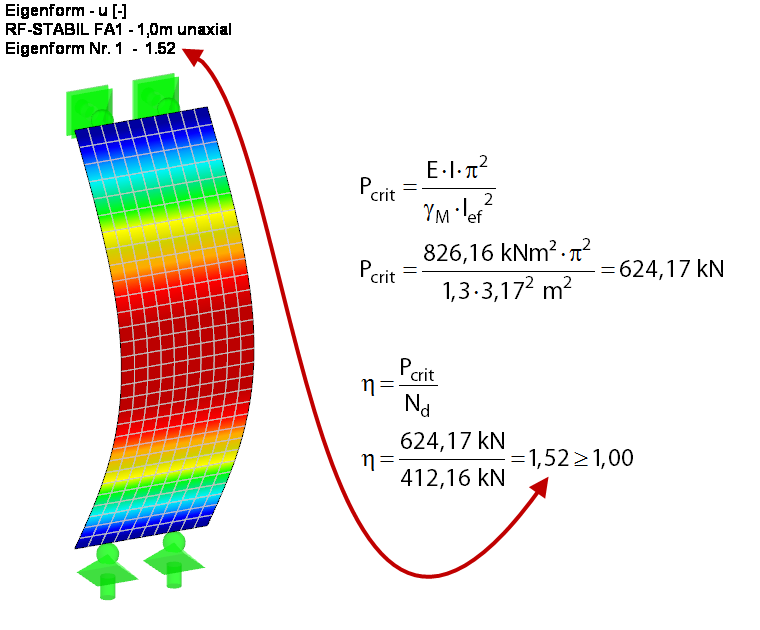
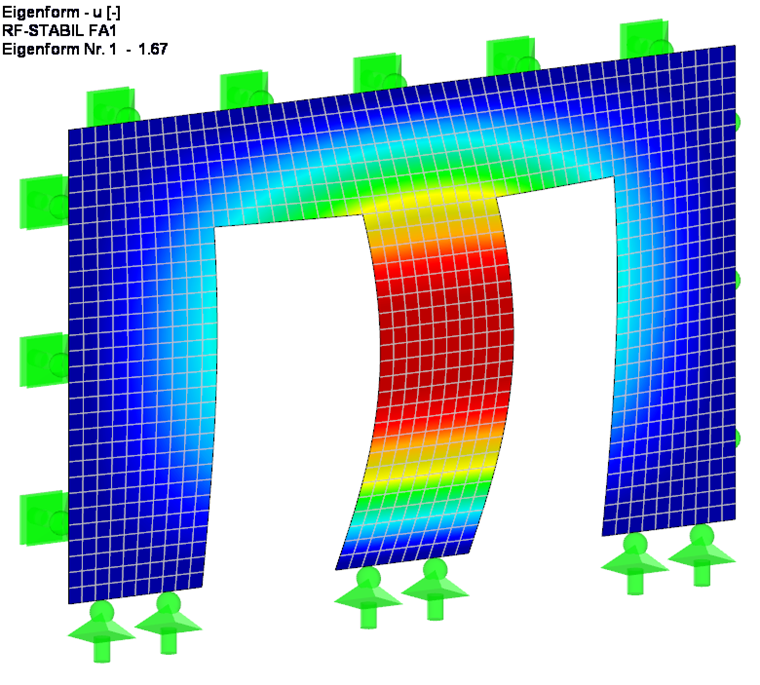
Aby lepiej oszacować problem wyboczenia w tym przypadku, najpierw określane jest obciążenie krytyczne oraz współczynnik obciążenia krytycznego dla przekroju ściany w miejscu idealnej belki jednoprzęsłowej, zgodnie z liniową analizą statyczną (patrz Rysunek 4). W tym celu współczynnik obciążenia krytycznego jest określany analitycznie oraz przy użyciu modułu dodatkowego RF-STABILITY. W przypadku rozwiązania MES tworzony jest przypadek obciążenia bez ciężaru własnego, a wynikowe obciążenie jest przykładane bezpośrednio. Redukcja sztywności odniesiona do częściowego współczynnika bezpieczeństwa γM jest aktywowana w parametrach obliczeniowych przypadku obciążenia. Wynik obu obliczeń jest dokładnie taki sam.
Biorąc pod uwagę dodatkową sztywność wynikającą z nadproża bramy, zgodnie z oczekiwaniami, współczynnik obciążenia krytycznego wynosi nieco większy, 1,67.
Współczynnik obciążenia krytycznego wskazuje liczbę, przez którą należy pomnożyć obciążenie, aby model pod powiązanym obciążeniem stał się niestateczny (wyboczenie). Z tego wynika: Współczynnik obciążenia krytycznego mniejszy niż 1,00 oznacza, że konstrukcja jest niestateczna. Tylko dodatni współczynnik obciążenia krytycznego większy niż 1,00 oznacza, że obciążenie wywołane wstępnie zdefiniowanymi siłami osiowymi pomnożone przez ten współczynnik powoduje utratę stateczności konstrukcji. Jednak zgodnie z 1995-1-1 należy przeprowadzić analizę stateczności, ponieważ w praktyce współczynnik obciążenia krytycznego lub krytycznego obciążenia wyboczeniowego może nie być prawidłowy, jak imperfekcje (żaden pręt lub powierzchnia nie jest prosta), mimośrody obciążenia i zachowanie materiału odbiegające od prawa Hooke'a. Obliczenia zostały opisane w kolejnym artykule z tej serii.
.png?mw=512&hash=4e74affa9ad0c7b703151c5085ac9b8e59171c23)
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)