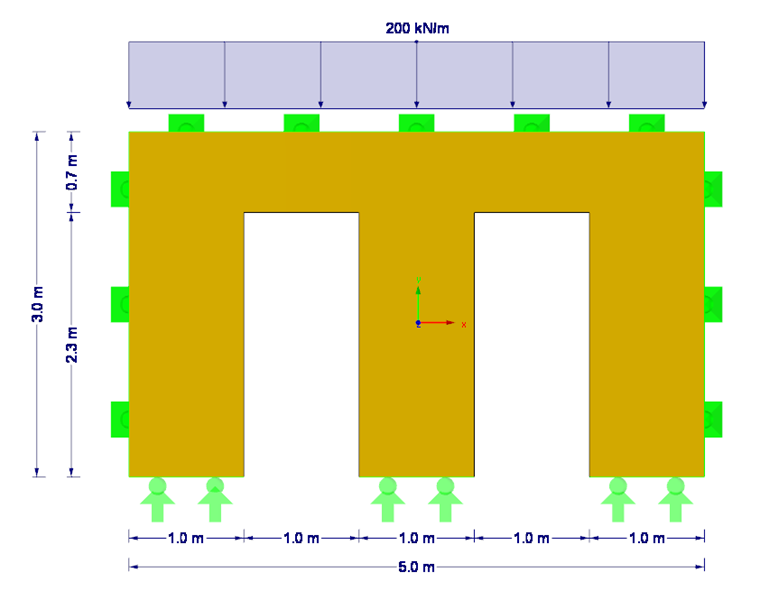
Cet exemple présente l’analyse du flambement par flexion d’un mur quadrilatéral en bois lamellé-croisé avec deux ouvertures de porte (voir la Figure 01). Dans ce cas, le cas déterminant est la section de mur entre les portes.
L’analyse du flambement par flexion peut être effectuée selon [1] à l’aide de la méthode de barre équivalente selon le Chapitre 6.3.2 avec les efforts internes selon l’analyse statique linéaire, ou selon le Chapitre 5.4.4, en considérant les imperfections. Dans les deux cas, la Section 2.2.2 doit être respectée. Pour ce faire, les valeurs moyennes des paramètres de rigidité (module d'élasticité et module de cisaillement) divisées par le facteur partiel γM doivent être utilisées pour déterminer les efforts internes selon l'analyse du second ordre conformément à 2.4.1(2)P. De plus, [2] NCI NA.9.3.3 définit les situations dans lesquelles une analyse de stabilité doit être effectuée selon l'analyse du second ordre pour les composants structuraux 2D. Si l'équation NA.150 est remplie, les analyses de stabilité peuvent être calculées à l'aide du calcul de barre équivalente ainsi que de l'analyse du second ordre. Sinon, les vérifications doivent être effectuées exclusivement selon l'analyse du second ordre.
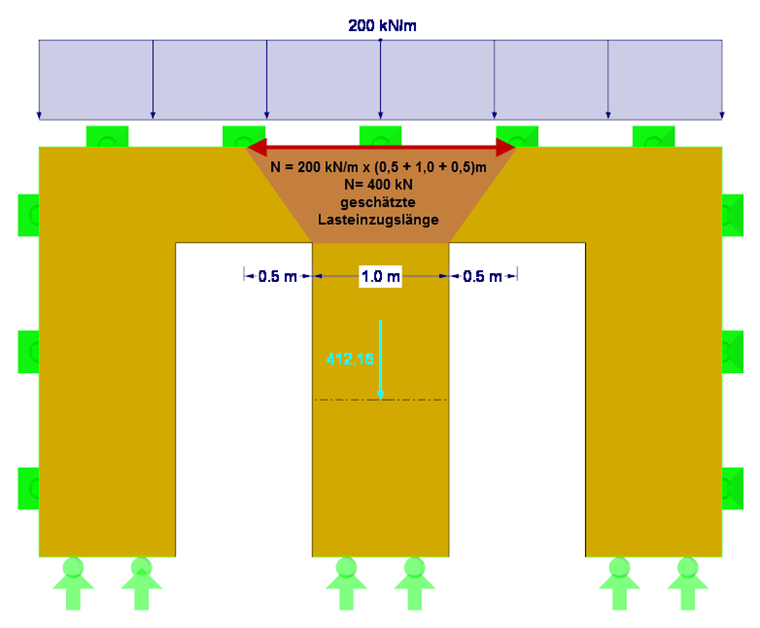
Il faut d'abord vérifier si l'équation NA.150 a été remplie. Cela nécessite l'effort normal agissant Nd, la rigidité en flexion E∙I le long de l'axe y local, le facteur partiel γM pour le bois lamellé-croisé et la longueur efficace de la section de paroi correspondante entre les portes. La longueur d'application de charge est définie approximativement à 0,5 m + 1,0 m + 0,5 m = 2,0 m. Ainsi, la force de compression résultante Nd est égale à 200 kN/m ∙ 2 m = 400 kN (sans considération du poids propre). Les efforts de compression peuvent également être déterminés avec précision en considérant le poids propre à l'aide des efforts résultants des sections dans RFEM (voir la Figure 02). En raison de l'orthotropie et du poids propre, la force de compression résultante est de 412 kN.
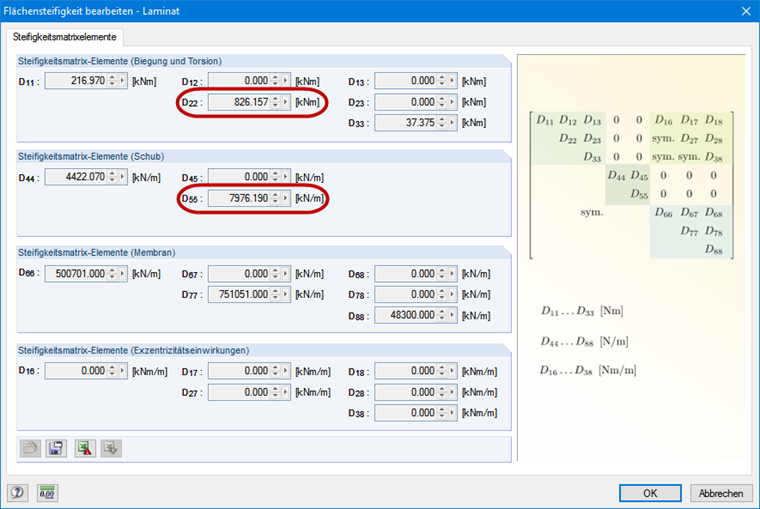
La rigidité en flexion peut être déduite directement à partir de la matrice de rigidité de la surface (voir la Figure 03). La surface du voile Stora Enso de type CLT CLT 100 C5s a été sélectionnée. La rigidité en flexion résultante dans la direction y est de 826,16 kNm ∙ 1,0 m = 826,16 kNm².
Le facteur partiel de 1,3 est appliqué selon [2]. Afin de déterminer ces longueurs, la rigidité en cisaillement dans la direction y doit également être considérée pour le bois lamellé-croisé (voir la Figure 03). Le facteur de longueur efficace β de 1,0 est utilisé selon le cas Euler 2.
le critère de délimitation n'est pas rempli 2,55 > 1,00 ; l'analyse de stabilité selon l'analyse du second ordre doit donc être effectuée. Étant donné qu'une barre presque linéaire est analysée, ces deux méthodes seront expliquées dans les prochains articles.
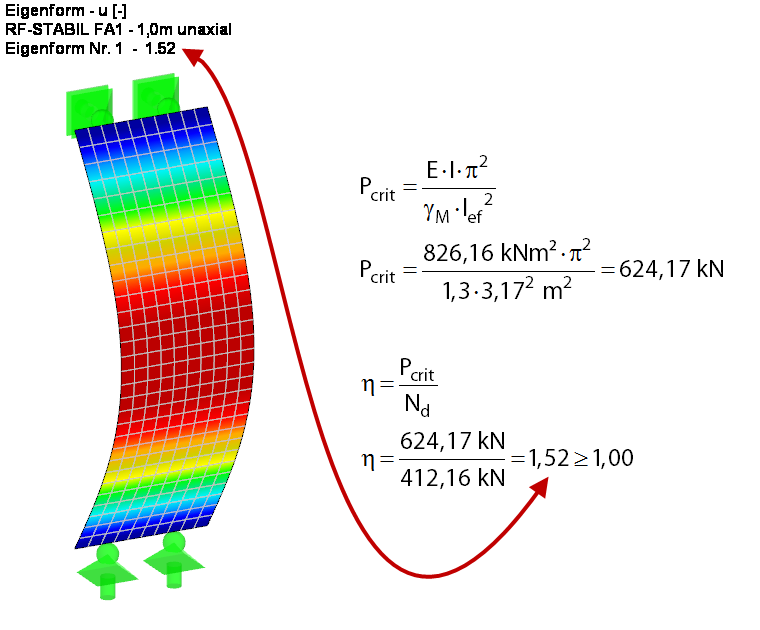
Afin de mieux estimer le problème de flambement dans ce cas, la charge critique de flambement ainsi que le facteur de charge critique pour la section de paroi au niveau de la poutre à travée idéale sont d'abord déterminés selon une analyse au premier ordre (voir la Figure 04). Pour ce faire, le facteur de charge critique est déterminé analytiquement et à l'aide du module additionnel RF-STABILITY. Pour la solution aux éléments finis, un cas de charge sans poids propre est créé et la charge résultante est appliquée directement. La réduction de rigidité liée au facteur de sécurité partielγM est activée dans les paramètres de calcul du cas de charge. Le résultat des deux calculs est identique.
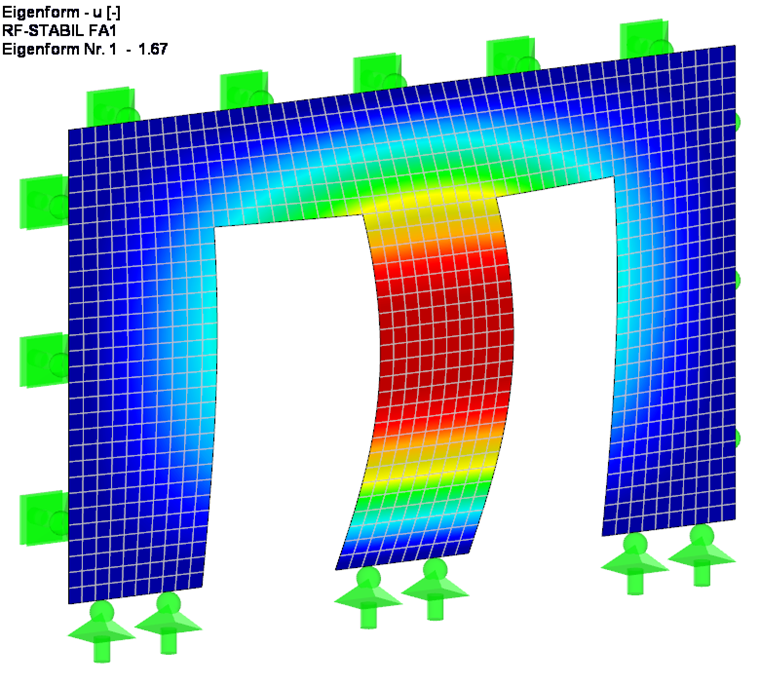
En considérant la rigidité supplémentaire résultant du linteau de porte, le facteur de charge critique légèrement plus élevé de 1,67 est obtenu sur l’ensemble de la structure, comme prévu.
Ce facteur de charge critique indique le nombre par lequel la charge doit être multipliée afin que le modèle soumis à la charge correspondante devienne instable (flambement). Par conséquent : Un facteur de charge critique inférieur à 1,00 signifie que la structure est instable. Seul un facteur de charge critique positif supérieur à 1,00 signifie que la charge due aux efforts normaux prédéfinis multipliés par ce facteur entraîne la rupture par flambement de la structure stable. Une analyse de stabilité doit cependant être effectuée selon la norme 1995-1-1 car le facteur de charge critique ou la charge critique de flambement peut ne pas être correct dans la pratique, en raison des effets des imperfections (aucune barre ou surface n'est droite), des excentrements de charge ainsi que le comportement du matériau qui diffère de la loi de Hooke ne sont pas considérés. Ces vérifications sont expliquées dans l'article suivant de cette série.