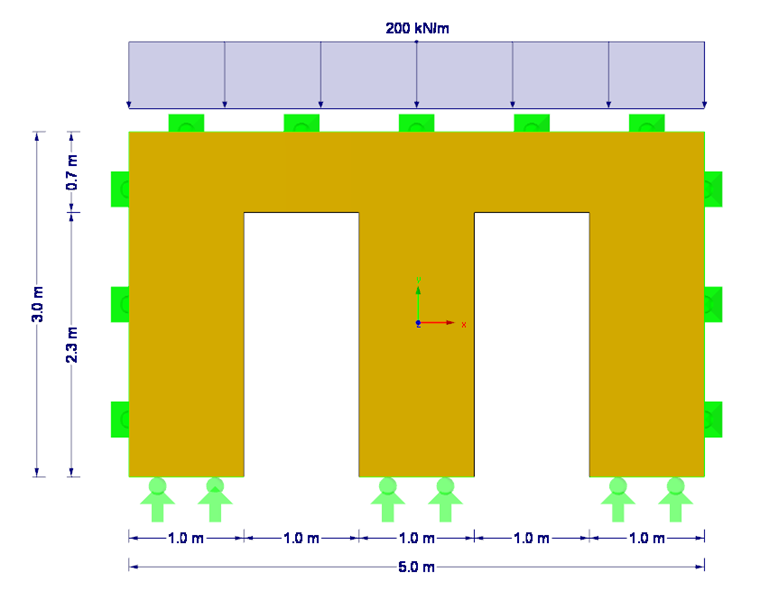
Questo esempio presenta un'analisi di instabilità flessionale di una parete quadrangolare in legno lamellare a strati incrociati con due aperture delle porte (vedere la Figura 1). In questo caso, il caso determinante è la sezione della parete tra le porte.
L'analisi di instabilità flessionale può essere eseguita secondo [1] con il metodo dell'asta equivalente secondo il Capitolo 6.3.2 con forze interne secondo l'analisi statica lineare, o secondo il Capitolo 5.4.4, considerando le imperfezioni. In entrambi i casi, la Sezione 2.2.2 deve essere rispettata. Per questo, i valori medi dei parametri di rigidezza (modulo di elasticità e modulo di taglio) divisi per il coefficiente parziale γM dovrebbero essere utilizzati per determinare le forze interne secondo l'analisi del secondo ordine in conformità con 2.4.1(2)P. Inoltre, [2] NCI NA.9.3.3 definisce quelle situazioni in cui un'analisi di stabilità deve essere eseguita secondo l'analisi del secondo ordine per componenti strutturali planari. Se l'equazione NA.150 è soddisfatta, le analisi di stabilità possono essere calcolate utilizzando la verifica dell'asta equivalente e l'analisi del secondo ordine. In caso contrario, i progetti devono essere eseguiti esclusivamente secondo l'analisi del secondo ordine.
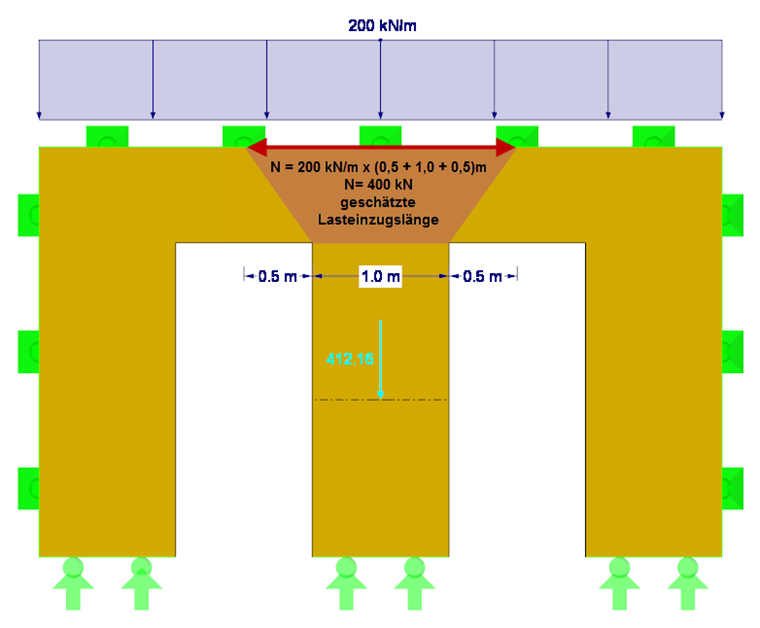
Innanzitutto, è necessario verificare se l'equazione NA.150 è stata soddisfatta. Ciò richiede la forza assiale agente Nd, la rigidezza flessionale E∙I lungo l'asse locale y, il coefficiente parziale γM per il legno lamellare a strati incrociati e la lunghezza efficace della rispettiva sezione di parete tra le porte. La lunghezza di applicazione del carico è impostata a circa 0,5 m + 1,0 m + 0,5 m = 2,0 m. Pertanto, la forza di compressione risultante Nd è 200 kN/m ∙ 2 m = 400 kN (senza considerare il peso proprio). In alternativa, la determinazione esatta della forza di compressione considerando il peso proprio può essere ottenuta utilizzando le forze risultanti della sezione in RFEM (vedere la Figura 2). A causa dell'ortotropia e del peso proprio, la forza di compressione risultante è 412 kN.
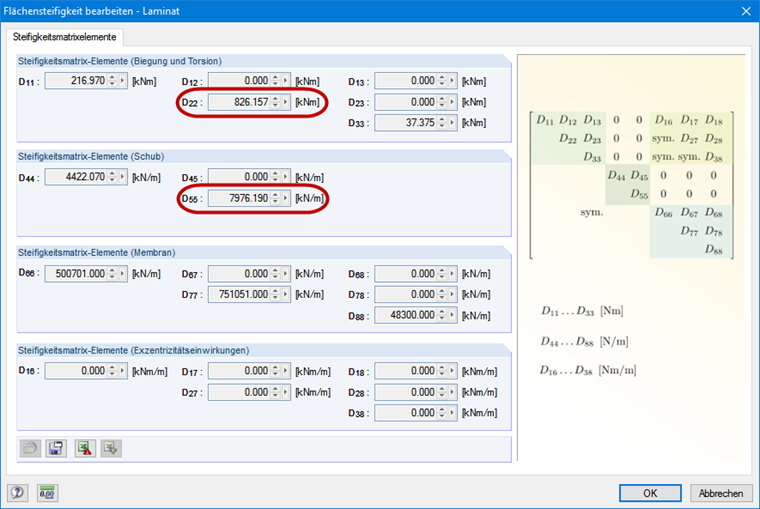
La rigidezza flessionale può essere dedotta direttamente dalla matrice di rigidezza della superficie (vedere la Figura 3). Qui, viene selezionata la superficie della parete di Stora Enso del tipo CLT CLT 100 C5s. La rigidezza flessionale risultante nella direzione y è 826,16 kNm ∙ 1,0 m = 826,16 kNm².
Il coefficiente parziale di 1.3 è applicato secondo [2]. Per determinare le lunghezze efficaci, la rigidezza a taglio nella direzione y dovrebbe essere considerata anche per il legno a strati incrociati (vedere la Figura 3). Il coefficiente di lunghezza efficace β di 1.0 è utilizzato secondo il caso di Eulero 2.
Il criterio di delimitazione non è soddisfatto con 2.55 > 1.00; pertanto, è necessario eseguire l'analisi di stabilità secondo l'analisi del secondo ordine. Poiché viene analizzata un'asta quasi lineare, entrambi i metodi saranno spiegati nei miei prossimi articoli.
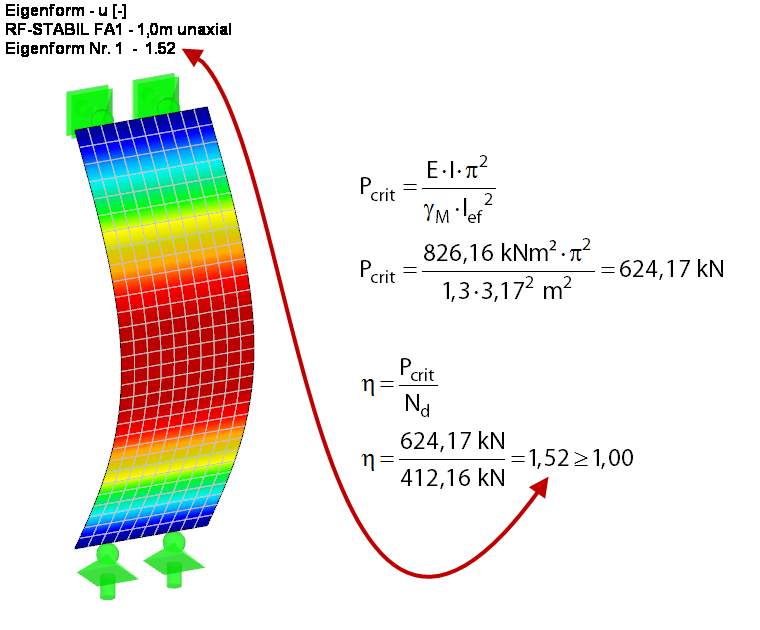
Al fine di stimare meglio il problema di instabilità in questo caso, il carico critico e il coefficiente di carico critico per la sezione di parete sulla trave ideale a una campata vengono prima determinati secondo l'analisi statica lineare (vedere la Figura 4). Per questo, il coefficiente di carico critico è determinato analiticamente e utilizzando il modulo aggiuntivo RF-STABILITY. Per la soluzione FEM, viene creato un caso di carico senza peso proprio e il carico risultante viene applicato direttamente. La riduzione di rigidezza relativa al coefficiente di sicurezza parziale γM è attivata nei parametri di calcolo del caso di carico. Il risultato di entrambi i calcoli è esattamente lo stesso.
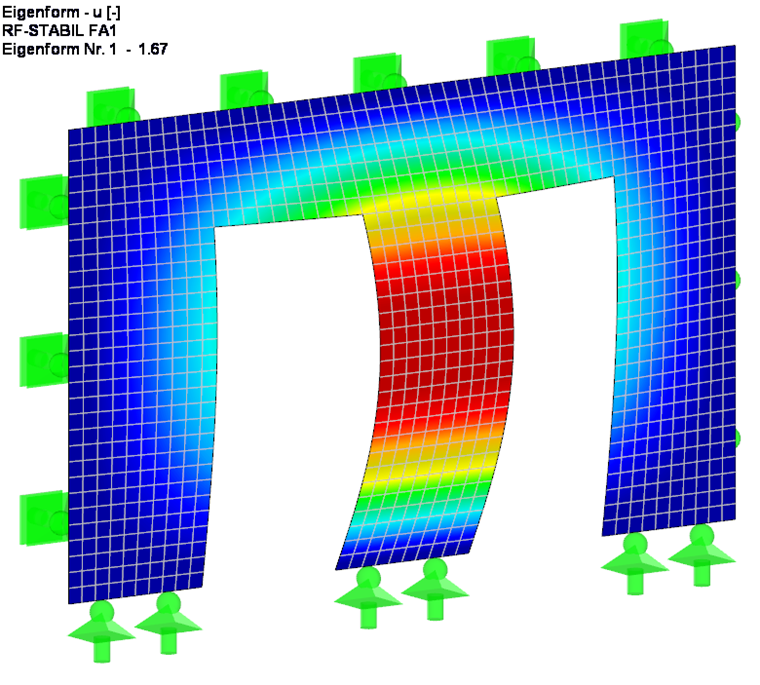
Tenendo conto della rigidezza aggiuntiva risultante dall'architrave della porta, il coefficiente di carico critico leggermente più grande di 1,67 risulta sull'intera struttura, come previsto.
Questo coefficiente di carico critico indica il numero per il quale il carico deve essere moltiplicato in modo che il modello sotto il carico associato diventi instabile (instabilità). Ne segue: Un coefficiente di carico critico inferiore a 1,00 indica che la struttura è instabile. Solo un coefficiente di carico critico positivo maggiore di 1,00 indica che il carico dovuto alle forze assiali predefinite moltiplicato per questo coefficiente porta alla rottura per instabilità della struttura stabile. Tuttavia, un'analisi di stabilità deve essere eseguita secondo 1995-1-1 perché il coefficiente di carico critico o il carico critico di instabilità potrebbero non essere corretti nella pratica, poiché gli effetti delle imperfezioni (nessuna asta o superficie è diritta), eccentricità del carico introduzione e il comportamento del materiale divergente dalla legge di Hooke non sono considerati. I progetti sono spiegati nel prossimo articolo di questa serie.
.png?mw=512&hash=4e74affa9ad0c7b703151c5085ac9b8e59171c23)
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)