2937x

001527

Dipl.-Ing. (FH) Ulrich Lex

2018-07-11

Влияние линейной нагрузки на стеклопакет

Увеличивается доля стекла, используемого при планировке здания. Открытые, залитые светом здания = это типичный знак современной архитектуры. Однако при проектировании специализированным инженерам приходится сталкиваться с новыми проблемами. Одним из таких примеров являются стеклянные фасады высотой до потолка, нагруженные перилами. Влияние этой нагрузки, а также расчет деформации показаны в данной статье.

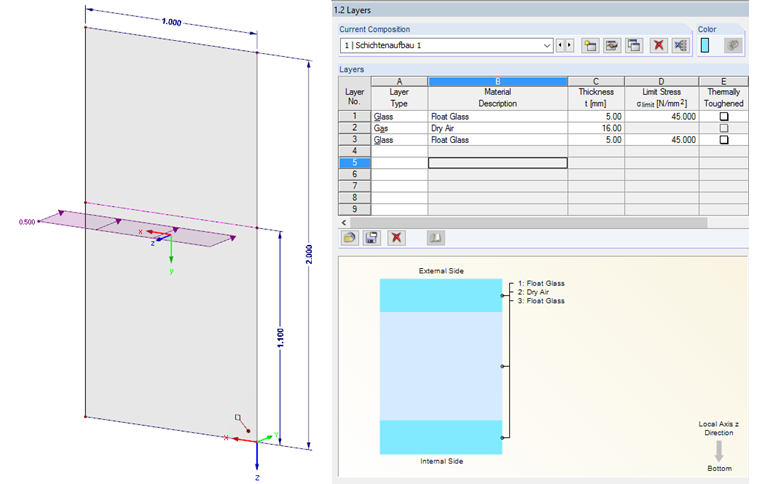
Расчетная модель

Изолированное остекление высотой 2 м и шириной 1 м служит в качестве расчетной модели. на которое на высоте 1, 10 м действует горизонтальная нагрузка размером 0, 5 кН. В качестве остекления выбрано стеклопакет 5-16-5.

Конструкция

Расчёт деформаций

Из-за замкнутого объема в промежуточном пространстве остекления расчет стеклянных пластин довольно сложен, Загрузка одной панели неизбежно вызывает также загрузку второй панели из-за связанной системы и, следовательно, распределения нагрузки на обе панели. Размер распределения нагрузки так будет всегда зависеть от выбранной конструкции остекления, точнее от жесткости отдельных пластин.

Программное обеспечение FEM (например, RFEM или RF-GLASS) обычно используется для анализа стеклопакетов, которое решает конструктивные проблемы. Тем не менее есть и формулы для аналитического обзора, которые приведены в литературе [1].

Потому были следующие значения деформаций были вычислены вручную.

Расчет объема при единичной нагрузке

u_{p, 1} = u_{p, 2} = b \cdot h \cdot \frac{a^{4}}{E \cdot d^{3}} \cdot B_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0501 = 0, 01145 \frac{м^{3}}{кН / м^{2}}

Формула 1

u_{q, 1} = b \cdot h \frac{a^{3}}{E \cdot d^{3}} \cdot C_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0365 = 0, 00834 \frac{м^{3}}{кН / м}

Формула 2

Расчет вспомогательных величин

α = α^{} = \frac{u_{p, 1} \cdot p_{a}}{V_{\Pr}} = \frac{0, 01145 \cdot 100}{1, 0 \cdot 2, 0 \cdot 0, 016} = 35, 78

Формула 3

Error converting from LaTeX to MathML

Формула 4

{ΔV}_{ex, 1} = u_{q, 1} \cdot q_{1} = 0, 00834 \cdot 0, 5 = 0, 00417 м^{2}

Формула 5

{Δp}_{ex} = \frac{{ΔV}_{ex, 1}}{V_{\Pr}} \cdot p_{a} = \frac{0, 00417}{1, 0 \cdot 2, 0 \cdot 0, 016} \cdot 100 = 13, 03 \frac{кН}{м^{2}}

Формула 6

Давление в пространстве между пластинами стеклопакета

Δp = φ \cdot ({Δp}_{ex} {Δp}_{c}) = 0, 0138 \cdot (13, 03 0) = 0, 180 \frac{кН}{м^{2}}

Формула 7

Теперь по этим значениям можно определить прогиб в середине пролета.

От распределенной нагрузки

f = \frac{q \cdot a^{3}}{E \cdot d^{3}} \cdot C_{f} = \frac{0.5 \cdot 1 . 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1045 = 0, 006 м

Формула 8

а также от внутренней нагрузки

f = \frac{Δp \cdot a^{4}}{E \cdot d^{3}} \cdot B_{f} = \frac{0.180 \cdot 1 . 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1151 = 0, 0022 м

Формула 9

наступает результирующая деформация нагруженного стекла
6,0 мм - 2,2 мм =3,8 мм.

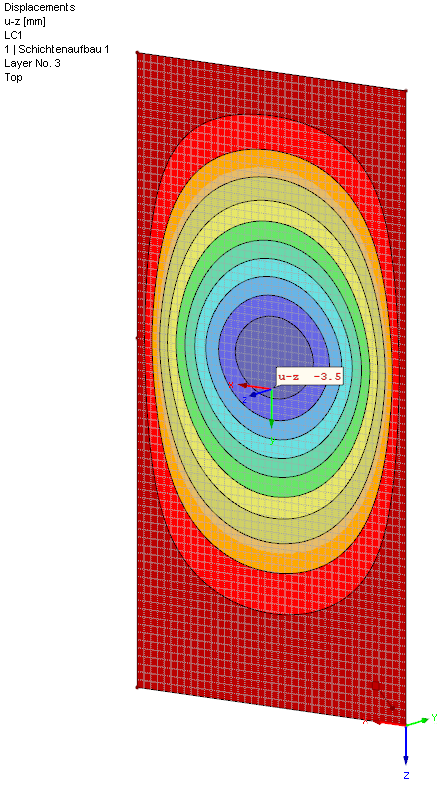
Это значение почти точно соответствует результату из модуля RF-GLASS: u_z = 3,5 мм. Видимые небольшие различия возникают потому, что формулы линеаризованы, а программа выполняет расчеты по теории больших деформаций и применяет подход, основанный на мембранной несущей способности.

Результаты деформации пластины 1

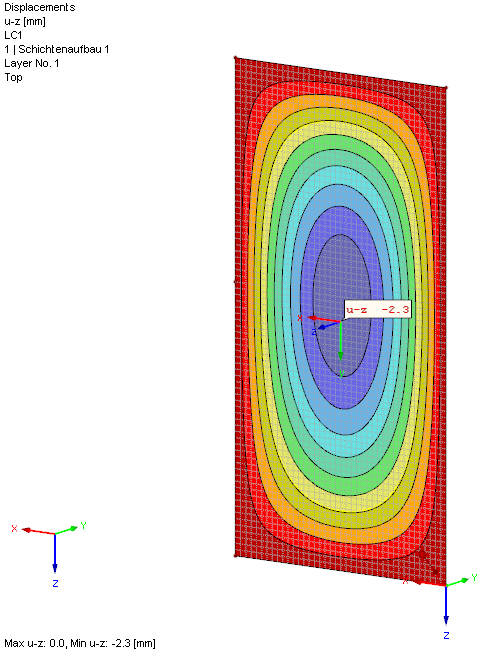
Вторично нагруженная пластина деформируется вследствие давления газа, преобладающего в промежуточном пространстве стеклопакета. Поскольку оба стекла имеют одинаковую жесткость, это значение уже было рассчитано с u_z = 2,2 мм.

Результаты деформации пластины 2

Заключение

Расчетная теория из [1] показывает, что даже связанные системы можно проверить вручную. Однако при изменении системы, например, при употреблении разной толщины пластин или применении многослойного безопасного стекла с одной стороны пластины, ручной расчет уже становится более сложным. Компьютерный расчет, например, с помощью RF-GLASS, предлагает инженерам-проектировщикам хорошую поддержку и помощь.

Автор

Г-н Лекс отвечает за разработку продуктов для стеклянных конструкций и за контроль качества программы RFEM. Помимо того, он оказывает также техническую поддержку нашим клиентам.

Ссылки

Программы для расчета и проектирования стеклянных конструкций

Ссылки

Feldmeier, F.: Klimabelastung und Lastverteilung bei Mehrscheiben-Isolierglas, Stahlbau 75, Seiten 467 - 478. Berlin: Ernst & Sohn, 2006

Скачивания

Файл модели в RFEM

2,47 MB

;