返回知识库

2975x

001527

Dipl.-Ing. （FH）Ulrich Lex

2018-07-11

线荷载在中空玻璃板上的影响

设计建筑物时使用玻璃的比例越来越多。开放的、光线充足的建筑物是现代的标志。这也为专业工程师在规划中带来了新挑战。跟框架一样高的玻璃幕墙通过一个扶手承载就是这样的一个例子。本文主要展示一下这种荷载的影响以及变形的计算。

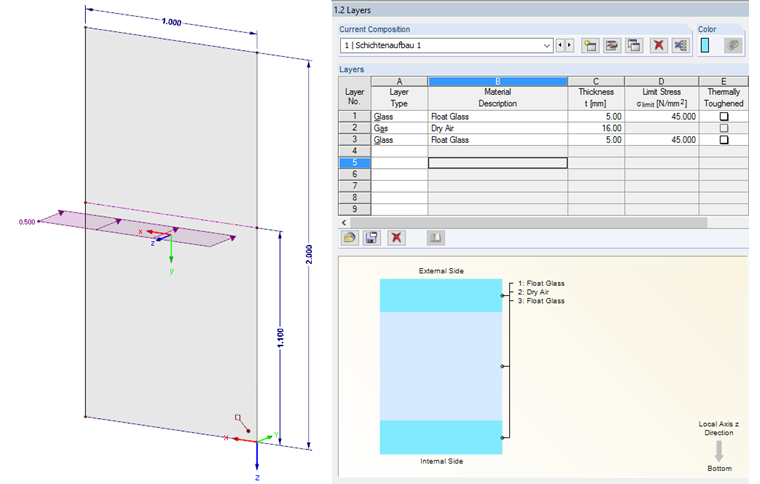
计算模型

计算模型中选择一块高 2 米、宽 1 米的中空玻璃板。施加水平荷载 0.5 kN 的荷载为 1.10 m。选择的玻璃为：中空玻璃 5-16-5。

结构

变形计算

玻璃板间的空间是封闭的，通过它计算两个板不是很复杂。荷载加载在一个板上，该系统是耦合的，也会同时对另一个板产生影响，因此荷载分布在两个板上。荷载分布的大小就与选择的玻璃板结构或者说单个玻璃板的刚度相关。

通常解决静力问题的有限元软件（例如：RFEM、RF-GLAS）用于计算中空玻璃。但是，解析视图的公式也显示在[1]中。

对于我们的示例，手动计算变形，将得出下面的值。

单位荷载作用下的体计算

ν_{p, 1} = ν_{p, 2} = b \cdot h \cdot \frac{a^{4}}{E \cdot d^{3}} \cdot B_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0501 = 0, 01145 \frac{m^{3}}{kN / m^{2}}

公式 1

ν_{q, 1} = b \cdot h \frac{a^{3}}{E \cdot d^{3}} \cdot C_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0365 = 0, 00834 \frac{m^{3}}{kN / m}

公式 2

计算辅助系数

α = α^{} = \frac{ν_{p, 1} \cdot p_{a}}{V_{\Pr}} = \frac{0, 01145 \cdot 100}{1, 0 \cdot 2, 0 \cdot 0, 016} = 35, 78

公式 3

Error converting from LaTeX to MathML

公式 4

{ΔV}_{ex, 1} = ν_{q, 1} \cdot q_{1} = 0, 00834 \cdot 0, 5 = 0, 00417 m^{2}

公式 5

{Δp}_{ex} = \frac{{ΔV}_{ex, 1}}{V_{\Pr}} \cdot p_{a} = \frac{0, 00417}{1, 0 \cdot 2, 0 \cdot 0, 016} \cdot 100 = 13, 03 \frac{kN}{m^{2}}

公式 6

板之间的压力

Δp = φ \cdot ({Δp}_{ex} {Δp}_{c}) = 0, 0138 \cdot (13, 03 0) = 0, 180 \frac{kN}{m^{2}}

公式 7

由该值可以计算在跨中的挠度。

由均布荷载

f = \frac{q \cdot a^{3}}{E \cdot d^{3}} \cdot C_{f} = \frac{0, 5 \cdot 1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1045 = 0, 006 m

公式 8

以及由内部荷载

f = \frac{Δp \cdot a^{4}}{E \cdot d^{3}} \cdot B_{f} = \frac{0, 180 \cdot 1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1151 = 0, 0022 m

公式 9

这里在被加载的玻璃板上产生的变形为
6,0 mm - 2,2 mm =3,8 mm.

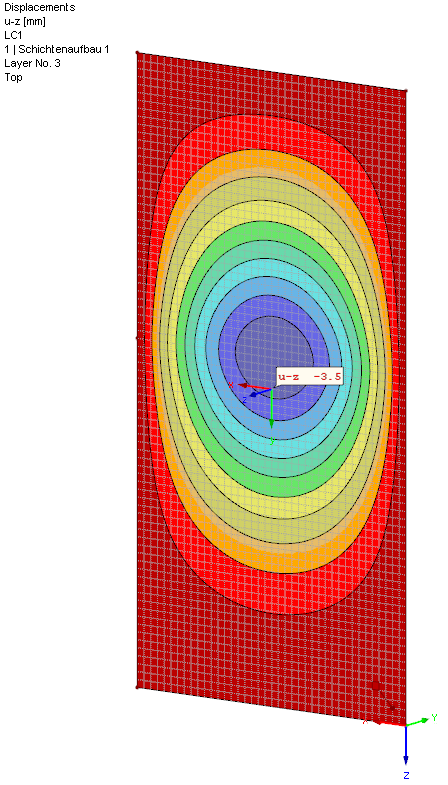
该值与在 RF-GLAS 中的数值计算几乎一致： u_z = 3.5 mm。出现这样的小误差，是由于计算公式是线性的，并且程序是按照第三阶理论以及膜壳影响的应用计算的。

结果变形板 1

结果变形板 1

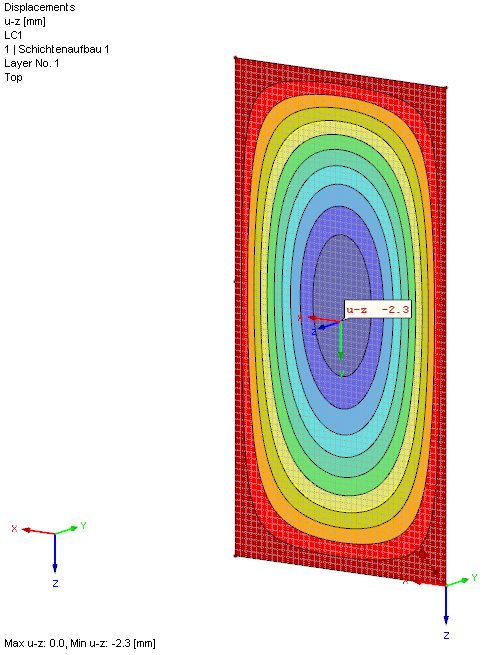
第二个被加载的玻璃板是通过在玻璃之间的气压变形的。由于两块玻璃板的刚度相同，因此该值已经通过 u_z = 2.2 mm 计算得出。

结果变形板 2

结果变形板 2

概述总结

[1]中的计算理论表明，即使是连接的系统也可以手动进行验算。然而随着系统的改变，例如：不同的玻璃厚度、在一个玻璃板面使用 VSG，手动计算就变得越来越复杂。这里与 RF-GLAS 一样的计算机复杂计算为工程师们提供了非常好的帮助。

作者

Lex 先生负责 RFEM 软件的质量保证工作。同时为客户提供技术支持。

链接

玻璃结构设计与计算软件

参考

Feldmeier, F.: Klimabelastung und Lastverteilung bei Mehrscheiben-Isolierglas, Stahlbau 75, Seiten 467 - 478. Berlin: Ernst & Sohn, 2006

下载

RFEM Model File

;