2937x

001527

Dipl.-Ing. (FH) Ulrich Lex

11. Juli 2018

Einfluss einer Linienlast auf eine Isolierglasscheibe

Der Anteil an Glas nimmt bei der Planung eines Gebäudes immer mehr zu. Offene, lichtdurchflutete Gebäude sind ein Zeichen der Moderne. Dies stellt jedoch auch Fachingenieure bei ihrer Planung vor neue Herausforderungen. Raumhohe Glasfassaden, welche zugleich durch einen Handlauf belastet sind, stellen ein solches Beispiel dar. Der Einfluss dieser Belastung sowie die Berechnung der Verformung werden in diesem Beitrag gezeigt.

Berechnungsmodell

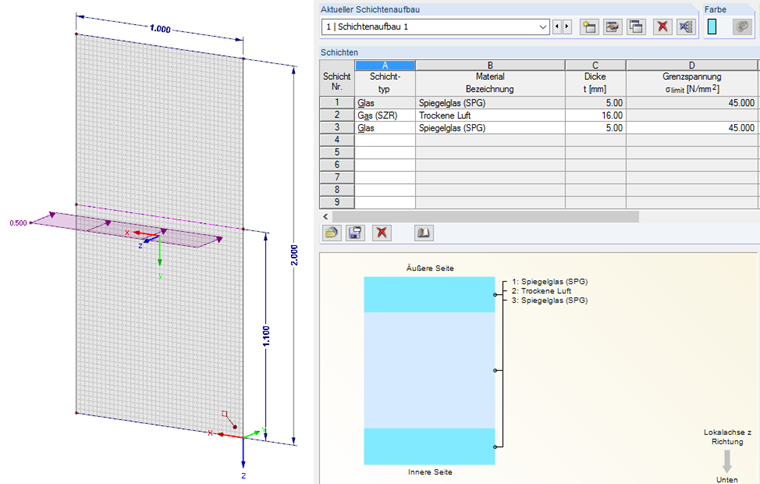
Als Berechnungsmodell wird eine Isolierglasscheibe mit einer Höhe von 2 m und einer Breite von 1 m gewählt. Der Lastangriff der Horizontallast von 0,5 kN liegt bei 1,10 m. Als Scheibenaufbau wurde Isolierglas 5-16-5 gewählt.

System

Verformungsberechnung

Durch das abgeschlossene Volumen des Scheibenzwischenraums ist die Bemessung beider Scheiben nicht ganz trivial. Die Belastung einer Scheibe bewirkt zwangsläufig auf Grund des gekoppelten Systems auch eine Belastung der zweiten Scheibe und somit eine Lastverteilung auf beide Scheiben. Die Größe der Lastverteilung ist jeweils vom gewählten Scheibenaufbau beziehungsweise von der Steifigkeit der Einzelscheiben abhängig.

Üblicherweise wird zur Berechnung von Isoliergläsern ein FEM-Programm (zum Beispiel RFEM, RF-GLAS) herangezogen, welches die statische Problemstellung löst. In [1] sind jedoch auch Formeln zur analytischen Betrachtung abgebildet.

Berechnet man für unser Beispiel die Verformungen händisch, ergeben sich folgende Werte.

Volumenberechnung unter Einheitslast

ν_{p, 1} = ν_{p, 2} = b \cdot h \cdot \frac{a^{4}}{E \cdot d^{3}} \cdot B_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0501 = 0, 01145 \frac{m^{3}}{kN / m^{2}}

Formel 1

ν_{q, 1} = b \cdot h \frac{a^{3}}{E \cdot d^{3}} \cdot C_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0365 = 0, 00834 \frac{m^{3}}{kN / m}

Formel 2

Berechnung Hilfsgrößen

α = α^{} = \frac{ν_{p, 1} \cdot p_{a}}{V_{\Pr}} = \frac{0, 01145 \cdot 100}{1, 0 \cdot 2, 0 \cdot 0, 016} = 35, 78

Formel 3

φ = \frac{1}{1 + α + α^{+}} = \frac{1}{1 + 35, 78 + 35, 78} = 0, 0138

Formel 4

{ΔV}_{ex, 1} = ν_{q, 1} \cdot q_{1} = 0, 00834 \cdot 0, 5 = 0, 00417 m^{2}

Formel 5

{Δp}_{ex} = \frac{{ΔV}_{ex, 1}}{V_{\Pr}} \cdot p_{a} = \frac{0, 00417}{1, 0 \cdot 2, 0 \cdot 0, 016} \cdot 100 = 13, 03 \frac{kN}{m^{2}}

Formel 6

Druck im Scheibenzwischenraum

Δp = φ \cdot ({Δp}_{ex} {Δp}_{c}) = 0, 0138 \cdot (13, 03 0) = 0, 180 \frac{kN}{m^{2}}

Formel 7

Aus diesen Werten lässt sich nun die Durchbiegung in Feldmitte ermitteln.

Aus der Streckenlast

f = \frac{q \cdot a^{3}}{E \cdot d^{3}} \cdot C_{f} = \frac{0, 5 \cdot 1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1045 = 0, 006 m

Formel 8

sowie aus interner Last

f = \frac{Δp \cdot a^{4}}{E \cdot d^{3}} \cdot B_{f} = \frac{0, 180 \cdot 1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1151 = 0, 0022 m

Formel 9

ergibt sich eine resultierende Verformung der belasteten Scheibe von
6,0 mm - 2,2 mm =3,8 mm.

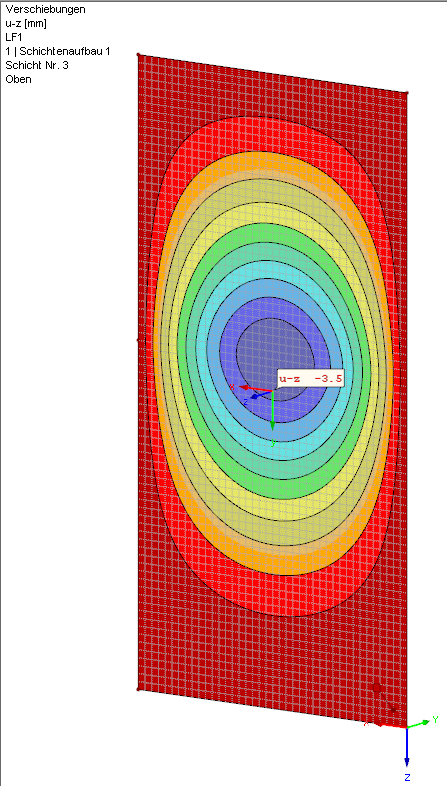
Dieser Wert deckt sich fast exakt mit der numerischen Berechnung von RF-GLAS: u_z = 3,5 mm. Die kleinen Unterschiede treten auf, da die Berechnungsformeln linearisiert sind und das Programm nach Theorie III. Ordnung sowie mit Ansatz einer Membrantragwirkung rechnet.

Ergebnisse Verformung Scheibe 1

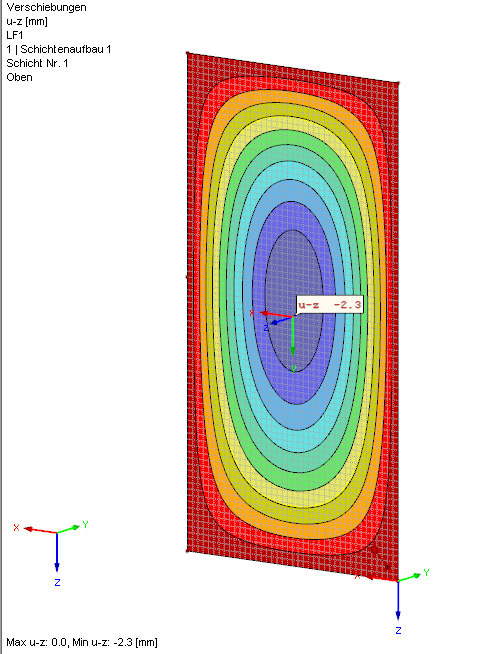
Die sekundär belastete Scheibe wird durch den im SZR vorherrschenden Gasdruck verformt. Da beide Scheiben dieselbe Steifigkeit besitzen, wurde dieser Wert bereits zuvor mit u_z = 2,2 mm berechnet.

Ergebnisse Verformung Scheibe 2

Fazit

Der Berechnungsansatz von [1] zeigt, dass es möglich ist, selbst gekoppelte Systeme noch von Hand zu überprüfen. Mit Veränderung des Systems, zum Beispiel unterschiedliche Scheibendicken oder sogar der Verwendung von VSG auf einer Scheibenseite, wird die Handrechnung jedoch immer komplizierter. Hierbei bietet eine rechnergestützte Berechnung wie mit RF-GLAS eine sehr gute Hilfestellung und Erleichterung für den planenden Ingenieur.

Autor

Herr Lex betreut die Entwicklung im Glasbau und sorgt für die Qualitätssicherung des Programms RFEM. Zudem ist er im Kundensupport aktiv.

Links

Statiksoftware für den Glasbau

Referenzen

Feldmeier, F.: Klimabelastung und Lastverteilung bei Mehrscheiben-Isolierglas, Stahlbau 75, Seiten 467 - 478. Berlin: Ernst & Sohn, 2006

Downloads

RFEM-Modelldatei

2,47 MB

;