2938x

001527

mgr inż. (FH) Ulrich Lex

2018-07-11

Wpływ obciążenia liniowego na szybę zespoloną

Wzrasta udział szkła w projektowaniu budynku. Otwarte, pełne światła budynki są charakterystyczne dla współczesnej architektury. Wyspecjalizowani inżynierowie muszą jednak stawić czoła nowym wyzwaniom podczas planowania. Jednym z przykładów są szklane fasady sięgające sufitu, obciążone poręczą. W artykule przedstawiono wpływ tego obciążenia oraz obliczenia odkształcenia.

Model obliczeniowy

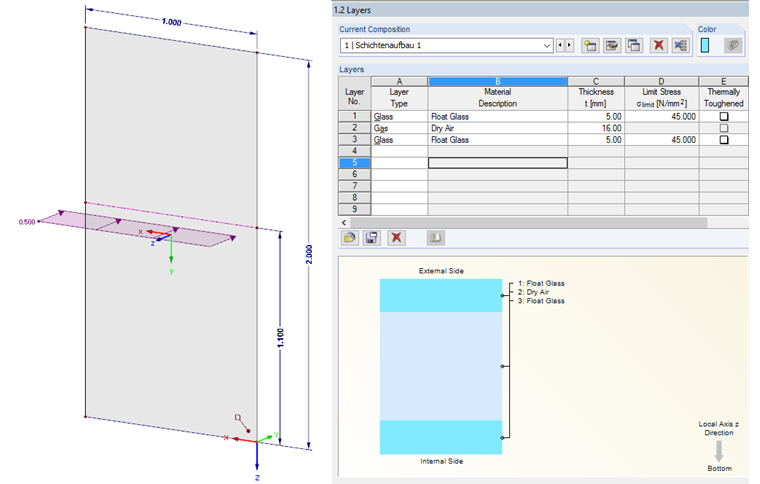
Za model analityczny służy szyba zespolona o wysokości 2 m i szerokości 1 m. Liniowe obciążenie poziome o wartości 0,5 kN/m przyłożono na wys.1,10 m. Jako konstrukcję szybową zostało wybrane szkło izolacyjne 5-16-5.

Konstrukcja

Analiza deformacji

Ponieważ przestrzeń międzyszybowa jest zamknięta, wymiarowanie obu szyb jest złożone. Obciążenie jednej szyby nieuchronnie powoduje również obciążenie drugiej szyby, a tym samym rozkład obciążenia na obie szyby. Zasięg rozmieszczenia obciążenia zależy od wybranej konstrukcji szyby lub od sztywności pojedynczych szyb.

Oprogramowanie MES (takie jak RFEM lub RF-GLASS) jest zwykle używane do analizy szkła izolacyjnego, co rozwiązuje problem konstrukcyjny. Jednak wzory dla widoku analitycznego pokazano również w [1].

Poniższe wzory odnoszą się do obliczeń ręcznych.

Obliczenia bryły pod obciążeniem jednostkowym

u_{p, 1} = u_{p, 2} = b \cdot h \cdot \frac{a^{4}}{E \cdot d^{3}} \cdot B_{v} = 1.0 \cdot 2.0 \cdot \frac{1 . 0^{4}}{7 \cdot 10^{7} \cdot 0 . 005^{3}} \cdot 0.0501 = 0.01145 \frac{m^{3}}{kN / m^{2}}

Wzór 1

u_{q, 1} = b \cdot h \frac{a^{3}}{E \cdot d^{3}} \cdot C_{v} = 1.0 \cdot 2.0 \cdot \frac{1 . 0^{3}}{7 \cdot 10^{7} \cdot 0 . 005^{3}} \cdot 0.0365 = 0.00834 \frac{m^{3}}{kN / m}

Wzór 2

Obliczenia wartości pomocniczych

α = α^{} = \frac{u_{p, 1} \cdot p_{a}}{V_{\Pr}} = \frac{0.01145 \cdot 100}{1.0 \cdot 2.0 \cdot 0.016} = 35.78

Wzór 3

Error converting from LaTeX to MathML

Wzór 4

{ΔV}_{ex, 1} = u_{q, 1} \cdot q_{1} = 0.00834 \cdot 0.5 = 0.00417 m^{2}

Wzór 5

{Δp}_{ex} = \frac{{ΔV}_{ex, 1}}{V_{\Pr}} \cdot p_{a} = \frac{0.00417}{1.0 \cdot 2.0 \cdot 0.016} \cdot 100 = 13.03 \frac{kN}{m^{2}}

Wzór 6

Ciśnienie w przestrzeni międzyszybowej

Δp = φ \cdot ({Δp}_{ex} {Δp}_{c}) = 0.0138 \cdot (13.03 0) = 0.180 \frac{kN}{m^{2}}

Wzór 7

Na podstawie tych wartości można teraz określić ugięcie w połowie rozpiętości.

Z rozmieszczonego obciążenia

f = \frac{q \cdot a^{3}}{E \cdot d^{3}} \cdot C_{f} = \frac{0.5 \cdot 1 . 0^{3}}{7 \cdot 10^{7} \cdot 0 . 005^{3}} \cdot 0.1045 = 0.006 m

Wzór 8

jak również z obciążenia wewnętrznego

f = \frac{Δp \cdot a^{4}}{E \cdot d^{3}} \cdot B_{f} = \frac{0.180 \cdot 1 . 0^{4}}{7 \cdot 10^{7} \cdot 0 . 005^{3}} \cdot 0.1151 = 0.0022 m

Wzór 9

powstaje odkształcenie wypadkowe obciążonej szyby
6,0 mm - 2,2 mm =3,8 mm.

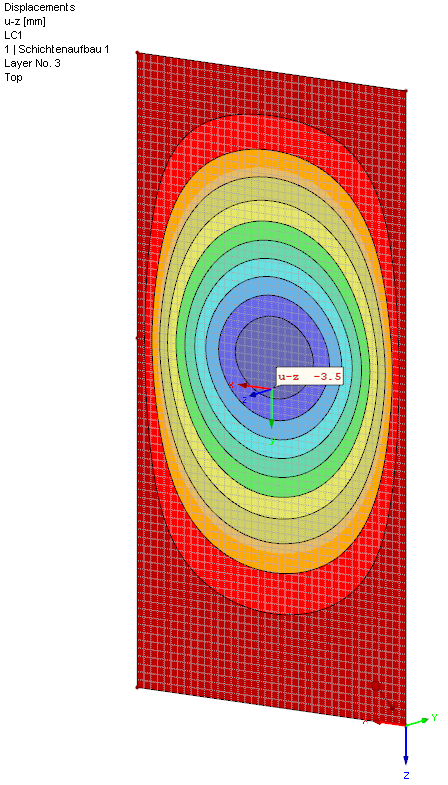
Wartość niemal dokładnie odpowiada obliczeniom numerycznym w RF-GLASS: _uz = 3,5 mm. Niewielkie różnice występują, ponieważ wzory obliczeń są linearyzowane, a program przeprowadza obliczenia zgodnie z teorią dużych deformacji i wykorzystuje podejście oparte na nośności membrany.

Wyniki odkształcenia szyby 1

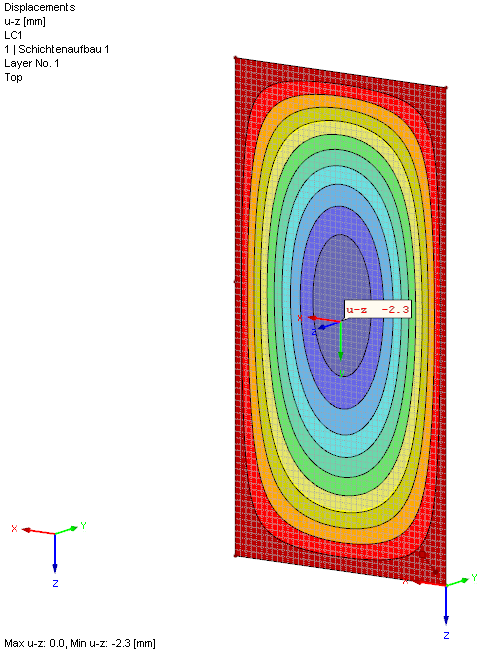
Wtórnie obciążona szyba jest odkształcona przez działanie ciśnienia gazu, znajdującego się w przestrzeni międzyszybowej. Ponieważ obie szyby mają tę samą sztywność, wartość ta została już obliczona przy u_z = 2,2 mm.

Wyniki odkształcenia szyby 2

Wniosek

Teoria obliczeń [1] pokazuje, że możliwe jest ręczne sprawdzanie nawet połączonych systemów. Obliczenia ręczne stają się bardziej złożone, kiedy do układu wprowadzane zostaną zmiany, na przykład różne grubości szyby lub szkło klejone po jednej stronie szyby. Obliczenia wspomagane komputerowo, na przykład za pomocą modułu RF-GLASS, stanowią dla inżyniera duże wsparcie i ułatwienie.

Autor

Pan Lex jest odpowiedzialny za rozwój produktów dla konstrukcji szklanych oraz za zapewnienie jakości programu RFEM. Zapewnia również wsparcie techniczne dla naszych klientów.

Odnośniki

Obliczanie konstrukcji szklanych

Odniesienia

Feldmeier, F.: Klimabelastung und Lastverteilung bei Mehrscheiben-Isolierglas, Stahlbau 75, Seiten 467 - 478. Berlin: Ernst & Sohn, 2006

Pobrane

Plik modelu w RFEM

2,47 MB

;