Modèle de calcul
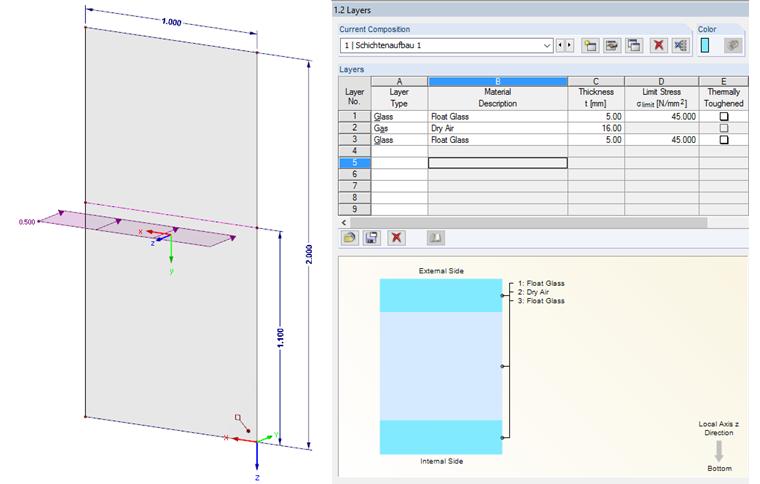
Le modèle d’analyse est un vitrage isolant d’une hauteur de 2 m et d’une largeur de 1 m. La charge horizontale de 0,5 kN est appliquée sur 1,10 m. Le vitrage isolant 5-16-5 a été choisi comme structure de vitrage.
Calcul des déformations
La vérification des deux vitrages est complexifiée par le solide contenu entre eux. Le chargement d'une vitre entraîne inévitablement la charge de la deuxième vitre en raison du système couplé et, par conséquent, une distribution de charge sur les deux vitres. La taille de la distribution de charge dépend de la structure de vitrage sélectionnée ou de la rigidité des vitrages individuels.Les logiciels d’analyse aux éléments finis (tels que RFEM ou RF-GLASS) sont généralement utilisés pour analyser le verre isolant, ce qui permet de résoudre le problème structurel. Cependant, des formules pour la vue analytique sont également présentées dans [1].
Les valeurs suivantes sont les résultats si les déformations sont calculées manuellement pour cet exemple.
Calcul d’un solide sous charge unitaire
Calcul des quantités auxiliaires
Error converting from LaTeX to MathML
Pression dans l’espace entre deux vitrages
Il est maintenant possible de déterminer la flèche à mi-travée à partir de ces valeurs.
À partir de la charge uniformément distribuée
ainsi que la charge interne
résulte une déformation résultante de la vitre chargée de
6,0 mm - 2,2 mm = 3,8 mm.
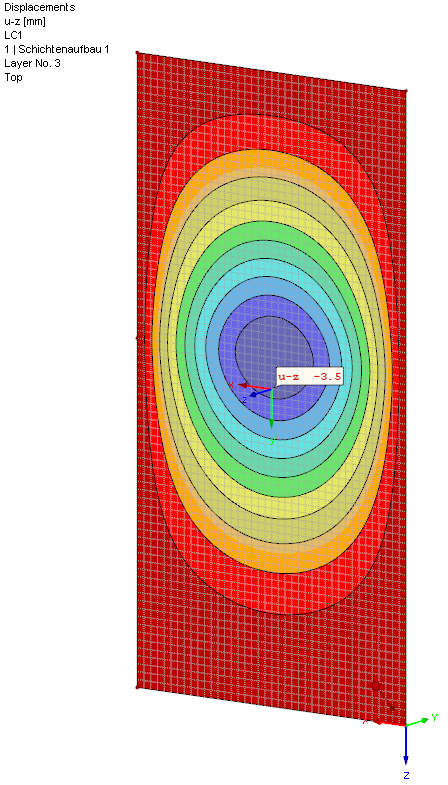
Cette valeur correspond presque exactement au calcul numérique de RF-GLASS : uz = 3,5 mm. De légères différences surviennent car les formules de calcul sont linéarisées et le logiciel calcule selon la théorie des grandes déformations et utilise une approche de la capacité portante de la membrane.
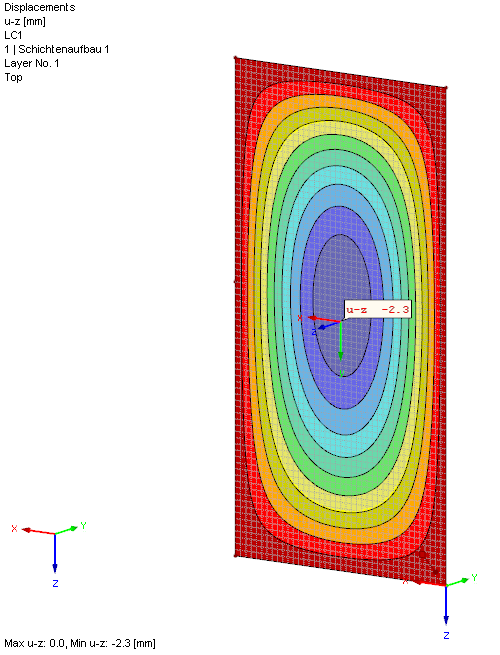
Le vitrage secondaire chargé est déformé par la pression de gaz dominante dans l’espace entre vitrages. Comme les deux vitres ont la même rigidité, cette valeur a déjà été calculée avec uz = 2,2 mm.
