2938x

001527

Dipl.-Ing. (FH) Ulrich Lex

11.7.2018

Vliv liniového zatížení na izolační sklo

Podíl prosklení se při projektování budov neustále zvyšuje. Otevřené a světlem zalité budovy jsou charakteristickým znakem moderního stavitelství. To ovšem také přináší nové výzvy pro projektanty. Příkladem jsou celoplošné skleněné fasády, které jsou současně zatíženy madlem. Vliv takového zatížení si spolu s výpočtem deformace ukážeme v našem příspěvku.

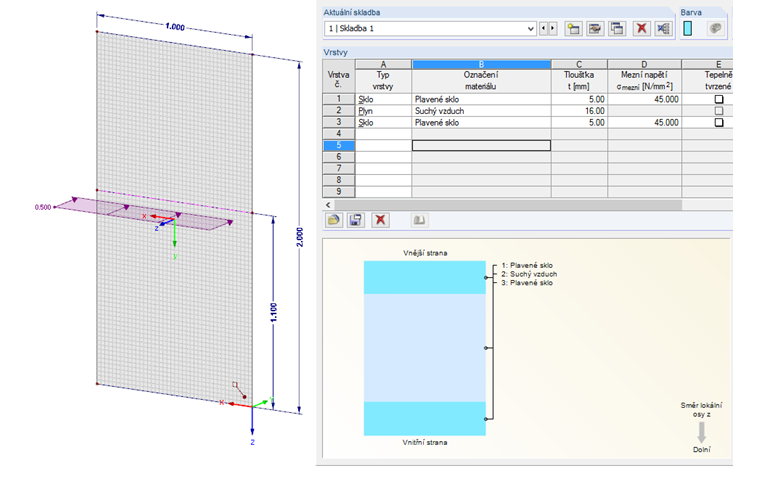
Výpočetní model

Jako model pro posouzení nám poslouží tabule z izolačního skla o výšce 2 m a šířce 1 m. Vodorovné zatížení o velikosti 0,5 kN působí ve výšce 1,10 m. Pro izolační sklo jsme zvolili skladbu 5-16-5.

Konstrukce

Výpočet deformací

Kvůli uzavřenému objemu meziskelního prostoru není posouzení obou tabulí úplně jednoduché. Zatížení jedné tabule nutně vyvolává ve spojeném systému zatížení i na druhou tabuli, a zatížení se tak rozděluje na obě tabule. Rozdělení zatížení pak závisí vždy na zvolené skladbě izolačního skla, respektive na tuhosti jednotlivých tabulí.

Obvykle k výpočtu izolačních skel a posouzení statiky používáme program pro výpočty metodou konečných prvků (například RFEM, RF-GLASS). V [1] se uvádí ovšem také vzorce pro analytickou metodu posouzení.

Při ručním výpočtu deformací v našem příkladu dospějeme k následujícím hodnotám.

Výpočet objemu při jednotkovém zatížení

ν_{p, 1} = ν_{p, 2} = b \cdot h \cdot \frac{a^{4}}{E \cdot d^{3}} \cdot B_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0501 = 0, 01145 \frac{m^{3}}{kN / m^{2}}

Vzorec 1

ν_{q, 1} = b \cdot h \frac{a^{3}}{E \cdot d^{3}} \cdot C_{v} = 1, 0 \cdot 2, 0 \cdot \frac{1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 0365 = 0, 00834 \frac{m^{3}}{kN / m}

Vzorec 2

Výpočet pomocných veličin

α = α^{} = \frac{ν_{p, 1} \cdot p_{a}}{V_{\Pr}} = \frac{0, 01145 \cdot 100}{1, 0 \cdot 2, 0 \cdot 0, 016} = 35, 78

Vzorec 3

Error converting from LaTeX to MathML

Vzorec 4

{ΔV}_{ex, 1} = ν_{q, 1} \cdot q_{1} = 0, 00834 \cdot 0, 5 = 0, 00417 m^{2}

Vzorec 5

{Δp}_{ex} = \frac{{ΔV}_{ex, 1}}{V_{\Pr}} \cdot p_{a} = \frac{0, 00417}{1, 0 \cdot 2, 0 \cdot 0, 016} \cdot 100 = 13, 03 \frac{kN}{m^{2}}

Vzorec 6

Tlak v meziskelním prostoru

Δp = φ \cdot ({Δp}_{ex} {Δp}_{c}) = 0, 0138 \cdot (13, 03 0) = 0, 180 \frac{kN}{m^{2}}

Vzorec 7

Na základě těchto hodnot lze nyní stanovit průhyb ve středu pole.

Ze spojitého zatížení

f = \frac{q \cdot a^{3}}{E \cdot d^{3}} \cdot C_{f} = \frac{0, 5 \cdot 1, 0^{3}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1045 = 0, 006 m

Vzorec 8

a z vnitřního zatížení

f = \frac{Δp \cdot a^{4}}{E \cdot d^{3}} \cdot B_{f} = \frac{0, 180 \cdot 1, 0^{4}}{7 \cdot 10^{7} \cdot 0, 005^{3}} \cdot 0, 1151 = 0, 0022 m

Vzorec 9

se určí výsledná deformace zatěžované tabule
6,0 mm - 2,2 mm = 3,8 mm.

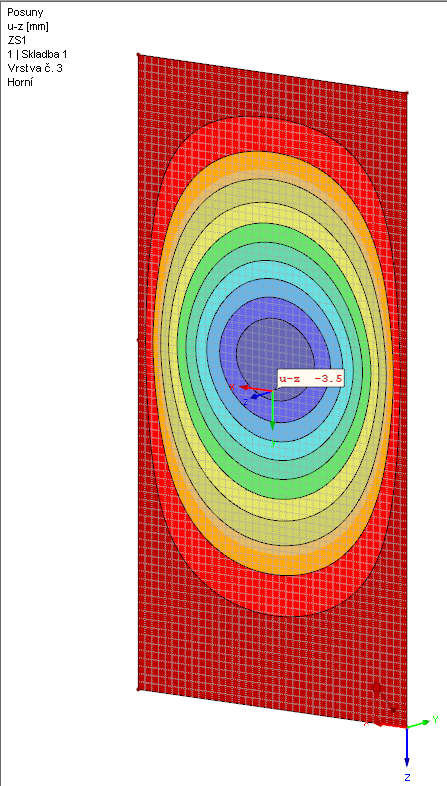
Tato hodnota odpovídá téměř přesně výsledku numerického výpočtu v modulu RF-GLASS: u_z = 3,5 mm. Malé rozdíly plynou z linearizace výpočetních vzorců a dále z uplatnění výpočtu třetího řádu a uvažování nosnosti membrány v programu.

Výsledná deformace u tabule 1

Druhotně zatížená tabule se deformuje vlivem dominantního tlaku plynu působícího v meziskelním prostoru. Vzhledem k tomu, že obě tabule mají stejnou tuhost, byla již dříve stanovena tato hodnota na u_z = 2,2 mm.

Výsledná deformace u tabule 2

Závěr

Výpočet podle [1] ukazuje, že i spojené systémy lze ověřit ručně. Pokud však systém upravíme, například použijeme tabule o rozdílné tloušťce anebo dokonce vrstvené bezpečnostní sklo na jedné straně, ruční výpočet se zkomplikuje. V takovém případě přináší statikovi výpočetní modul RF-GLASS vítanou pomoc a usnadňuje mu práci.

Autor

Ing. Lex je zodpovědný za vývoj produktů pro skleněné konstrukce a za zajištění kvality programu RFEM. V rámci technické podpory pečuje o zákazníky.

Odkazy

Statické výpočty a navrhování skleněných konstrukcí

Reference

Feldmeier, F.: Klimabelastung und Lastverteilung bei Mehrscheiben-Isolierglas, Stahlbau 75, Seiten 467 - 478. Berlin: Ernst & Sohn, 2006

Stahování

Model v programu RFEM

2,47 MB

;