20821x

001563

Алекс Бэкон, EIT

2019-03-13

Расчет железобетонных балок по ACI 318-14 в программе RFEM

С помощью модуля RF-CONCRETE Members мы можем выполнить расчет железобетонной балки по норме ACI 318-14. Для обеспечения надежности конструкции важен точный расчет бетонной балки на растяжение и сжатие, а также расчет поперечного армирования. В следующей статье будет подтвержден расчет арматуры в стержнях RF-CONCRETE с помощью пошаговых аналитических уравнений в соответствии со стандартом ACI 318-14, включая прочность на момент, прочность на сдвиг и требуемую арматуру. Приведенный пример железобетонной балки с двухслойной арматурой, включая арматуру, работающую на сдвиг, будет рассчитан на предельное состояние по несущей способности (ULS).

Описание

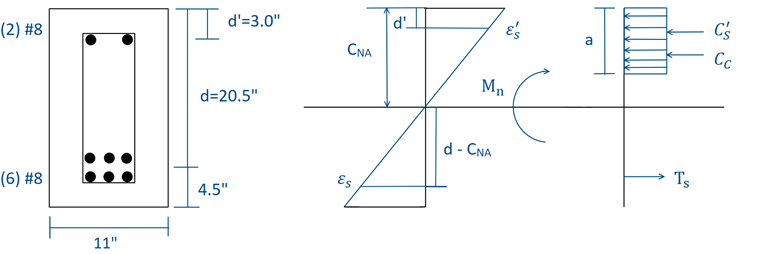
Сечение железобетонной балки с двухслойной арматурой, представленное на рисунке 01, будет рассчитано на предельную несущую способность по ACI 318-14 [1] с применением расчетных сочетаний нагрузок LRFD. На балку действуют равномерная постоянная нагрузка без коэффициента и временная нагрузка 2,0 kip/ft и 3,2 kip/ft соответственно. Выбранная прямоугольная балка имеет внешнее сечение 25 дюймов ⋅ 11 дюймов. Данный материал (бетон) имеет прочность на сжатие (f'_c), равную 5000 psi (фунтов на кв. дюйм), а арматурная сталь имеет предел текучести (f_y), равный 60 000 psi. The compression reinforcement (A'_s) consists of two #8 bars with a centroid distance (d') of 3.0 inches from the top compression fiber with a total area of 1.57 in². The tensile reinforcement (A_s) consists of six #8 bars with a centroid distance (d) of 20.5 inches from the top compression fiber with a total area of 4.71 in². Арматура, работающая на сдвиг (A_v), представляет собой хомуты №4 общей площадью 0,4 кв. дюйма. Размеры и диаграмма напряжений и деформаций сечения балки показаны на рисунке 01.

Железобетонное сечение: диаграмма напряжений и деформаций

Stahlbetonquerschnitt: Spannungs-Dehnungs-Diagramm

Прочность момента

Требуемый номинальный момент M_u от прилагаемых нагрузок составляет 4512,00 kip-in. Для выведения уравнения нахождения номинального момента нам потребуются следующие допущения.

Сжатая арматура не достигает предела: ε'_s < ε_y → f'_s = E_s ⋅ ε'_s
Растянутая арматура достигает: ε_s ≥ ε_y → f_s = f_y

С помощью уравнения, приведенного ниже, мы можем определить нейтральную ось, а затем проанализировать диаграмму напряжений и деформаций балки. Уравнение получено путем задания сил сжатия, равных растягивающим силам, для достижения равновесия:
T_s = C'_s + C_c → A_s ⋅ f_y - A'_s ⋅ f'_s - 0.85 ⋅ f'_c ⋅ a ⋅ b = 0

Применив диаграмму деформаций и подобные треугольники, мы можем предположить, что:

ε'_{s} = \frac{ε_{cu} \cdot (c_{NA} - d')}{c_{NA}}

Формула 1

Мы также знаем, что: a = β₁ ⋅ C_NA

Substituting β₁ ⋅ C_NA and

ε'_{s} = \frac{ε_{cu} \cdot (c_{NA} - d')}{c_{NA}}

Формула 1

for a and ε'_s, respectively, into the equilibrium equation above, the neutral axis can be calculated, as all values are known except C_NA.

A_{s} \cdot f_{y} - \frac{A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot (C_{NA} - d')}{C_{NA}} - 0.85 \cdot f'_{c} \cdot β_{1} \cdot C_{NA} \cdot b = 0

Формула 2

Using Table 22.2.2.4.3 from ACI 318 - 14 [1], β₁ is equal to 0.80. Решив уравнение с CNA, мы получим, что оно находится на расстоянии около 15 см от верхнего предельно сжатого слоя.

Данные допущения (1 и 2) необходимо проверить. Допущение 1 заключается в расчете деформации сжатой арматуры (ε'_s) и ее сопоставлении с деформацией текучести (ε_y). Если ε'_s меньше, чем ε_y, то наше предположение верно. Допущение 2 заключается в расчете деформации растянутой стальной арматуры (ε_s) и ее сравнении ее ε_y. Если ε_s больше, чем ε_y, то наше предположение верно. С помощью расчета мы убедимся (не показано в статье), что допущения 1 и 2 верны.

Наконец, для определения номинального момента (M_n) мы зададим сумму моментов в месте сжатого бетона (C_c) равной нулю. Это показано на диаграмме рисунка 01.

Уравнение имеет следующий вид:

M_{n} = C'_{s} \cdot (\frac{a}{2} - d') + T_{s} \cdot (d - \frac{a}{2})

Формула 3

Before we can solve for M_n, we must substitute C'_s and T_s for

A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot \frac{(C_{NA} - d')}{C_{NA}}

Формула 4

and A_s ⋅ f_y, respectively.

Уравнение имеет следующий вид:

M_{n} = A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot \frac{(C_{NA} - d')}{C_{NA}} \cdot (\frac{a}{2} - d') + A_{s} \cdot f_{y} \cdot (d - \frac{a}{2})

Формула 5

Мы также должны вычислить значение a, умножив β₁ на C_NA,перед расчетом M_n.

a = 4,66 дюйма

Подставляя полученные значения в уравнение M_n, мы получим следующее:

M_{n} = 1.57 \cdot 29, 000 \cdot \frac{0.003 \cdot (5.83 - 2.5)}{5.83} \cdot (\frac{4.66}{2} - 3.0) + 4.71 \cdot 60 \cdot (20.5 - \frac{4.66}{2})

Формула 6

Mn будет равно 5122,69 kip-in.

Наконец, коэффициент надежности (φ) определим по таблице 21.2.2 нормы ACI 318 -14 [1]. Для вычисления φ деформация при растяжении сравнивается с предельной деформацией, равной 0,005. ε_t равно 0,00755 и больше 0,005. Для балки решающей является деформация при растяжении. По таблице 21.2.2 φ равен 0,90. При умножении полученного коэффициента на M_n мы получим φM_n равное 4610,42 kip-in. Таким образом, несущая способность балки достаточна для приложенного изгибающего момента.

φM_n > M_u = 4512.00 kip-in o.k.

Прочность на сдвиг

Внимание! Полезная высота (d) для расчета на сдвиг будет принята равной 22,5 дюйма, в отличие от 20,5 дюймов, указанных в условии задачи. Точка приложения максимальной силы сдвига также является точкой минимального изгибающего момента (лицевая сторона опоры). Для приведения аналитических вычислений в соответствие с расчетом арматуры в модуле RF-CONCRETE Members, эффективная высота балки в модуле задана на основе количества требуемой растянутой арматуры, а не рассчитанной растянутой арматуры. Это значит, что при минимальном изгибающем моменте на опорной поверхности при расчетной высоте 60 см, требуется только один слой растянутой арматуры.

На основе п. 22.5.1.1 [1], we calculate the nominal shear strength (V_n) of the beam. Для расчета на сдвиг применяется следующее уравнение:
V_n = φ ⋅ (V_c + V_s)

Referencing Table 22.5.5.1 [1], concrete shear strength V_c is equal to the minimum of equations a, b, and c calculated in Sections 1, 2, and 3 below.

1. Уравнение a имеет следующий вид:

V_{c - a} = (1.9 \cdot λ \cdot \sqrt{f'_{c}} 2, 500 \cdot ρ_{w} \cdot \frac{V_{u} \cdot d}{M_{u}}) \cdot b_{w} \cdot d, with λ = 1

Формула 7

Mu достигается при Vu на расстоянии d от поверхности опоры (раздел 9.4.3.2 [1]). Таким образом, M_u равно 1533,38 kip-in. V_u = 61,10 kips.

ρ_{w} = \frac{A_{s}}{b_{w} \cdot d} = 0.01992

Формула 8

V_ca = 44,96 kips.

2. Уравнение b имеет следующий вид:

V_{c - b} = (1.9 \cdot λ \cdot \sqrt{f'_{c}} 2, 500 \cdot ρ_{w}) \cdot b_{w} \cdot d

Формула 9

V_cb = 46,26 kips.

3. Уравнение c имеет следующий вид:

V_{c - c} = 3.5 \cdot λ \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d

Формула 10

V_cc = 61,25 kips.

Таким образом, выбрав минимальное значение из вышеприведенных уравнений, мы получим, что V_c равно 44,96 kips (тыс. фунтов на кв. дюйм).

После расчета бетона на номинальный сдвиг определим минимальное поперечное армирование в соответствии с п. 9.6.3 [1]. Here, if the required shear strength V_u is less than 0.5 ⋅ φ ⋅ V_c, then shear reinforcement is required.

V_u < 0.5 ⋅ φ ⋅ V_c
где
φ = 0,75 (по таблице 21.2.1 [1])

Therefore, V_u = 61.10 kips > 16.86 kips. Stirrups are required.

Расчетный шаг арматуры определим согласно п. 9.5.1.1 [1]:
φ ⋅ V_n > V_u

We substitute (V_c + V_s) for V_n.

V_{s} > \frac{V_{u} - ϕ \cdot V_{c}}{ϕ}

Формула 11

S_o, V_s > 36.51 kips.

Из гл. 22.5.10.5.3 [1], для расчета требуемой прочности арматуры на сдвиг мы применим следующее уравнение:

V_{s} = \frac{A_{v} \cdot f_{yt} \cdot d}{s}

Формула 12

Где fyt - предел текучести стальной растянутой арматуры, а d - расстояние от верхнего сжатого слоя до центра тяжести растянутой арматуры.

Максимальный шаг был рассчитан как 14,79 дюйма. При этом шаг арматуры, работающей на сдвиг, равен 14 дюймов. Using a spacing of s = 14 inches, the above equation for steel shear strength, V_s, is calculated to be 38.57 kips.

По таблице 9.7.6.2.2 [1] мы определим максимальный шаг армирования. Нужно решить следующее уравнение для того, чтобы определить, какое уравнение из таблицы 9.7.6.2.2 применимо в нашем случае:

4 \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d = 4 \cdot \sqrt{5, 000 psi} \cdot 11 in \cdot 22.5 in = 70.29 kips

Формула 13

The steel shear strength, V_s = 38.57 kips, is less than the calculated value of 70.00 kips. Referencing Table 9.7.6.2.2, the maximum shear spacing can be determined using the minimum value from the following calculations:

s_{\max} = \min (24, \frac{d}{2})

Формула 14

Максимальный шаг равен 11,25 дюйма. Шаг арматуры, определенный ранее для стержней №4, расположенных через 14 дюймов, недостаточен, вместо него следует применить размер 11 дюймов. Необходимо убедиться, что несущая способность при сдвиге больше, чем требуемая максимальная прочность на сдвиг, для того, чтобы быть уверенным, что шаг и арматура, работающая на сдвиг, отвечают требованиям. With respect to our new max spacing of 11 inches, we receive a V_s value of 49.09 kips.

V_n = φ ⋅ (V_c + V_s) = 0.75 ⋅ (44.96 + 49.09) > V_u= 61.10 kips

Vn = 70,54 > 61,10 kips

Для окончательной проверки расчета мы проверим правильность размеров сечения согласно п. 22.5.1.2. [1]. Для этого предел прочности на сдвиг сравнивается с уравнением 22.5.1.2 из ACI 318-14 [1]:

V_{u} ⩽ ϕ \cdot (V_{c} 8 \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d)

Формула 15

Данное значение равно 105,04 kips и больше, чем V_u. Таким образом, заданные размеры сечения достаточны.

Результаты

Вместо расчета армирования бетона вручную мы может применить дополнительный модуль RF-/CONCRETE Members и выполнить расчет по норме ACI 318-14 [1]. Данный модуль определит требуемую арматуру в соответствии с приложенными к балке нагрузками. Кроме того, программа рассчитает существующую арматуру на основе размеров стержней, заданных пользователем, с учетом требований к шагу арматуры по норме. Пользователь имеет возможность внести небольшие изменения в предоставленный расчет арматуры с помощью таблицы результатов.

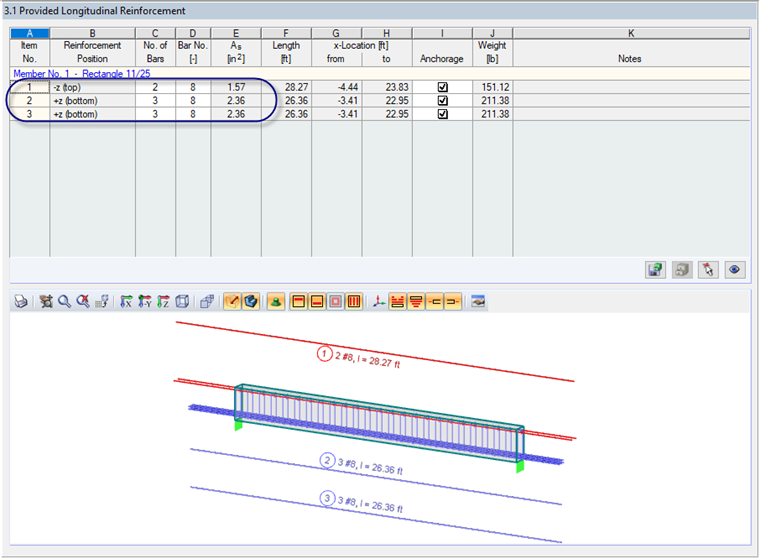
Based on the applied loads for this example, RF-CONCRETE Members has determined a required minimum tension reinforcement of 4.46 in² and a provided reinforcement of (6) #8 bars (A_s = 4.72 in²). This reinforcement layout is shown in Figure 02.

Диаграмма растяжения и сжатия арматуры в RFEM

Zug- und Druckbewehrung RFEM-Diagramm

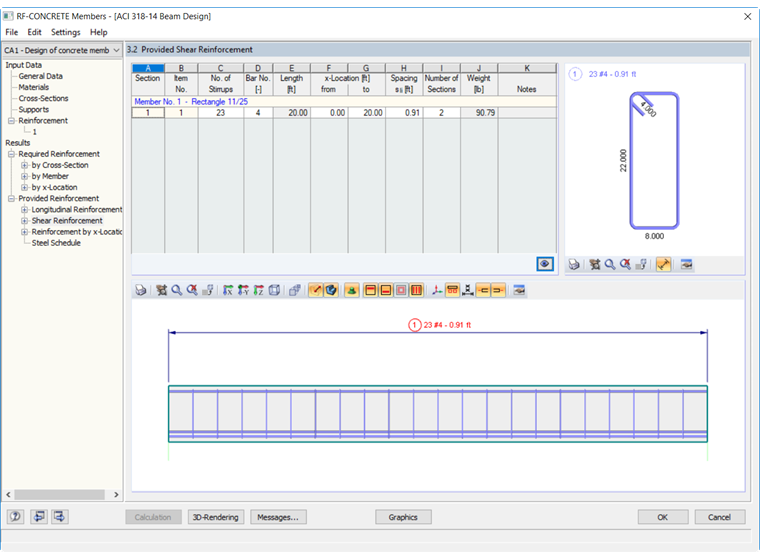
Требуемая работающая на сдвиг арматура для стержня в RF-CONCRETE Members была рассчитана равной 0,41 in²/ft. Для того, чтобы достичь этой минимальной площади и обеспечить равномерный шаг хомутов по всей длине 6-метровой балки, программа рекомендует использовать стержни №4 с шагом 10,91 дюйма. Схема арматуры, работающей на сдвиг, показана на рисунке 03.

Bügelbewehrung RFEM-Diagramm

Автор

Алекс отвечает за обучение клиентов, техническую поддержку и за разработку наших программ для североамериканского рынка.

Ссылки

Программы для расчёта и проектирования железобетонных конструкций

Ссылки

ACI 318-14, Требования строительных норм и правил к конструкционному бетону и комментарий

Скачивания

Модель в RFEM

1,35 MB

;