20820x

001563

Alex Bacon, EIT

2019-03-13

Wymiarowanie belek z betonu zbrojonego zgodnie z ACI 318-14 w RFEM

Przy użyciu prętów RF-CONCRETE Members możliwe jest wymiarowanie belek betonowych zgodnie z ACI 318-14. Dokładne obliczenie zbrojenia na rozciąganie, ściskanie i ścinanie belki betonowej jest ważne ze względów bezpieczeństwa. Poniższy artykuł potwierdzi obliczenia zbrojenia w RF-CONCRETE Members przy użyciu równań analitycznych krok po kroku zgodnie z normą ACI 318-14, w tym wytrzymałości na zginanie, ścinanie i wymagane zbrojenie. Analizowany przykład belki podwójnie zbrojonej betonu zawiera zbrojenie na ścinanie i zostanie zaprojektowany w stanie granicznym nośności (SGN).

Opis

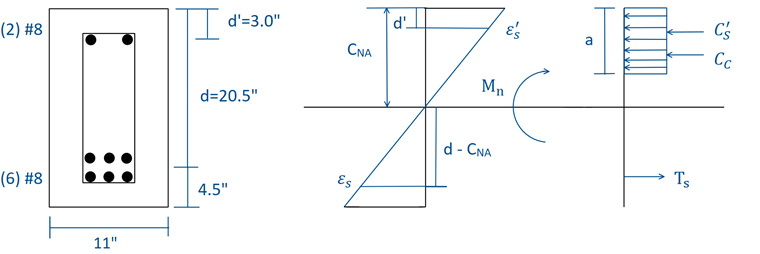
Przekrój dwubelkowy pokazany na rysunku 01 zostanie obliczony zgodnie z SGN zgodnie z ACI 318-14 [1] przy użyciu obliczeniowych kombinacji obciążeń LRFD. Do belki przyłożone są stałe obciążenia stałe i zmienne o wartości odpowiednio 2,0 kip/ft i 3,2 kip/ft. Wybrana belka prostokątna ma całkowity przekrój 25 cali 11 cali. Beton ma wytrzymałość na ściskanie (f'_c ) 5 000 psi, podczas gdy stal zbrojeniowa ma granicę plastyczności (_fy ) 60.000 psi. The compression reinforcement (A'_s) consists of two #8 bars with a centroid distance (d') of 3.0 inches from the top compression fiber with a total area of 1.57 in². The tensile reinforcement (A_s) consists of six #8 bars with a centroid distance (d) of 20.5 inches from the top compression fiber with a total area of 4.71 in². The shear reinforcement (A_v) includes #4 stirrups for a total area of 0.4 in². Wymiary i wykres naprężenie/odkształcenie przekroju belki pokazano na rysunku 01.

Przekrój betonu zbrojonego: Wykres naprężenia i odkształcenia

Stahlbetonquerschnitt: Spannungs-Dehnungs-Diagramm

Wytrzymałość na zginanie

The required nominal moment, M_u, from the applied loads is found to be 4512.00 kip-in. Wyprowadzenie równania w celu znalezienia momentu nominalnego wymaga następujących założeń.

Stal ściskana nie ulega uplastycznieniu: ε'_s < ε_y → f'_s = E_s ⋅ ε'_s
Stal rozciągana plasuje się następująco: ε_s ≥ ε_y → f_s = f_y

Analizując wykres naprężeń i odkształceń belki, oś obojętną można znaleźć za pomocą poniższego równania. Równanie uzyskuje się poprzez ustalenie sił ściskających równych siłom rozciągającym, w celu zachowania równowagi:
T_s = C'_s + C_c → A_s ⋅ f_y - A'_s ⋅ f'_s - 0.85 ⋅ f'_c ⋅ a ⋅ b = 0

Korzystając z wykresu odkształceń i podobnych trójkątów, możemy założyć:

ε'_{s} = \frac{ε_{cu} \cdot (c_{NA} - d')}{c_{NA}}

Wzór 1

Wiemy również: a = β₁ ⋅ C_NA

Substituting β₁ ⋅ C_NA and

ε'_{s} = \frac{ε_{cu} \cdot (c_{NA} - d')}{c_{NA}}

Wzór 1

for a and ε'_s, respectively, into the equilibrium equation above, the neutral axis can be calculated, as all values are known except C_NA.

A_{s} \cdot f_{y} - \frac{A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot (C_{NA} - d')}{C_{NA}} - 0.85 \cdot f'_{c} \cdot β_{1} \cdot C_{NA} \cdot b = 0

Formuła 2

Using Table 22.2.2.4.3 from ACI 318 - 14 [1], β₁ is equal to 0.80. Obliczając CNA, okazuje się, że jest on oddalony o około 8,5 cm od górnego ekstremalnego włókna ściskanego.

Powyższe założenia (1 i 2) należy zweryfikować. Assumption 1 consists of calculating the strain in the compression steel (ε'_s) and comparing it with the yield strain (ε_y). If ε'_s is less than ε_y, our assumption is correct. Assumption 2 requires calculating the strain of the tensile steel reinforcement (ε_s) and comparing it to ε_y. If ε_s is greater than ε_y, then our assumption is correct. Weryfikujemy za pomocą obliczeń (nie pokazano), czy założenia 1 i 2 są prawidłowe.

Finally, to solve for the nominal moment (M_n), we set the sum of moments about the location of the concrete in compression (C_c) equal to zero. Można to zobaczyć na wykresie z rysunku 01.

Równanie to przyjmuje postać:

M_{n} = C'_{s} \cdot (\frac{a}{2} - d') + T_{s} \cdot (d - \frac{a}{2})

Wzór 3

Before we can solve for M_n, we must substitute C'_s and T_s for

A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot \frac{(C_{NA} - d')}{C_{NA}}

Wzór 4

and A_s ⋅ f_y, respectively.

Równanie ma postać:

M_{n} = A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot \frac{(C_{NA} - d')}{C_{NA}} \cdot (\frac{a}{2} - d') + A_{s} \cdot f_{y} \cdot (d - \frac{a}{2})

Wzór 5

We must also calculate a by multiplying β₁ and C_NA together before calculating M_n.

a = 4,66 in

By substituting these values into the M_n equation, we get the following:

M_{n} = 1.57 \cdot 29, 000 \cdot \frac{0.003 \cdot (5.83 - 2.5)}{5.83} \cdot (\frac{4.66}{2} - 3.0) + 4.71 \cdot 60 \cdot (20.5 - \frac{4.66}{2})

Formuła 6

Wartość Mn jest obliczana jako 5122,69 kip-in.

Na koniec, współczynnik bezpieczeństwa (φ) jest określany na podstawie tabeli 21.2.2 z ACI 318-14 [1]. Aby określić φ, odkształcenie przy rozciąganiu porównywane jest z odkształceniem granicznym 0,005. ε_t is equal to 0.00755 and is greater than 0.005. Belka posiada kontrolę rozciągania. Według tabeli 21.2.2 jest równe 0,90. When multiplying this factor by M_n, φM_n is equal to 4610.42 kip-in. Dlatego nośność belki przy zginaniu jest wystarczająca, aby wytrzymać przyłożony moment zginający.

φM_n > M_u = 4512.00 kip-in o.k.

Wytrzymałość na ścinanie

Uwaga: Wysokość użyteczna (d) do obliczeń projektowych dla ścinania jest przyjmowana jako 6 mm, w przeciwieństwie do 20,5 cm w opisie problemu. Miejsce maksymalnej siły tnącej jest jednocześnie miejscem, w którym znajduje się minimalny moment zginający (lico podpory). Aby skorelować obliczenia analityczne z wymiarowaniem zbrojenia w module RF-CONCRETE Members, moduł dodatkowy opiera efektywną wysokość na wymaganym zbrojeniu rozciąganym, a nie na zbrojeniu rozciąganym. Dlatego, przy minimalnym momencie zginającym na licu podpory, wymagana jest tylko jedna warstwa zbrojenia rozciąganego, biorąc pod uwagę głębokość efektywną 6 mm.

Na podstawie rozdz. 22.5.1.1 [1], we calculate the nominal shear strength (V_n) of the beam. Do obliczenia ścinania nominalnego stosuje się następujące równanie:
V_n = φ ⋅ (V_c + V_s)

Referencing Table 22.5.5.1 [1], concrete shear strength V_c is equal to the minimum of equations a, b, and c calculated in Sections 1, 2, and 3 below.

1. Równanie a ma postać:

V_{c - a} = (1.9 \cdot λ \cdot \sqrt{f'_{c}} 2, 500 \cdot ρ_{w} \cdot \frac{V_{u} \cdot d}{M_{u}}) \cdot b_{w} \cdot d, with λ = 1

Formuła 7

Mu występuje w odległości d od lica podpory (rozdział 9.4.3.2 [1]). Therefore, M_u is equal to 1533.38 kip-in. V_u = 61.10 kips.

ρ_{w} = \frac{A_{s}}{b_{w} \cdot d} = 0.01992

Formuła 8

V_c-a = 44.96 kips

Drugi Równanie b ma postać:

V_{c - b} = (1.9 \cdot λ \cdot \sqrt{f'_{c}} 2, 500 \cdot ρ_{w}) \cdot b_{w} \cdot d

Formuła 9

V_c-b = 46.26 kips

3. Równanie c ma postać:

V_{c - c} = 3.5 \cdot λ \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d

Formuła 10

V_c-c = 61.25 kips

Therefore, selecting the minimum value from the equations above, we find V_c is equal to 44.96 kips.

Na podstawie nominalnego ścinania z obliczeń betonu, minimalne zbrojenie na ścinanie jest znajdowane za pomocą Sec. 9.6.3 [1]. Here, if the required shear strength V_u is less than 0.5 ⋅ φ ⋅ V_c, then shear reinforcement is required.

V_u < 0.5 ⋅ φ ⋅ V_c
Gdzie,
φ = 0,75 (Tabela 21.2.1 [1])

Therefore, V_u = 61.10 kips > 16.86 kips. Stirrups are required.

Teoretyczny rozstaw jest określany na podstawie Sek. 9.5.1.1 [1]:
φ ⋅ V_n > V_u

We substitute (V_c + V_s) for V_n.

V_{s} > \frac{V_{u} - ϕ \cdot V_{c}}{ϕ}

Wzór 11

S_o, V_s > 36.51 kips.

Od rozdz. 22.5.10.5.3 [1], do obliczenia wymaganej wytrzymałości stali na ścinanie na ścinanie stosujemy następujące równanie:

V_{s} = \frac{A_{v} \cdot f_{yt} \cdot d}{s}

Wzór 12

Gdzie fyt jest granicą plastyczności stalowego zbrojenia rozciąganego, a d jest odległością od górnego włókna ściskanego do środka ciężkości zbrojenia rozciąganego.

Obliczono, że maksymalny rozstaw wynosi 14,79 cala. Zastosowano rozstaw 14 cali dla zbrojenia na ścinanie. Using a spacing of s = 14 inches, the above equation for steel shear strength, V_s, is calculated to be 38.57 kips.

Korzystając z tabeli 9.7.6.2.2 [1], należy określić maksymalny rozstaw ścinania. Aby określić, które równanie z tabeli 9.7.6.2.2 ma zastosowanie, należy użyć poniższego równania:

4 \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d = 4 \cdot \sqrt{5, 000 psi} \cdot 11 in \cdot 22.5 in = 70.29 kips

Formuła 13

The steel shear strength, V_s = 38.57 kips, is less than the calculated value of 70.00 kips. Referencing Table 9.7.6.2.2, the maximum shear spacing can be determined using the minimum value from the following calculations:

s_{\max} = \min (24, \frac{d}{2})

Wzór 14

Maksymalny rozstaw ścinania został wyznaczony na 11,25 cala. Wyznaczony wcześniej rozstaw ścinania przy użyciu prętów nr 4 rozmieszczonych co 14 cali nie jest wystarczający i należy zastosować zamiast niego 11 cali. Weryfikujemy, czy nominalna nośność na ścinanie jest większa niż wymagana wytrzymałość na ścinanie, aby mieć pewność, że zbrojenie na ścinanie i rozstaw są odpowiednie. With respect to our new max spacing of 11 inches, we receive a V_s value of 49.09 kips.

V_n = φ ⋅ (V_c + V_s) = 0.75 ⋅ (44.96 + 49.09) > V_u= 61.10 kips

Vn = 70,54 > 61,10 kips

Końcowa weryfikacja obejmuje sprawdzenie, czy wymiary przekroju są wystarczające, na podstawie Sek. 22.5.1.2. [1]. W tym celu porównuje się graniczną wytrzymałość na ścinanie z równ. 22.5.1.2 z ACI 318-14 [1]:

V_{u} ⩽ ϕ \cdot (V_{c} 8 \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d)

Wzór 15

This value of 105.04 kips is greater than V_u. Dlatego aktualne wymiary przekroju są wystarczające.

Wyniki

Alternatywą dla wymiarowania zbrojenia jest skorzystanie z modułu dodatkowego RF-/CONCRETE Members i przeprowadzenie obliczeń zgodnie z ACI 318-14 [1]. Moduł określa zbrojenie wymagane do przeniesienia obciążeń na belkę. Program oblicza również istniejące zbrojenie w oparciu o określone przez użytkownika rozmiary prętów, z uwzględnieniem wymagań dotyczących rozstawów określonych w normie. W tabeli wyników użytkownik ma możliwość wprowadzania niewielkich zmian w układzie zbrojenia rzeczywistego.

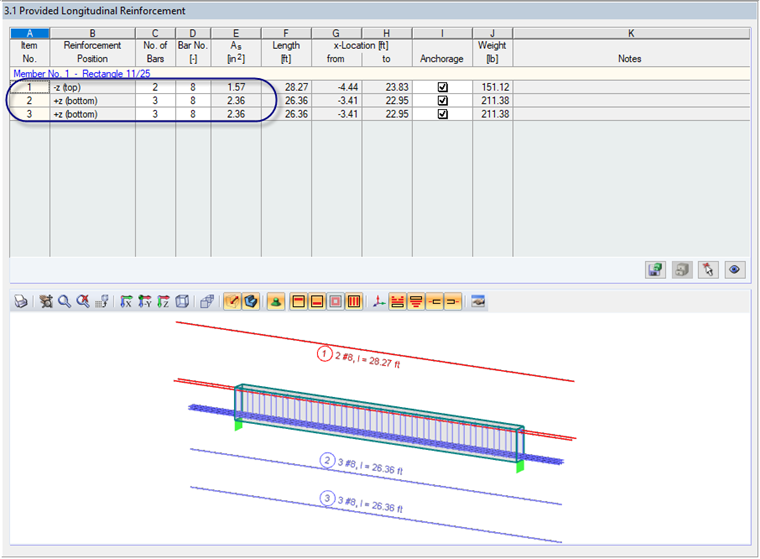
Based on the applied loads for this example, RF-CONCRETE Members has determined a required minimum tension reinforcement of 4.46 in² and a provided reinforcement of (6) #8 bars (A_s = 4.72 in²). This reinforcement layout is shown in Figure 02.

Zug- und Druckbewehrung RFEM-Diagramm

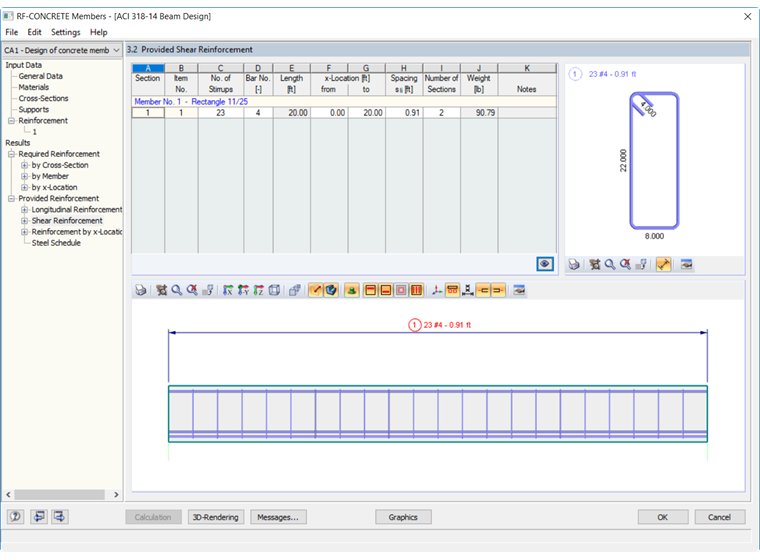
Wymagane zbrojenie na ścinanie pręta w ramach modułu RF-CONCRETE Members wyniosło 0,41 in²/ft. Aby spełnić to minimalne pole przekroju i zapewnić równomierny rozstaw strzemion na całej długości belki o długości 6 m, w programie zalecono zastosowanie prętów nr 4 w rozstawie 10,50 mm. Układ zbrojenia na ścinanie pokazano na rysunku 03.

Wykres RFEM dla metody Shear Reinforcement

Bügelbewehrung RFEM-Diagramm

Autor

Alex jest odpowiedzialny za szkolenie klientów, wsparcie techniczne i ciągły rozwój programów na rynek północnoamerykański.

Odnośniki

Oprogramowanie do analizy statyczno-wytrzymałościowej konstrukcji betonowych

Odniesienia

ACI 318-14, Wymagania norm budowlanych dotyczących betonu konstrukcyjnego i komentarz

Pobrane

Plik modelu w RFEM

1,35 MB

;