Bezeichnung
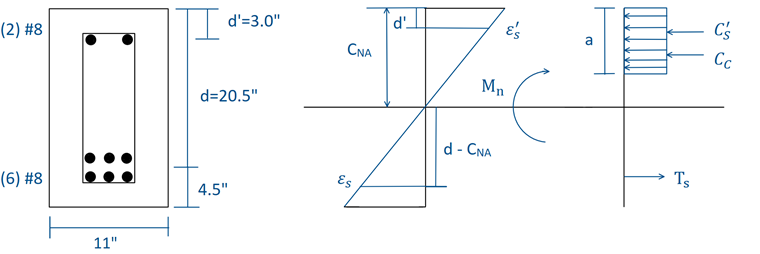
Für den doppelt bewehrten Balkenquerschnitt aus Stahlbeton, abgebildet in Bild 01, wird der Nachweis im Grenzzustand der Tragfähigkeit (ULS) nach ACI 318-14 [1] geführt, wobei LRFD-Lastkombinationen mit Beiwerten verwendet werden. Eine gleichförmige Eigenlast sowie Nutzlast von 2,0 kip/ft und 3,2 kip/ft ohne Beiwerte wird jeweils auf den Träger aufgebracht. Der gewählte rechteckige Balken hat einen Gesamtquerschnitt von 25 Zoll ⋅ 11 Zoll. Das Betonmaterial hat eine Druckfestigkeit (f'c) von 5.000 psi, während der Betonstahl eine Streckgrenze (fy) von 60.000 psi hat. Die Druckbewehrung (A's) besteht aus zwei Stäben der Nr. 8 mit einem Schwerpunktabstand (d') von 3,0 Zoll vom oberen Rand mit einer Gesamtfläche von 1,57 in². Die Zugbewehrung (As) besteht aus sechs Stäben der Nr. 8 mit einem Schwerpunktabstand (d) von 20,5 Zoll vom oberen Rand mit einer Gesamtfläche von 4,71 in². Die Schubbewehrung (Av) beinhaltet Bügel der Nr. 4 mit einer Gesamtfläche von 0,4 in². Die Abmessungen und das Spannungs-Dehnungs-Diagramm des Trägerquerschnitts sind in Bild 1 dargestellt.
Momentenfestigkeit
Das erforderliche Nennmoment Mu der aufgebrachten Lasten beträgt 4512,00 kip-in. Die folgenden Annahmen sind Voraussetzung, um die Gleichung zur Ableitung der Nennmomente zu erhalten.
Druckbewehrung fließt nicht: ε's < εy → f's = Es ⋅ ε's
Zugbewehrung fließt: εs ≥ εy → fs = fy
Mit der nachfolgenden Gleichung kann die Nulllinie bestimmt werden, nachdem das Spannungs-Dehnungs-Diagramm des Trägers untersucht wurde. Die Gleichung wird hergeleitet, indem die Druckkräfte gleich den Zugkräften gesetzt werden, um das Gleichgewicht zu erfüllen:
Ts = C's + Cc → As ⋅ fy - A's ⋅ f's - 0,85 ⋅ f'c ⋅ a ⋅ b = 0
Unter Verwendung des Dehnungsdiagramms und ähnlicher Dreiecke kann Folgendes angenommen werden:
Bekannt ist auch: a = β1 ⋅ CNA
Substituting β1 ⋅ CNA and
for a and ε's, respectively, into the equilibrium equation above, the neutral axis can be calculated, as all values are known except CNA.Using Table 22.2.2.4.3 from ACI 318 - 14 [1], β1 is equal to 0.80. Bei Auflösen der Gleichung nach CNA ergibt sich, dass der Wert ungefähr 5,83 Zoll vom oberen äußeren Rand entfernt ist.
Die oben genannten Annahmen (1 und 2) müssen verifiziert werden. Annahme 1 besteht darin, die Dehnung in der Druckbewehrung (ε's) zu berechnen und sie mit der Fließdehnung (εy) zu vergleichen. Wenn ε's kleiner als εy ist, dann ist die Annahme korrekt. Bei Annahme 2 muss die Berechnung der Dehnung der Zugbewehrung (εs) und der Vergleich mit εy erfolgen. Wenn εs größer ist als εy, ist die Annahme korrekt. Durch Berechnung (hier nicht gezeigt) wird verifiziert, dass die Annahmen 1 und 2 korrekt sind.
Um schließlich nach dem Nennmoment (Mn) aufzulösen, wird die Summe der Momente um die Stelle des druckbeanspruchten Betons (Cc) gleich null gesetzt. In Bild 1 ist das im Diagramm ersichtlich.
Die Gleichung lautet wie folgt:
Before we can solve for Mn, we must substitute C's and Ts for
and As ⋅ fy, respectively.Daraus ergibt sich folgende Gleichung:
Ebenso ist es erforderlich a zu berechnen, indem β1 und CNA zusammen multipliziert werden, bevor Mn berechnet wird.
a = 4,66 in
Setzt man diese Werte in die Mn-Gleichung ein, ergibt sich folgende Gleichung:
Mn wird berechnet mit 5122,69 kip-in.
Schließlich wird der Sicherheitsfaktor (φ) bestimmt, indem Tabelle 21.2.2 des ACI 318 -14 [1] herangezogen wird. Um φ zu bestimmen, wird die Zugdehnung mit der Bruchdehnung von 0,005 verglichen. εt ist gleich 0,00755 und damit größer als 0,005. Für den Balken ist Zugdehnung entscheidend (tension controlled). Anhand Tabelle 21.2.2 ergibt sich, dass φ gleich 0,90 ist. Wenn man diesen Faktor mit Mn multipliziert, ist φMn gleich 4610,42 kip-in. Daher ist die Tragfähigkeit des Balkens ausreichend, um dem einwirkenden Biegemoment standzuhalten.
φMn > Mu = 4512,00 kip-in o.k.
Schubfestigkeit
Hinweis: Die Nutzhöhe (d) für Berechnungen der Schubfestigkeit wird im Gegensatz zu den 20,5 inches, die in der Problemstellung definiert wurden, mit 22,5 inches angenommen. Die Position der maximalen Querkraft ist auch die Position des minimalen Biegungsmoments (Vorderseite des Auflagers). Um die analytischen Berechnungen in Zusammenhang mit der Bewehrungsbemessung in RF-BETON Stäbe zu setzen, basiert die Nutzhöhe im Zusatzmodul vielmehr auf der erforderlichen Zugbewehrung als auf der vorhandenen Zugbewehrung. Mit dem minimalen Biegungsmoment an der Auflagefläche ist deswegen nur eine Lage an Zugbewehrung erforderlich mit einer gegebenen Nutzhöhe von 22,5 inches.
Basierend auf Abs. 22.5.1.1 [1], we calculate the nominal shear strength (Vn) of the beam. Die folgende Gleichung wird zur Berechnung des Nominalschubs herangezogen:
Vn = φ ⋅ (Vc + Vs)
Referencing Table 22.5.5.1 [1], concrete shear strength Vc is equal to the minimum of equations a, b, and c calculated in Sections 1, 2, and 3 below.
1. Gleichung a lautet:
Mu tritt bei Vu auf, mit dem Abstand d von der Auflagerfläche (Abschnitt 9.4.3.2 [1]). Somit ist Mu gleich 1533,38 kip-in. Vu = 61,10 kips.
Vc-a = 44,96 kips
2. Gleichung b lautet:
Vc-b = 46,26 kips
3. Gleichung c lautet:
Vc-c = 61,25 kips
Anhand des kleinsten Wertes aus den obigen Gleichungen ergibt sich, dass Vc gleich 44,96 kips ist.
Gemäß des Nominalschubs der Betonberechnung ergibt sich die Mindestschubbewehrung aus Abschnitt 9.6.3 [1]. Wenn hier die erforderliche maximale Scherfestigkeit Vu kleiner als 0,5 ⋅ φ ⋅ Vc ist, dann ist eine Schubbewehrung erforderlich.
Vu < 0,5 ⋅ φ ⋅ Vc
Dabei ist
φ = 0,75 (Tabelle 21.2.1 [1])
Therefore, Vu = 61.10 kips > 16.86 kips. Stirrups are required.
Der theoretische Abstand wird anhand Abschnitt 9.5.1.1 [1] bestimmt:
φ ⋅ Vn > Vu
We substitute (Vc + Vs) for Vn.
So, Vs > 36.51 kips.
Aus Abschnitt 22.5.10.5.3 [1] wird die folgende Gleichung verwendet, um die erforderliche Scherfestigkeit für Stahl zu berechnen:
mit fyt als Streckgrenze der Zugbewehrung und d als Abstand vom oberen Rand zum Schwerpunkt der Zugbewehrung.
Der maximale Abstand (s) wird mit 14,79 inches berechnet. Ein Abstand von 14 inches wird für die Schubbewehrung verwendet. Bei Einsetzen von s = 14 inches in die obere Gleichung für die Schubfestigkeit von Stahl ergibt sich Vs = 38,57 kips.
Anhand von Tabelle 9.7.6.2.2 [1] ist der maximale Bügelabstand zu bestimmen. Die folgende Gleichung wird berechnet, um zu bestimmen, welche Gleichung in Tabelle 9.7.6.2.2 zutreffend ist:
The steel shear strength, Vs = 38.57 kips, is less than the calculated value of 70.00 kips. Referencing Table 9.7.6.2.2, the maximum shear spacing can be determined using the minimum value from the following calculations:
Der maximale Bügelabstand wird mit 11,25 inches berechnet. Der vorher bestimmte Bügelabstand von 14 inches mit den Stäben der Nr. 4 ist nicht ausreichend und 11 inches sollten stattdessen verwendet werden. Wir überprüfen, ob die Nennschubtragfähigkeit größer ist als die erforderliche Grenzschubfestigkeit, um sicherzustellen, dass die Schubbewehrung und der Abstand angemessen sind. Hinsichtlich des neuen maximalen Abstands von 11 inches ergibt sich ein Vs-Wert von 49,09 kips.
Vn = φ ⋅ (Vc + Vs) = 0,75 ⋅ (44,96 + 49,09) > Vu= 61,10 kips
Vn = 70,54 > 61,10 kips
Zur endgültigen Verifikation muss bestimmt werden, ob die Querschnittsabmessungen auf Basis des Abschnitts 22.5.1.2. [1] ausreichend sind. Dazu wird die maximale Scherfestigkeit mit Gleichung 22.5.1.2 aus ACI 318-14 [1] verglichen:
Dieser Wert von 105,04 kips ist größer als Vu. Daher sind die aktuellen Querschnittsabmessungen ausreichend.
Ergebnisse
Eine Alternative zur manuellen Ermittlung der Bewehrung ist die Verwendung des Zusatzmoduls RF-/BETON Stäbe und die Bemessung nach der Norm ACI 318-14 [1]. Das Modul bestimmt die erforderliche Bewehrung, um den einwirkenden Lasten am Balken standzuhalten. Darüber hinaus bemisst das Programm auch die vorhandene Bewehrung, die auf den Stabdurchmessern basiert, die vom Anwender definiert wurden, wobei die Normanforderungen bezüglich der Abstände berücksichtigt werden. Der Anwender kann kleine Anpassungen an die vorhandene Bewehrungsanordnung in der Ergebnistabelle vornehmen.
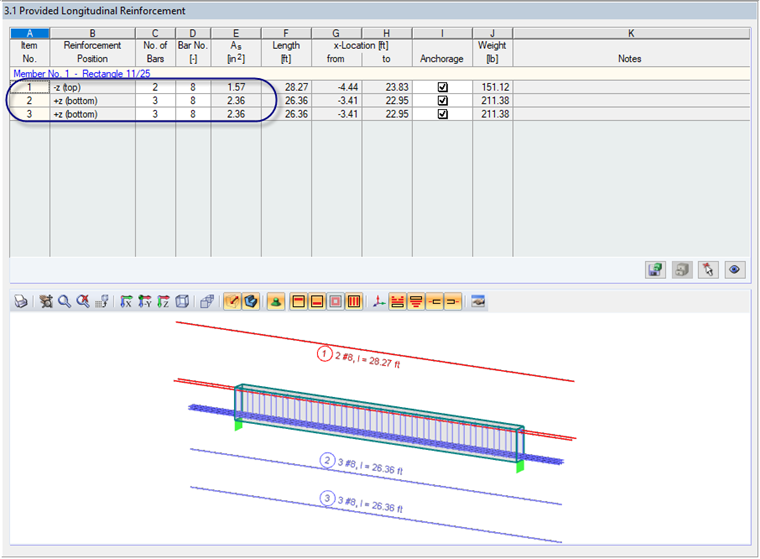
Based on the applied loads for this example, RF-CONCRETE Members has determined a required minimum tension reinforcement of 4.46 in² and a provided reinforcement of (6) #8 bars (As = 4.72 in²). This reinforcement layout is shown in Figure 02.
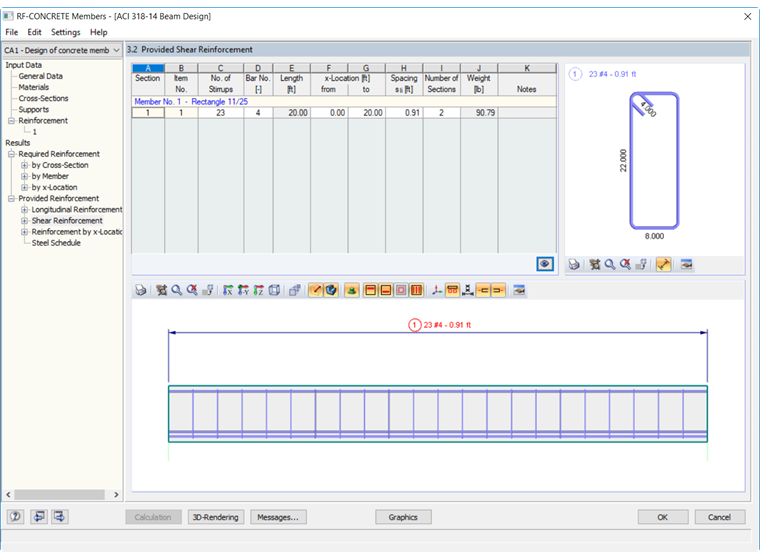
Die erforderliche Schubbewehrung für den Stab in RF-BETON Stäbe wird mit 0,41 in²/ft berechnet. Um diese Mindestfläche zu erreichen und um für einen gleichmäßigen Bügelabstand entlang des Balkens mit einer Länge von 20 ft zu sorgen, empfiehlt das Programm Stäbe der Größe 4 mit einem Abstand von 10,91 inches zu verwenden. Die Schubbewehrungsanordnung ist in Bild 03 dargestellt.