Descrizione
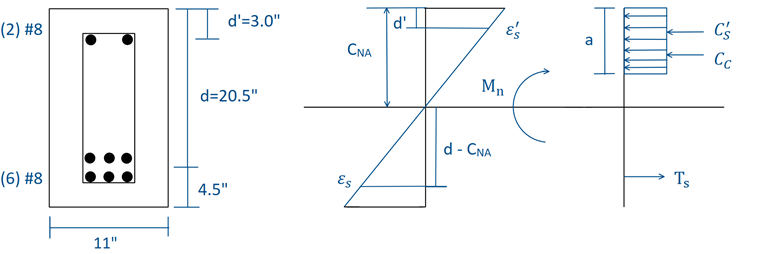
La sezione della trave in calcestruzzo armato doppia che si trova nella Figura 01 sarà progettata secondo SLU secondo ACI 318-14 [1] utilizzando combinazioni di carico LRFD fattorizzate. Alla trave vengono applicati un carico permanente uniforme non fattorizzato e un carico variabile di 2.0 kip/ft e 3.2 kip/ft, rispettivamente. La trave rettangolare selezionata ha una sezione trasversale complessiva di 25 pollici ⋅ 11 pollici. Il calcestruzzo ha una resistenza a compressione (f'c ) di 5.000 psi mentre l'acciaio di armatura ha una tensione di snervamento (fy ) di 60.000 psi. The compression reinforcement (A's) consists of two #8 bars with a centroid distance (d') of 3.0 inches from the top compression fiber with a total area of 1.57 in². The tensile reinforcement (As) consists of six #8 bars with a centroid distance (d) of 20.5 inches from the top compression fiber with a total area of 4.71 in². The shear reinforcement (Av) includes #4 stirrups for a total area of 0.4 in². Le dimensioni e il diagramma delle tensioni/deformazioni della sezione trasversale della trave sono mostrati nella Figura 01.
Resistenza al momento
The required nominal moment, Mu, from the applied loads is found to be 4512.00 kip-in. La derivazione dell'equazione per trovare il momento nominale richiede le seguenti ipotesi.
L'acciaio compresso non cede: ε's < εy → f's = Es ⋅ ε's
L'acciaio teso snerva: εs ≥ εy → fs = fy
Analizzando il diagramma delle tensioni e delle deformazioni della trave, l'asse neutro può essere trovato con l'equazione seguente. L'equazione si ottiene impostando le forze di compressione uguali alle forze di trazione al fine di soddisfare l'equilibrio:
Ts = C's + Cc → As ⋅ fy - A's ⋅ f's - 0.85 ⋅ f'c ⋅ a ⋅ b = 0
Utilizzando il diagramma di deformazione e triangoli simili, possiamo assumere:
Sappiamo anche: a = β1 ⋅ CNA
Substituting β1 ⋅ CNA and
for a and ε's, respectively, into the equilibrium equation above, the neutral axis can be calculated, as all values are known except CNA.Using Table 22.2.2.4.3 from ACI 318 - 14 [1], β1 is equal to 0.80. Risolvendo per CNA, troviamo che è uguale a circa 14 cm dalla fibra di compressione estrema superiore.
Le ipotesi di cui sopra (1 e 2) devono essere verificate. Assumption 1 consists of calculating the strain in the compression steel (ε's) and comparing it with the yield strain (εy). If ε's is less than εy, our assumption is correct. Assumption 2 requires calculating the strain of the tensile steel reinforcement (εs) and comparing it to εy. If εs is greater than εy, then our assumption is correct. Verifichiamo tramite il calcolo (non mostrato) che le ipotesi 1 e 2 sono valide.
Finally, to solve for the nominal moment (Mn), we set the sum of moments about the location of the concrete in compression (Cc) equal to zero. Questo può essere visto nel diagramma della Figura 01.
Questa equazione diventa:
Before we can solve for Mn, we must substitute C's and Ts for
and As ⋅ fy, respectively.L'equazione diventa:
We must also calculate a by multiplying β1 and CNA together before calculating Mn.
a = 11 cm
By substituting these values into the Mn equation, we get the following:
Mn è calcolato come 5122.69 kip-in.
Infine, il coefficiente di sicurezza (φ) è determinato facendo riferimento alla Tabella 21.2.2 da ACI 318 -14 [1]. Per determinare φ, la deformazione a trazione viene confrontata con la deformazione ultima di 0,005. εt is equal to 0.00755 and is greater than 0.005. La trave è controllata in trazione. Dalla tabella 21.2.2, φ è uguale a 0.90. When multiplying this factor by Mn, φMn is equal to 4610.42 kip-in. Pertanto, la capacità del momento della trave è sufficiente per resistere al momento flettente applicato.
φMn > Mu = 4512.00 kip-in o.k.
Resistenza a taglio
Nota: L'altezza efficace (d) per i calcoli di progetto a taglio è presa come 22,5 pollici contro i 20,5 pollici indicati nella dichiarazione del problema. La posizione della forza di taglio massima è anche la posizione del momento flettente minimo (faccia del vincolo esterno). Per correlare i calcoli analitici alla verifica dell'armatura in RF-CONCRETE Members, il modulo aggiuntivo basa l'altezza efficace sull'armatura tesa richiesta piuttosto che sull'armatura tesa fornita. Pertanto, con un momento flettente minimo sulla faccia del vincolo esterno, è necessario solo uno strato di armatura a trazione, data una profondità efficace di 50 cm.
Basato su Sez. 22.5.1.1 [1], we calculate the nominal shear strength (Vn) of the beam. La seguente equazione viene utilizzata per calcolare il taglio nominale:
Vn = φ ⋅ (Vc + Vs)
Referencing Table 22.5.5.1 [1], concrete shear strength Vc is equal to the minimum of equations a, b, and c calculated in Sections 1, 2, and 3 below.
1. L'equazione a è data come:
Mu si verifica a Vu che è a distanza d dalla faccia del vincolo esterno (Sezione 9.4.3.2 [1]). Therefore, Mu is equal to 1533.38 kip-in. Vu = 61.10 kips.
Vc-a = 44.96 kips
2. L'equazione b è data come:
Vc-b = 46.26 kips
3. L'equazione c è data come:
Vc-c = 61.25 kips
Therefore, selecting the minimum value from the equations above, we find Vc is equal to 44.96 kips.
Dopo il taglio nominale del calcolo del calcestruzzo, si trova l'armatura a taglio minima utilizzando Sez. 9.6.3 [1]. Here, if the required shear strength Vu is less than 0.5 ⋅ φ ⋅ Vc, then shear reinforcement is required.
Vu < 0.5 ⋅ φ ⋅ Vc
Dove,
φ = 0.75 (Tabella 21.2.1 [1])
Therefore, Vu = 61.10 kips > 16.86 kips. Stirrups are required.
La spaziatura teorica è determinata da Sez. 9.5.1.1 [1]:
φ ⋅ Vn > Vu
We substitute (Vc + Vs) for Vn.
So, Vs > 36.51 kips.
Dal sec. 22.5.10.5.3 [1], utilizziamo la seguente equazione per calcolare la resistenza a taglio dell'acciaio richiesta:
Dove, fyt è la tensione di snervamento dell'armatura in acciaio tesa e d è la distanza dalla fibra di compressione superiore al baricentro dell'armatura tesa.
La spaziatura massima è calcolata in 14,79 pollici. Viene utilizzata una spaziatura di 14 pollici per l'armatura a taglio. Using a spacing of s = 14 inches, the above equation for steel shear strength, Vs, is calculated to be 38.57 kips.
Utilizzando la Tabella 9.7.6.2.2 [1], è necessario determinare la spaziatura di taglio massima. La seguente equazione è calcolata per determinare quale equazione nella Tabella 9.7.6.2.2 è applicabile:
The steel shear strength, Vs = 38.57 kips, is less than the calculated value of 70.00 kips. Referencing Table 9.7.6.2.2, the maximum shear spacing can be determined using the minimum value from the following calculations:
La spaziatura di taglio massima è determinata in 11,25 pollici. La spaziatura di taglio determinata in precedenza con le barre nr. 4 distanziate a 14 pollici non è sufficiente e si dovrebbe invece utilizzare 11 pollici. Verifichiamo che la capacità di taglio nominale è maggiore della resistenza a taglio ultima richiesta per garantire che l'armatura a taglio e la spaziatura siano adeguate. With respect to our new max spacing of 11 inches, we receive a Vs value of 49.09 kips.
Vn = φ ⋅ (Vc + Vs) = 0.75 ⋅ (44.96 + 49.09) > Vu= 61.10 kips
Vn = 70,54 > 61,10 kip
La verifica finale include la determinazione se le dimensioni della sezione trasversale sono sufficienti in base alla Sez. 22.5.1.2. [1]. Per fare ciò, la resistenza a taglio ultima viene confrontata con l'Eqn. 22.5.1.2 da ACI 318-14 [1]:
This value of 105.04 kips is greater than Vu. Pertanto, le dimensioni attuali della sezione trasversale sono sufficienti.
Risultati
Un'alternativa per la verifica dell'armatura del calcestruzzo è quella di utilizzare il modulo aggiuntivo RF-/CONCRETE Members ed eseguire la verifica secondo ACI 318-14 [1]. Il modulo determinerà l'armatura necessaria per resistere ai carichi applicati sulla trave. Inoltre, il programma progetterà anche l'armatura fornita in base alle dimensioni delle barre specificate impostate dall'utente, tenendo conto dei requisiti di spaziatura dalla norma. L'utente ha l'opportunità di apportare piccole modifiche al layout dell'armatura fornito nella tabella dei risultati.
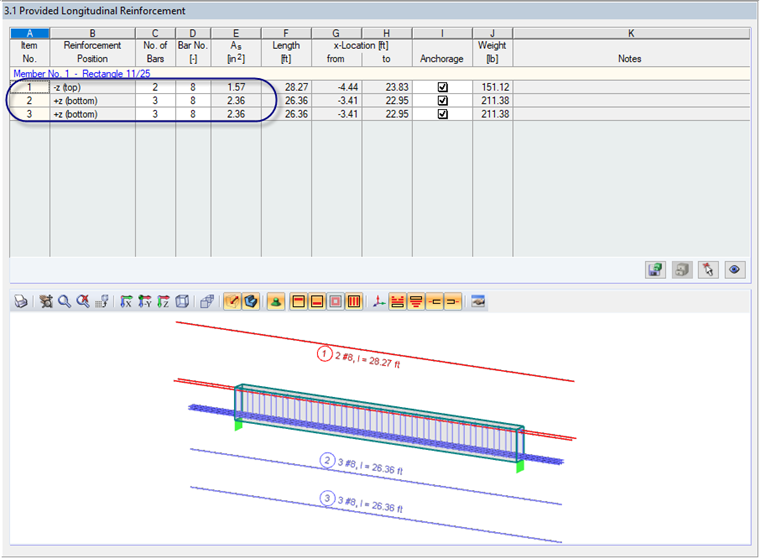
Based on the applied loads for this example, RF-CONCRETE Members has determined a required minimum tension reinforcement of 4.46 in² and a provided reinforcement of (6) #8 bars (As = 4.72 in²). This reinforcement layout is shown in Figure 02.
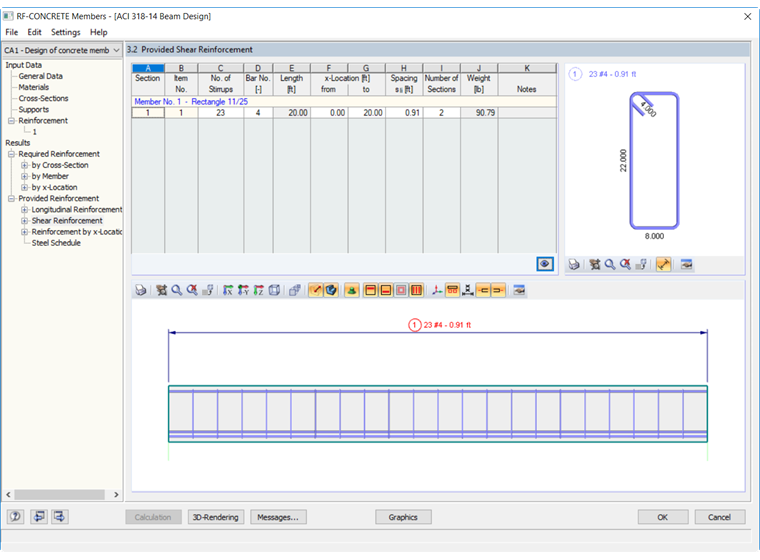
L'armatura a taglio richiesta per l'asta all'interno di RF-CONCRETE Members è stata calcolata in 0,41 in²/ft. Per soddisfare questa area minima e fornire una spaziatura uniforme delle staffe lungo la lunghezza della trave di 6 m, il programma ha raccomandato le barre nr. 4 con una spaziatura di 10,91 pollici. La disposizione dell'armatura a taglio è mostrata nella Figura 03.