Dimensionamento de vigas de betão armado segundo a norma ACI 318-14 no RFEM

Descrição

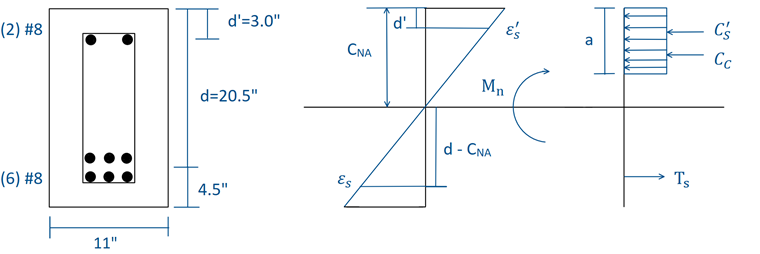
A secção da viga de betão duplamente armada na Figura 01 será dimensionada de acordo com a ULS de acordo com a norma ACI 318-14 [1] utilizando combinações de cargas LRFD fatoradas. Uma carga permanente uniforme não fatorizada e uma carga variável de 2,0 kip/ft e 3,2 kip/ft, respectivamente, são aplicadas à viga. A viga retangular selecionada tem uma secção total de 25 polegadas ⋅ 11 polegadas. O material de betão tem uma resistência à compressão (f'_c) de 5000 psi enquanto que a armadura de aço tem uma tensão de cedência (f_y) de 60 000 psi. A armadura de compressão (A'_s) é constituída por dois varões nº 8 com uma distância ao centro de gravidade (d') de 3,0 polegadas da fibra superior comprimida com uma área total de 1,57 mm². A armadura de tração (A_s ) é constituída por seis varões nº 8 com uma distância ao centro de gravidade (d) de 20,5 polegadas da fibra superior comprimida com uma área total de 4,71 in². A armadura de corte (A_v) inclui #4 estribos para uma área total de 0.4 pol². As dimensões e o diagrama de tensões/extensões da secção de viga é apresentado na Figura 01.

Stahlbetonquerschnitt: Spannungs-Dehnungs-Diagramm

Momento resistente

O momento nominal necessário, M_u, das cargas aplicadas é de 4512,00 kip-in. Derivar a equação para encontrar o momento nominal requer as seguintes suposições.

Aço de compressão não cede: ε'_s < ε_y → f'_s = E_s ⋅ ε'_s
O aço de tração cede: ε_s ≥ ε_y → f_s = f_y

Analisando o diagrama de tensões e de deformações da viga, o eixo neutro pode ser obtido com a equação abaixo. A equação é derivada através da definição das forças de compressão iguais às forças de tração de forma a satisfazer o equilíbrio:
T_s = C'_s + C_c → A_s ⋅ f_y - A'_s ⋅ f'_s - 0.85 ⋅ f'_c ⋅ a ⋅ b = 0

Utilizando o diagrama de extensões e triângulos semelhantes, pode-se assumir:

Também é do conhecimento: a = β₁ ⋅ C_NA

Substituindo β₁ ⋅ C_NA e

Utilizando a Tabela 22.2.2.4.3 do ACI 318 - 14 [1] , β₁ é igual a 0,80. Resolvendo para C_NA, descobre-se que é igual a cerca de 5,83 polegadas da fibra de compressão extrema superior.

As suposições acima (1 e 2) devem ser verificadas. A suposição 1 consiste no cálculo da deformação no aço de compressão (ε'_s) e na comparação com a deformação de cedência (ε_y). Se ε'_s é menor que ε_y, a nossa suposição está correta. A suposição 2 requer o cálculo da deformação da armadura de aço de tração (ε_s) e sua comparação com ε_y. Se ε_s é maior que ε_y , então a nossa suposição está correta. Verificamos através de um cálculo (não apresentado) que as suposições 1 e 2 são válidas.

Finalmente, para resolver para o momento nominal (M_n), definimos a soma dos momentos na posição do betão em compressão (C_c) igual a zero. Isto pode ser observado no diagrama da Figura 01.

Esta equação torna-se:

Antes de podermos resolver para M_n, temos de substituir C'_s e T_s 

A equação torna-se:

Também devemos calcular a multiplicando β₁ e C_NA antes de calcular M_n.

a = 4,66 in

Ao substituir esses valores na equação M_n, obtem-se o seguinte:

M_n é calculado com 5122.69 kip-in.

Por fim, o coeficiente de segurança (φ) é determinado tendo como referência a Tabela 21.2.2 do ACI 318 -14 [1]. Para determinar φ, a deformação por tração é comparada com a deformação de rotura de 0,005. ε_t é igual a 0,00755 e é maior que 0,005. A viga encontra-se controlada por tração. Da Tabela 21.2.2, φ é igual a 0,90. Quando multiplica este coeficiente por M_n, φM_n é igual a 4610,42 kip-in. Portanto, a capacidade de momento da viga é suficiente para resistir ao momento de flexão aplicado.

φM_n > M_u = 4512,00 kip-in ok

Resistência ao corte

Nota: A altura efetiva (d) para os cálculos de dimensionamento ao corte é assumida como 22,5 polegadas ao contrário das 20,5 polegadas estabelecida na descrição do problema. A localização da força de corte máxima é também a localização do momento de flexão mínimo (face do apoio). Para correlacionar os cálculos analíticos com o dimensionamento da armadura no RF-CONCRETE Members, o módulo adicional baseia-se na altura efetiva da armadura de tensão requerida em vez da armadura de tensão fornecida. Portanto, com momento fletor mínimo na face de apoio, é necessária apenas uma camada de armadura de tração, dada uma altura efetiva de 22,5 polegadas.

Com base na Secção 22.5.1.1 [1] , calcula-se a resistência de corte nominal (V_n) da viga. A seguinte equação é utilizada para calcular a força de corte nominal:
V_n = φ ⋅ (V_c + V_s)

Com base na Tabela 22.5.5.1 [1] , a resistência ao corte do betão V_c é igual ao mínimo das equações a, b e c calculada nas Secções 1, 2 e 3 abaixo.

1. A equação a é a seguinte:

   ${\mathrm{V}}_{\mathrm{c}-\mathrm{a}} = \left(1.9 · \mathrm{\lambda } · \sqrt{\mathrm{f}{\text{'}}_{\mathrm{c}}} 2,500 · {\mathrm{\rho }}_{\mathrm{w}} · \frac{{\mathrm{V}}_{\mathrm{u}} · \mathrm{d}}{{\mathrm{M}}_{\mathrm{u}}}\right) · {\mathrm{b}}_{\mathrm{w}} · \mathrm{d}, \mathrm{with} \mathrm{\lambda } = 1$

   Fórmula 7

   M_u ocorre em V_u que está a uma distância d da face de apoio (Secção 9.4.3.2 [1] ). Portanto, M_u é igual a 1533,38 kip-in. V_u = 61,10 kips

   ${\mathrm{\rho }}_{\mathrm{w}} = \frac{{\mathrm{A}}_{\mathrm{s}}}{{\mathrm{b}}_{\mathrm{w}} · \mathrm{d}} = 0.01992$

   Fórmula 8

   V_c-a = 44.96 kips

2. A equação b é dada como:

   ${\mathrm{V}}_{\mathrm{c}-\mathrm{b}} = \left(1.9 · \mathrm{\lambda } · \sqrt{\mathrm{f}{\text{'}}_{\mathrm{c}}} 2,500 · {\mathrm{\rho }}_{\mathrm{w}}\right) · {\mathrm{b}}_{\mathrm{w}} · \mathrm{d}$

   Fórmula 9

   V_c-b = 46.26 kips

3. A equação c é dada como:

   ${\mathrm{V}}_{\mathrm{c}-\mathrm{c}} = 3.5 · \mathrm{\lambda } · \sqrt{\mathrm{f}{\text{'}}_{\mathrm{c}}} · {\mathrm{b}}_{\mathrm{w}} · \mathrm{d}$

   Fórmula 10

   V_c-c = 61.25 kips

Portanto, selecionando o valor mínimo das equações acima, obtem-se que V_c é igual a 44,96 kips.

Após o cálculo de corte nominal do betão, a armadura de corte mínima é encontrada utilizando a Secção 9.6.3 [1] Aqui, se a resistência ao corte necessária V_u for inferior a 0,5 ⋅ φ ⋅ V_c, é necessária uma armadura de corte.

V_u < 0,5 ⋅ φ ⋅ V_c
Onde,
φ = 0,75 (Tabela 21.2.1 [1] )

Portanto, V_u = 61,10 kips > 16,86 kips. São necessários estribos.

O espaçamento teórico é determinado a partir da secção 9.5.1.1 [1] :
φ ⋅ V_n > V_u

Substitui-se (V_c + V_s ) por V_n.

Então, V_s > 36,51 kips.

Da secção 22.5.10.5.3 [1], utiliza-se a seguinte equação para calcular a resistência ao corte do aço necessária:

Onde, f_yt é a tensão de cedência da armadura em aço sob tracção e d é a distância da fibra de compressão superior ao centro geométrico da armadura de tensão.

O espaçamento máximo é calculado como 14,79 polegadas. É utilizado um espaçamento de 14 polegadas para a armadura de corte. Utilizando um espaçamento de s = 14 polegadas, a equação acima para a resistência ao corte do aço, V_s, é calculada como 38,57 kips.

Utilizando a Tabela 9.7.6.2.2 [1], deve ser determinado o espaçamento máximo de corte. A seguinte equação é calculada para determinar qual equação na Tabela 9.7.6.2.2 é aplicável:

A resistência ao corte do aço, V_s = 38,57 kips, é inferior ao valor calculado de 70,00 kips. Referenciando a tabela em 9.7.6.2.2, o espaçamento máximo de corte pode ser determinado utilizando o valor mínimo a partir dos cálculos seguintes:

O espaçamento de corte máximo é determinado como 28,759 mm. O espaçamento ao corte determinado anteriormente com os varões nº 4 com um espaçamento de 14 polegadas não é suficiente, devendo ser utilizado um espaçamento de 11 polegadas. Verifica-se que a resistência ao corte nominal é maior do que a resistência ao corte última necessária para garantir que a armadura de corte e o espaçamento são adequados. No que diz respeito ao nosso novo espaçamento máximo de 11 polegadas, obtem-se um valor V_s de 49,09 kips.

V_n = φ ⋅ (V_c + V_s ) = 0,75 ⋅ (44,96 + 49,09) > V_u = 61,10 kips

V_n = 70,54 > 61,10 kips

A verificação final inclui determinar se as dimensões da secção são suficientes com base na secção 22.5.1.2. [1] Para fazer isso, a resistência ao corte última é comparada com a Eq. 22.5.1.2 da ACI 318-14 [1] :

Este valor de 105,04 kips é maior que V_u. Portanto, as atuais dimensões da secção são suficientes.

Resultados

Uma alternativa para o dimensionamento das armaduras de betão é utilizar o módulo adicional RF-/CONCRETE Members e realizar o dimensionamento segundo a ACI 318-14 [1]. O módulo determinará a armadura necessária para resistir às cargas aplicadas na viga. Além disso, o programa também dimensionará a armadura fornecida com base nos tamanhos de barras especificados pelo utilizador, tendo em consideração os requisitos de espaçamento provenientes da norma. O utilizador tem a oportunidade de efetuar pequenos ajustes na disposição da armadura fornecida na tabela de resultados.

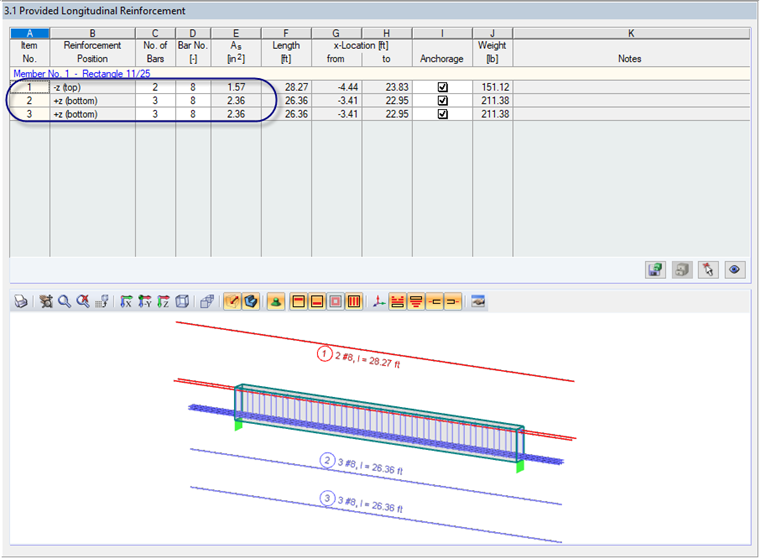
Com base nas cargas aplicadas para este exemplo, o RF-CONCRETE Members determinou uma armadura de tração mínima necessária de 4,46 in² e uma armadura fornecida de 8 varões de (6) (A_s = 4,72 in²). Esta disposição da armadura é apresentado na Figura 02.

Zug- und Druckbewehrung RFEM-Diagramm

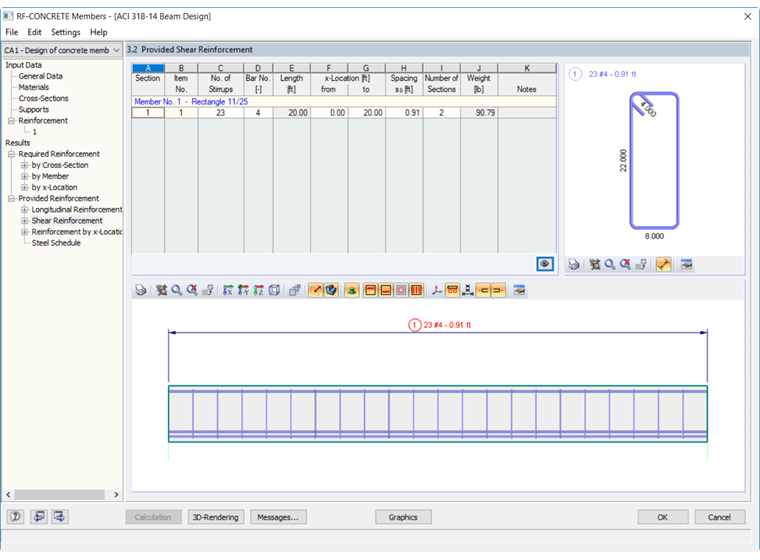
A armadura de corte necessária para a barra no RF-CONCRETE Members foi calculada como 0,41 in²/ft. Para atingir esta área mínima e proporcionar um espaçamento uniforme entre estribos ao longo do comprimento da viga de 6 m, o programa recomendou 4 varões com um espaçamento de 27,9 mm. A disposição da armadura de corte é apresentada na Figura 03.

Bügelbewehrung RFEM-Diagramm