Volver a la base de datos de conocimientos

20820x

001563

Alex Bacon, IET

2019-03-13

Cálculo de vigas de hormigón armado según ACI 318-14 en RFEM

RF-CONCRETE Members permite calcular las vigas de hormigón según ACI 318-14. Es importante calcular con precisión la tensión, compresión y la armadura de cortante de una viga por razones de seguridad. El siguiente artículo confirmará el cálculo de la armadura en RF-CONCRETE Members utilizando ecuaciones analíticas paso a paso según la norma ACI 318-14, que incluyen la resistencia a momento, la resistencia a cortante y la armadura necesaria. El ejemplo de viga de hormigón doblemente reforzado analizado incluye la armadura de cortante y se diseñará con el cálculo del estado límite último (ELU).

Descripción

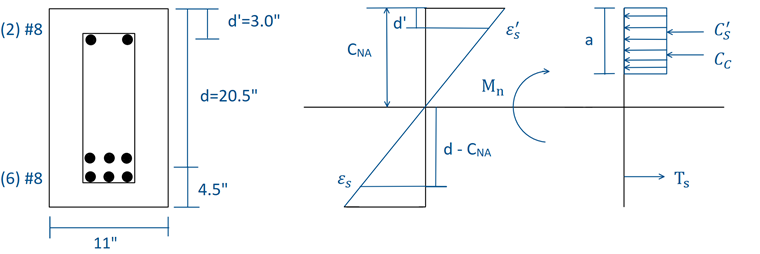
La sección de la viga de hormigón doblemente armado que se encuentra en la figura 01 se diseñará bajo el ELU según ACI 318-14 [1] utilizando combinaciones de carga LRFD factorizadas. Se aplica a la viga un peso propio uniforme sin factorizar y una carga viva de 2,0 kip/ft y 3,2 kip/ft, respectivamente. La viga rectangular seleccionada tiene una sección total de 25 pulgadas ⋅ 11 pulgadas. El material de hormigón tiene una resistencia a compresión (f'_c) de 5 000 psi, mientras que el acero de refuerzo tiene un límite elástico (f_y) de 60 000 psi. The compression reinforcement (A'_s) consists of two #8 bars with a centroid distance (d') of 3.0 inches from the top compression fiber with a total area of 1.57 in². The tensile reinforcement (A_s) consists of six #8 bars with a centroid distance (d) of 20.5 inches from the top compression fiber with a total area of 4.71 in². La armadura de cortante (A_v) incluye los estribos núm. 4 para un área total de 0,4 in². Las dimensiones y el diagrama de tensión/deformación de la sección de la barra se muestran en la figura 01.

Sección del hormigón armado: diagrama de tensiones y deformaciones

Stahlbetonquerschnitt: Spannungs-Dehnungs-Diagramm

Resistencia a momento

El momento nominal requerido, M_u, de las cargas aplicadas es 4512,00 kip-in. Se requieren las siguientes hipótesis para derivar la ecuación para obtener los momentos nominales.

El acero de compresión no tiene fluencia: ε'_s < ε_y → f'_s = E_s ⋅ ε'_s
El acero a tracción si tiene fluencia: ε_s ≥ ε_y → f_s = f_y

Al analizar el diagrama de tensiones y deformaciones de la viga, se puede encontrar el eje neutro con la siguiente ecuación. La ecuación se obtiene al establecer los esfuerzos de compresión iguales a los esfuerzos de tracción para alcanzar el equilibrio:
T_s = C'_s + C_c → A_s ⋅ f_y - A'_s ⋅ f'_s - 0.85 ⋅ f'_c ⋅ a ⋅ b = 0

Al utilizar el diagrama de deformaciones y triángulos similares, se puede suponer:

ε'_{s} = \frac{ε_{cu} \cdot (c_{NA} - d')}{c_{NA}}

Fórmula 1

También se sabe: a = β₁ ⋅ C_NA

Substituting β₁ ⋅ C_NA and

ε'_{s} = \frac{ε_{cu} \cdot (c_{NA} - d')}{c_{NA}}

Fórmula 1

for a and ε'_s, respectively, into the equilibrium equation above, the neutral axis can be calculated, as all values are known except C_NA.

A_{s} \cdot f_{y} - \frac{A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot (C_{NA} - d')}{C_{NA}} - 0.85 \cdot f'_{c} \cdot β_{1} \cdot C_{NA} \cdot b = 0

Fórmula 2

Using Table 22.2.2.4.3 from ACI 318 - 14 [1], β₁ is equal to 0.80. Resolviendo para CNA, encontramos que es igual a aproximadamente 5,83 pulgadas desde la fibra de compresión extrema superior.

Se deben verificar las hipótesis anteriores (1 y 2). La hipótesis 1 consiste en calcular la deformación en el acero de compresión (ε'_s) y compararla con la deformación de cedencia (ε_y). Si ε'_s es menor que ε_y, nuestra hipótesis es correcta. La hipótesis 2 requiere el cálculo de la deformación de la armadura de acero a tracción (ε_s) y la comparación con ε_y. Si ε_s es mayor que ε_y, entonces nuestra hipótesis es correcta. Verificamos mediante el cálculo (no mostrado) que los supuestos 1 y 2 son válidos.

Finalmente, para resolverlo para el momento nominal (M_n), establecemos que la suma de los momentos sobre la ubicación del hormigón sometido a compresión (C_c) igual a cero. Esto se puede ver en el diagrama de la figura 01.

Esta ecuación se convierte en:

M_{n} = C'_{s} \cdot (\frac{a}{2} - d') + T_{s} \cdot (d - \frac{a}{2})

Fórmula 3

Before we can solve for M_n, we must substitute C'_s and T_s for

A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot \frac{(C_{NA} - d')}{C_{NA}}

Fórmula 4

and A_s ⋅ f_y, respectively.

La ecuación se convierte en:

M_{n} = A'_{s} \cdot E_{s} \cdot ε_{cu} \cdot \frac{(C_{NA} - d')}{C_{NA}} \cdot (\frac{a}{2} - d') + A_{s} \cdot f_{y} \cdot (d - \frac{a}{2})

Fórmula 5

Antes de calcular M_n, también debemos calcular juntos β₁ y C_NA.

a = 4,66 in

Al sustituir estos valores en la ecuación M_n, se obtiene lo siguiente:

M_{n} = 1.57 \cdot 29, 000 \cdot \frac{0.003 \cdot (5.83 - 2.5)}{5.83} \cdot (\frac{4.66}{2} - 3.0) + 4.71 \cdot 60 \cdot (20.5 - \frac{4.66}{2})

Fórmula 6

Se calcula Mn como 5122,69 kip-in.

Finalmente, el coeficiente de seguridad (φ) se determina haciendo referencia a la tabla 21.2.2 de ACI 318-14 [1]. Para determinar φ, se compara la deformación por tracción con la deformación última de 0,005. ε_t es igual a 0,00755 y es mayor que 0,005. La tracción controla la viga. De la tabla 21.2.2, φ es igual a 0,90. Al multiplicar este factor por M_n, φM_n es igual a 4610,42 kip-in. Por lo tanto, la capacidad del momento de la viga es suficiente para resistir el momento flector aplicado.

φM_n > M_u = 4512.00 kip-in o.k.

Resistencia a cortante

Nota: El canto útil (d) para los cálculos de cálculo a cortante se toma como 56 cm en lugar de los 20,5 cm establecidos en el planteamiento del problema. La ubicación del esfuerzo cortante máximo también es la ubicación del momento flector mínimo (cara del apoyo). Para correlacionar los cálculos analíticos con el cálculo de la armadura en RF-CONCRETE Members, el módulo adicional basa la profundidad eficaz en la armadura de tracción requerida en lugar de la provista. Por lo tanto, con un momento flector mínimo en la cara del apoyo, solo se necesita una capa de armadura de tracción, con un canto útil de 560 mm.

Basado en la sec. 22.5.1.1 [1], we calculate the nominal shear strength (V_n) of the beam. La siguiente ecuación se usa para calcular la cortante nominal:
V_n = φ ⋅ (V_c + V_s)

Referencing Table 22.5.5.1 [1], concrete shear strength V_c is equal to the minimum of equations a, b, and c calculated in Sections 1, 2, and 3 below.

1. La ecuación a se da como:

V_{c - a} = (1.9 \cdot λ \cdot \sqrt{f'_{c}} 2, 500 \cdot ρ_{w} \cdot \frac{V_{u} \cdot d}{M_{u}}) \cdot b_{w} \cdot d, with λ = 1

Fórmula 7

Mu se produce en Vu, que está a una distancia d de la cara del apoyo (sección 9.4.3.2 [1]). Por lo tanto, M_u es igual a 1533,38 kip-in. V_u = 61,10 kips.

ρ_{w} = \frac{A_{s}}{b_{w} \cdot d} = 0.01992

Fórmula 8

V_c-a = 44,96 kips

2. La ecuación b se da como:

V_{c - b} = (1.9 \cdot λ \cdot \sqrt{f'_{c}} 2, 500 \cdot ρ_{w}) \cdot b_{w} \cdot d

Fórmula 9

V_c-b = 46,26 kips

3. La ecuación c se da como sigue:

V_{c - c} = 3.5 \cdot λ \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d

Fórmula 10

V_c-c = 61,25 kips

Por lo tanto, al seleccionar el valor mínimo de las ecuaciones anteriores, podemos ver que V_c es igual a 44,96 kips.

Siguiendo el cortante nominal del cálculo del hormigón, la armadura de cortante mínima se encuentra utilizando la sección 9.6.3 [1]. Here, if the required shear strength V_u is less than 0.5 ⋅ φ ⋅ V_c, then shear reinforcement is required.

V_u < 0.5 ⋅ φ ⋅ V_c
Donde,
φ = 0,75 (tabla 21.2.1 [1])

Therefore, V_u = 61.10 kips > 16.86 kips. Stirrups are required.

La separación teórica se determina a partir de la sec. 9.5.1.1 [1]:
φ ⋅ V_n > V_u

We substitute (V_c + V_s) for V_n.

V_{s} > \frac{V_{u} - ϕ \cdot V_{c}}{ϕ}

Fórmula 11

S_o, V_s > 36.51 kips.

A partir de la sección 22.5.10.5.3 [1], usamos la siguiente ecuación para calcular la resistencia a cortante requerida del acero:

V_{s} = \frac{A_{v} \cdot f_{yt} \cdot d}{s}

Fórmula 12

Donde, fyt es el límite elástico de la armadura de acero en tracción y d es la distancia desde la fibra de compresión superior al centro de gravedad de la armadura de tracción.

Las separaciones máximas se calculan en 14,79 pulgadas. Se usa una separación de 14 pulgadas para la armadura de cortante. Using a spacing of s = 14 inches, the above equation for steel shear strength, V_s, is calculated to be 38.57 kips.

Al utilizar la tabla 9.7.6.2.2 [1], se debe determinar el espaciado a cortante máximo. La siguiente ecuación se calcula para determinar qué ecuación de la tabla 9.7.6.2.2 se puede aplicar:

4 \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d = 4 \cdot \sqrt{5, 000 psi} \cdot 11 in \cdot 22.5 in = 70.29 kips

Fórmula 13

The steel shear strength, V_s = 38.57 kips, is less than the calculated value of 70.00 kips. Referencing Table 9.7.6.2.2, the maximum shear spacing can be determined using the minimum value from the following calculations:

s_{\max} = \min (24, \frac{d}{2})

Fórmula 14

Se determina que la separación máxima de cortante es de 11,25 pulgadas. La separación a cortante determinada previamente con barras núm. 4 espaciadas a 14 pulgadas no es suficiente, y en su lugar se debe usar 11 pulgadas. Verificamos que la capacidad a cortante nominal sea mayor que la resistencia a cortante última requerida para asegurar que la armadura de cortante y la separación sean adecuadas. With respect to our new max spacing of 11 inches, we receive a V_s value of 49.09 kips.

V_n = φ ⋅ (V_c + V_s) = 0.75 ⋅ (44.96 + 49.09) > V_u= 61.10 kips

Vn = 70,54 > 61,10 kips

La verificación final incluye determinar si las dimensiones de la sección son suficientes según la sección 22.5.1.2. [1]. Para hacer esto, se compara la resistencia última a cortante con la ecuación 22.5.1.2 de ACI 318-14 [1]:

V_{u} ⩽ ϕ \cdot (V_{c} 8 \cdot \sqrt{f'_{c}} \cdot b_{w} \cdot d)

Fórmula 15

Este valor de 105,04 kips es mayor que V_u. Por lo tanto, las dimensiones actuales de la sección son suficientes.

Resultados

Una alternativa para el cálculo de la armadura de hormigón es utilizar el módulo adicional RF-/CONCRETE Members y realizar el cálculo según ACI 318-14 [1]. El módulo determina la armadura necesaria para soportar las cargas aplicadas en la viga. Además, el programa también calcula la armadura proporcionada basándose en los tamaños de barra especificados definidos por el usuario, teniendo en cuenta los requisitos de espaciado de la norma. El usuario puede realizar pequeños ajustes en el cálculo de la armadura proporcionada en la tabla de resultados.

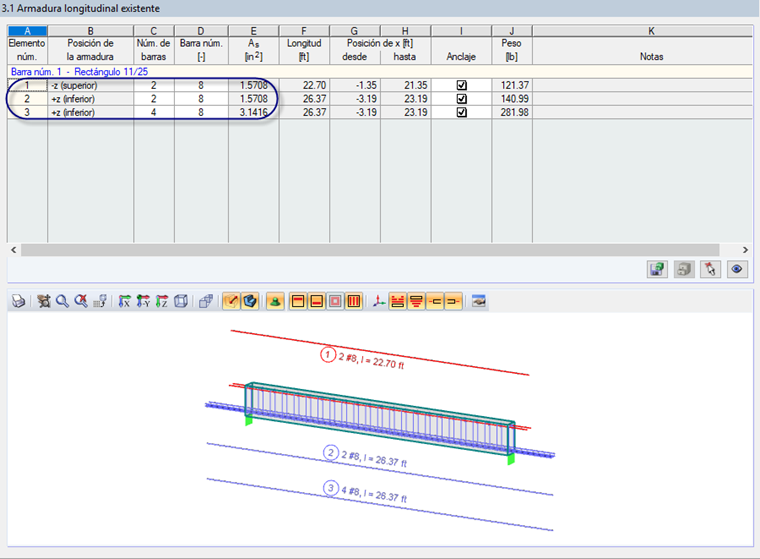
Based on the applied loads for this example, RF-CONCRETE Members has determined a required minimum tension reinforcement of 4.46 in² and a provided reinforcement of (6) #8 bars (A_s = 4.72 in²). This reinforcement layout is shown in Figure 02.

Diagrama RFEM de la armadura de tracción y compresión

Zug- und Druckbewehrung RFEM-Diagramm

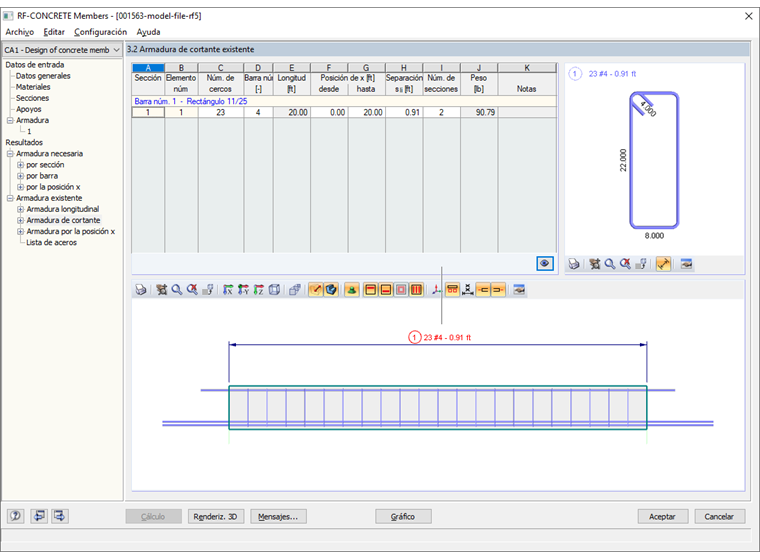
La armadura de cortante necesaria para la barra dentro de RF-CONCRETE Members se calculó en 0.41 in²/ft. Para cumplir con esta área mínima y proporcionar una separación uniforme de los cercos a lo largo de la viga de 20 pies, el programa ha recomendado barras #4 con una separación de 27 cm. La distribución de la armadura de cortante se muestra en la figura 03.

Bügelbewehrung RFEM-Diagramm

Autor

Alex es responsable de la formación de los clientes, el soporte técnico y el desarrollo continuo de programas para el mercado norteamericano.

Enlaces

Software de análisis y diseño para estructuras de hormigón

Referencias

ACI 318-14, Requisitos del código de construcción para hormigón estructural y comentarios

Descargas

Archivo del modelo de RFEM

1,35 MB

;