描述
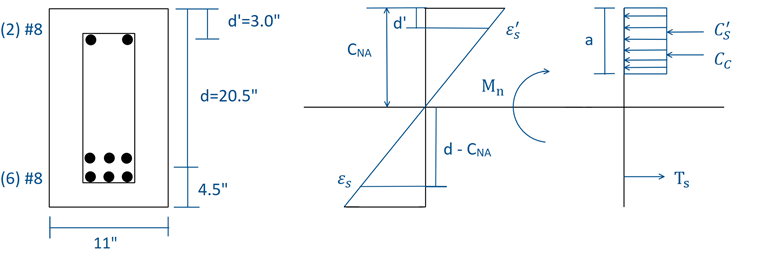
对于图 01 中所示的混凝土梁部分,在 ULS 条件下按照规范 ACI 318-14 [1] 使用设计后的 LRFD 荷载组合进行设计。 在梁上施加未调整的恒荷载和 3.2 大牛/立方米活荷载。 所选矩形梁的总截面为 25 英寸 ⋅ 11 英寸。 混凝土材料的抗压强度 (f'c ) 为 5000 psi,钢筋的屈服强度 (fy ) 为 60000 psi。 The compression reinforcement (A's) consists of two #8 bars with a centroid distance (d') of 3.0 inches from the top compression fiber with a total area of 1.57 in². The tensile reinforcement (As) consists of six #8 bars with a centroid distance (d) of 20.5 inches from the top compression fiber with a total area of 4.71 in². The shear reinforcement (Av) includes #4 stirrups for a total area of 0.4 in². 梁截面的尺寸和应力/应变图如图 01 所示。
抗弯强度
The required nominal moment, Mu, from the applied loads is found to be 4512.00 kip-in. 在推导计算公称弯矩的公式时,请作以下假设。
受压钢筋不屈服: ε's < εy → f's = Es ⋅ ε's
受拉钢筋屈服: εs ≥ εy → fs = fy
分析梁的应力应变曲线,可以使用下面的公式找到中性轴。 推导出该公式的公式为:
Ts = C's + Cc → As ⋅ fy - A's ⋅ f's - 0.85 ⋅ f'c ⋅ a ⋅ b = 0
根据应变图和相似三角形,我们可以假设:
我们还知道: a = β1 ⋅ CNA
Substituting β1 ⋅ CNA and
for a and ε's, respectively, into the equilibrium equation above, the neutral axis can be calculated, as all values are known except CNA.Using Table 22.2.2.4.3 from ACI 318 - 14 [1], β1 is equal to 0.80. 求解 CNA ,我们发现它距离最上部受压纤维大约 5.83 英寸。
以上假设(1 和 2)均需经过验证。 Assumption 1 consists of calculating the strain in the compression steel (ε's) and comparing it with the yield strain (εy). If ε's is less than εy, our assumption is correct. Assumption 2 requires calculating the strain of the tensile steel reinforcement (εs) and comparing it to εy. If εs is greater than εy, then our assumption is correct. 通过计算(未显示)可以证明假设 1 和 2 是成立的。
Finally, to solve for the nominal moment (Mn), we set the sum of moments about the location of the concrete in compression (Cc) equal to zero. 请参阅图 01。
上式变成:
Before we can solve for Mn, we must substitute C's and Ts for
and As ⋅ fy, respectively.公式变为:
We must also calculate a by multiplying β1 and CNA together before calculating Mn.
a = 4.66 英寸
By substituting these values into the Mn equation, we get the following:
Mn 计算为 5122.69 kip-in。
最后,根据规范 ACI 318 -14 [1] 中表 21.2.2 确定安全系数 (φ)。 为了确定 φ,需要将拉应变与极限应变 0.005 进行比较。 εt is equal to 0.00755 and is greater than 0.005. 杆件受拉控制。 从表 21.2.2 中得出,φ= 0.90。 When multiplying this factor by Mn, φMn is equal to 4610.42 kip-in. 因此,梁的抗弯承载力足以承受所施加的弯矩。
φMn > Mu = 4512.00 kip-in o.k.
抗剪强度
请注意: 用于剪力设计计算的有效高度 (d) 为 22.5 英寸,而不是问题陈述中的 20.5 英寸。 支座反力最大的地方,就是支座反力最小的地方(支座面) 为了在 RF-CONCRETE Members 中将解析计算与钢筋设计相关联,附加模块中的有效高度是基于实际需要的受拉钢筋而不是实配钢筋。 如果支座边缘弯矩最小,则只需要一层受拉钢筋,即有效深度为 22.5 厘米。
基于二分类 22.5.1.1 [1], we calculate the nominal shear strength (Vn) of the beam. 下面的公式用于计算名义剪力:
Vn = φ ⋅ (Vc + Vs)
Referencing Table 22.5.5.1 [1], concrete shear strength Vc is equal to the minimum of equations a, b, and c calculated in Sections 1, 2, and 3 below.
1. 公式 a 为:
Mu 出现在距离支座 Vu 远 d 的位置(章节 9.4.3.2 [1])。 Therefore, Mu is equal to 1533.38 kip-in. Vu = 61.10 kips.
Vc-a = 44.96 kips
2. 公式 b 为:
Vc-b = 46.26 kips
3. 公式 c 为:
Vc-c = 61.25 kips
Therefore, selecting the minimum value from the equations above, we find Vc is equal to 44.96 kips.
在计算混凝土的名义剪力之后,利用第 24 节找到最小抗剪钢筋。 9.6.3 [1] 。 Here, if the required shear strength Vu is less than 0.5 ⋅ φ ⋅ Vc, then shear reinforcement is required.
Vu < 0.5 ⋅ φ ⋅ Vc
这里,
φ = 0.75 (表 21.2.1 [1])
Therefore, Vu = 61.10 kips > 16.86 kips. Stirrups are required.
理论间距由 3.84 节确定。 9.5.1.1 [1]:
φ ⋅ Vn > Vu
We substitute (Vc + Vs) for Vn.
So, Vs > 36.51 kips.
从截面 根据 22.5.10.5.3 [1],我们使用以下公式来计算所需钢筋的抗剪强度:
式中 fyt 为受拉钢筋的屈服强度,d 为上部受压钢筋到受拉钢筋重心的距离。
计算得出的最大间距为 14.70 英寸。 抗剪钢筋的间距为 14 厘米。 Using a spacing of s = 14 inches, the above equation for steel shear strength, Vs, is calculated to be 38.57 kips.
采用表 9.7.6.2.2 [1] 必须确定最大剪切间距。 通过计算下列公式,以确定表 9.7.6.2.2 中的公式是适用的:
The steel shear strength, Vs = 38.57 kips, is less than the calculated value of 70.00 kips. Referencing Table 9.7.6.2.2, the maximum shear spacing can be determined using the minimum value from the following calculations:
最大剪切间距为 200 mm。 之前使用间隔为 14 英寸的 #4 钢筋确定的剪切间距是不够的,应使用 11 英寸。 我们要检查,名义抗剪承载力是否大于所需的极限抗剪强度,以便确保配置足够的抗剪钢筋和间距。 With respect to our new max spacing of 11 inches, we receive a Vs value of 49.09 kips.
Vn = φ ⋅ (Vc + Vs) = 0.75 ⋅ (44.96 + 49.09) > Vu= 61.10 kips
Vn = 70.54 > 61.10 kips
最终的验算包括确定截面尺寸是否足够。 22.5.1.2. [1]。 为此,将极限抗剪强度与公式 2进行比较。 ACI 318-14 [1] 22.5.1.2:
This value of 105.04 kips is greater than Vu. 因此,当前截面尺寸已经足够。
结果
进行钢筋混凝土设计的另一个选择是使用附加模块 RF-/CONCRETE Members,然后按照规范 ACI 318-14 [1] 进行设计。 模块将确定承受梁上的荷载所需的配筋。 此外,程序还会根据用户设置的钢筋尺寸考虑规范中的间距要求进行配筋计算。 用户可以在结果表中对钢筋布置进行小的调整。
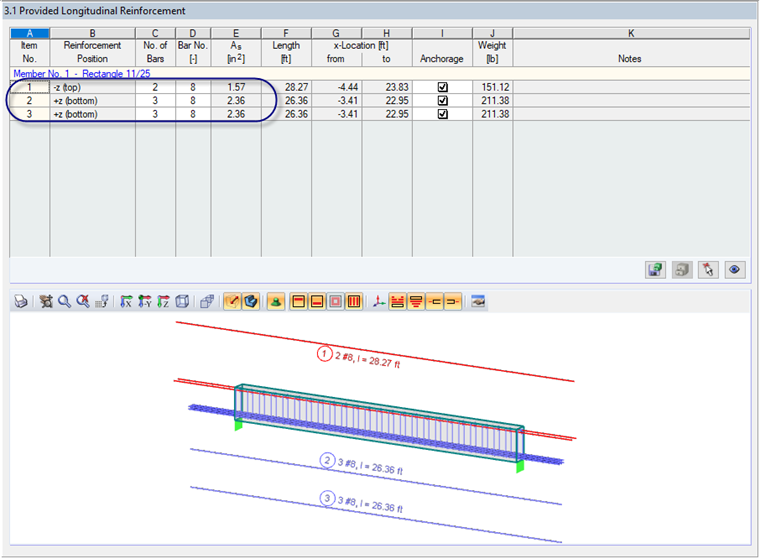
Based on the applied loads for this example, RF-CONCRETE Members has determined a required minimum tension reinforcement of 4.46 in² and a provided reinforcement of (6) #8 bars (As = 4.72 in²). This reinforcement layout is shown in Figure 02.
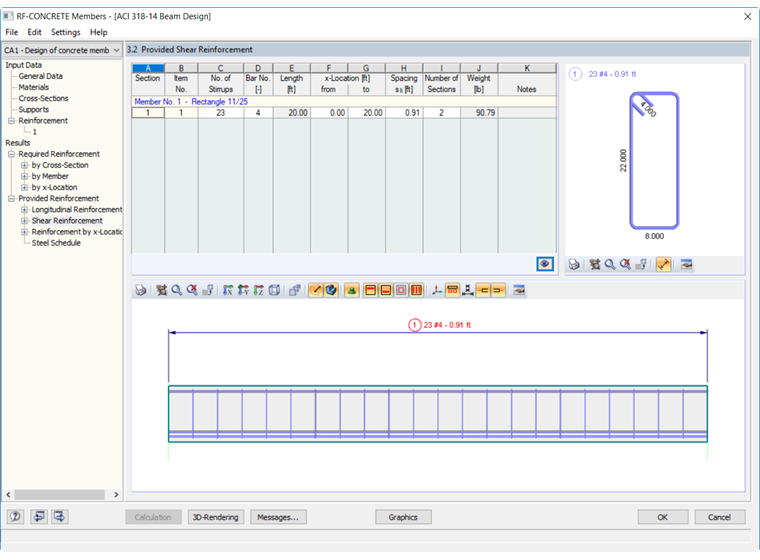
在 RF-CONCRETE Members 中该杆件所需的抗剪配筋为 0.41 in²/ft。 为了满足这个最小面积的要求,并为 20 米长的梁提供均匀的箍筋间距,程序建议 #4 根钢筋的间距为 10.91 英寸。 抗剪配筋如图 03 所示。