Различия в расчете моментов инерции у соединенных и несвязанных частичных сечений

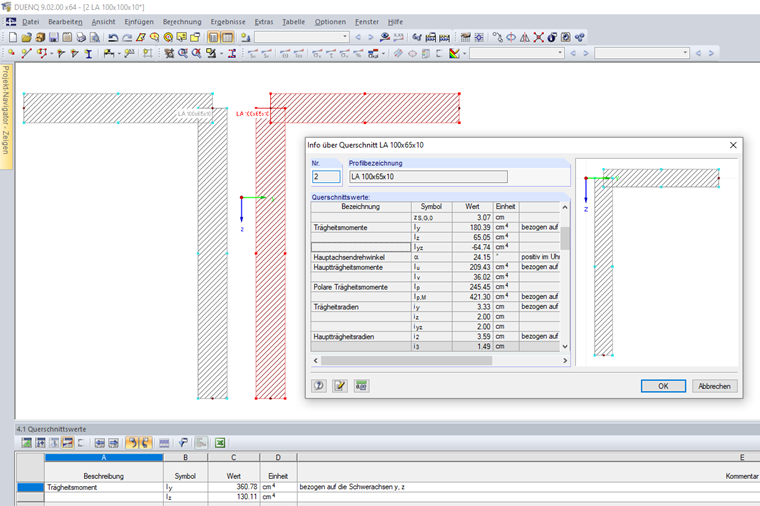
Если сечение состоит из нескольких несоединенных частичных профилей, то сумма моментов инерции рассчитывается без учета компонентов теоремы Штейнера. Сечение, показанное на Рисунке 01, состоит из двух уголков, которые не соединены друг с другом.

1 Сечение, состоящее из нескольких не связанных частичных сечений

Отдельные уголки имеют следующие моменты инерции:
I_y,1,2 = 180,39 см⁴ (относительно осей центра тяжести y, z)
I_z,1,2 = 65,05 см⁴ (относительно осей центра тяжести y, z)

Моменты инерции всего сечения равны:
I_y,1+2 = 2 ⋅ I_y,1,2 = 2 ⋅ 180,39 = 360,78 см⁴ (относительно осей центра тяжести y, z)
I_z,1+2 = 2 ⋅ I_z,1,2 = 2 ⋅ 65,05 = 130,11 см⁴ (относительно осей центра тяжести y, z)

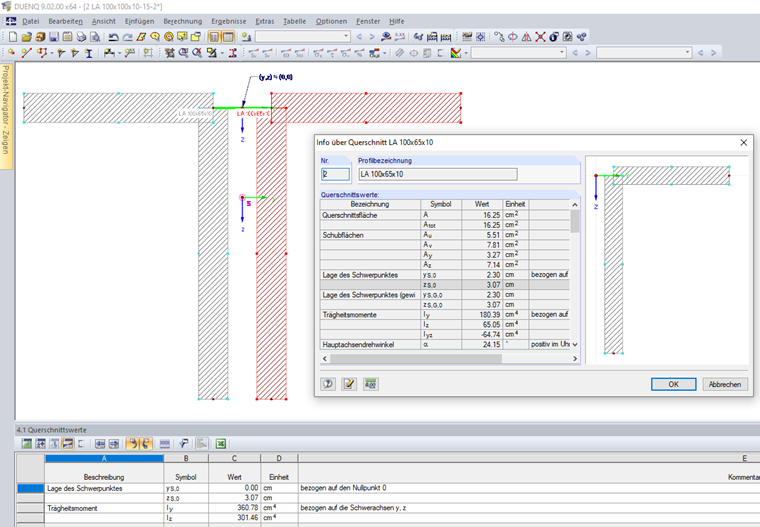
Если сечение состоит из нескольких соединенных частичных профилей, то сумма моментов инерции рассчитывается с помощью компонентов теоремы Штейнера. Сечение, показанное на Рисунке 02, состоит из двух соединенных уголков.

2 Сечение, состоящее из нескольких соединенных частичных сечений

Отдельные уголки имеют следующие характеристики сечения:
A_1,2 = 16,25 см²
y_S,0,1,2 = ±2,30 см (относительно нулевой точки)
z_S,0,1,2 = 3,07 см (относительно нулевой точки)
I_y,1,2 = 180,39 см⁴ (относительно осей центра тяжести y, z)
I_z,1,2 = 65,05 см⁴ (относительно осей центра тяжести y, z)

Характеристики сечения всего сечения включают в себя:
y_S,0,1+2 = 0,00 см (относительно нулевой точки)
z_S,0,1+2 = 3,07 см (относительно нулевой точки)
I_y,1+2 = 2 ⋅ I_y,1,2 + 2 ⋅ A_1,2 ⋅ (z_S,0,1,2 - z_S,0,1+2 )²
I_y,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 - 3,07)² = 360,78 см⁴ (относительно осей центра тяжести y, z)
I_z,1+2 = 2 ⋅ I_z,1,2 + 2 ⋅ A_1,2 ⋅ (y_S,0,1,2 - y_S,0,1+2 )²
I_z,1+2 = 2 ⋅ 65,05 + 2 ⋅ 16,25 ⋅ (2,30 - 0,00)² = 301,46 см⁴ (относительно осей центра тяжести y, z)