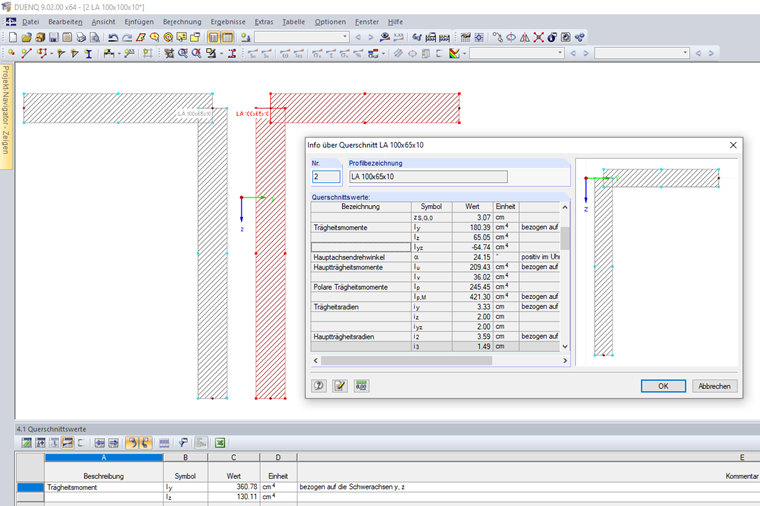
Si la sección consta de varias secciones parciales no conectadas , la suma de los momentos de inercia se calcula sin los componentes del teorema de los ejes paralelos. La sección que se muestra en la figura 01 consta de dos secciones angulares que no están conectadas entre sí.
Las secciones angulares individuales tienen los siguientes momentos de inercia:
Iy,1,2 = 180.39 cm4 (referido a los ejes del centro de gravedad y, z)
Iz,1,2 = 65.05 cm4 (referido a los ejes del centro de gravedad y, z)
Los momentos de inercia de toda la sección dan como resultado:
Iy,1+2 = 2 ⋅ Iy,1,2 = 2 ⋅ 180,39 = 360,78 cm4 (referido a los ejes del centro de gravedad y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 = 2 ⋅ 65,05 = 130,11 cm4 (referido a los ejes del centro de gravedad y, z)
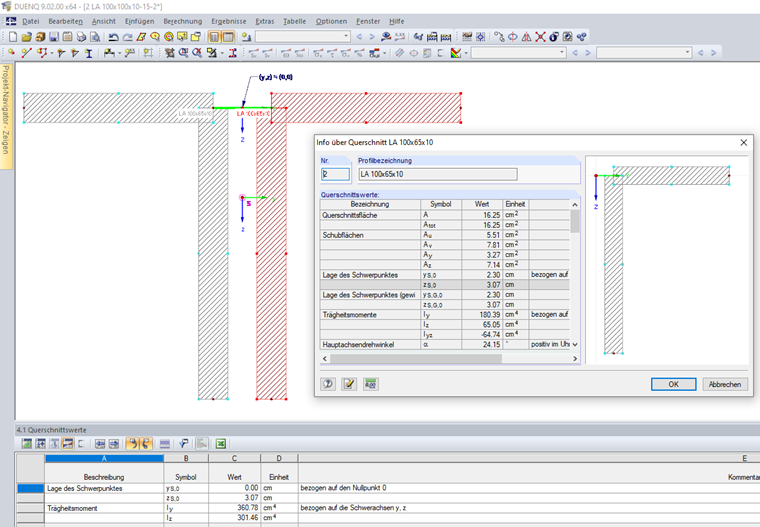
Si la sección consta de varias secciones parciales conectadas , la suma de los momentos de inercia se calcula con los componentes del teorema de los ejes paralelos. La sección que se muestra en la figura 02 consta de dos secciones angulares conectadas.
Las secciones angulares individuales tienen las siguientes propiedades de sección:
A1,2 = 16,25 cm²
yS,0,1,2 = ±2.30 cm (referido al punto cero)
zS,0,1,2 = 3,07 cm (referido al punto cero)
Iy,1,2 = 180.39 cm4 (referido a los ejes del centro de gravedad y, z)
Iz,1,2 = 65.05 cm4 (referido a los ejes del centro de gravedad y, z)
Las propiedades de la sección de toda la sección dan como resultado:
yS,0,1+2 = 0.00 cm (referido al punto cero)
zS,0,1+2 = 3,07 cm (referido al punto cero)
Iy,1+2 = 2 ⋅ Iy,1,2 + 2 ⋅ A1,2 ⋅ (zS,0,1,2 - zS,0,1+2 )²
Iy,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 - 3,07)² = 360,78 cm4 (referido a los ejes del centro de gravedad y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 + 2 ⋅ A1,2 ⋅ (yS,0,1,2 - yS,0,1+2 )²
Iz,1+2 = 2 ⋅ 65,05 + 2 ⋅ 16,25 ⋅ (2,30 - 0,00)² = 301,46 cm4 (referido a los ejes del centro de gravedad y, z)